Effects of chemical reaction and heat generation on double-diffusive natural convection along a non-isothermal vertical cone in non-newtonian fluid saturated porous medium with variable viscosity and thermal radiation

M.A.A. Mahmoud

Department of Mathematics, Faculty of Science,
Benha University (13518), Egypt
mostafabdelhameed@yahoo.com

Abstract— In this work, we studied of variable viscosity, Dufour and Soret effects on free convection heat and mass transfer of a non- Newtonian power-law fluid over a vertical full cone in a saturated porous medium in the presence of chemical reaction, non uniform heat generation and thermal radiation. The transformed nonlinear ordinary differential equations are solved numerically using the fourthorder Runge-Kutta method coupled with the shooting method. The influences of various parameters on the local Nusselt number and the local Sherwood number are presented and discussed.

Keywords— Dufour And Soret Effects; Non-newtonian Power-law Fluids; Variable Viscosity; Thermal Radiation; Porous Medium; Chemical Reaction; Heat Generation.

I. INTRODUCTION

Considerable attention by many authors on the problem of combined heat and mass transfer convection in a fluid saturated porous medium has been made because of its practical applications such as heat exchangers devices, petroleum reservoirs, underground spreading of chemical contaminants through water saturated soil, nuclear waste disposal, chemical catalytic reactors and moisture migration in fibrous insulation. The boundary layer analysis about variable viscosity effects on the double-diffusive convection near a vertical truncated cone in a fluid-saturated porous medium with constant wall temperature and concentration was investigated by Cheng (2009a). Yih (1999) studied heat and mass transfer driven by natural convection from a truncated cone immersed in a porous medium with variable heat and mass flux or with constant wall temperature and concentration. Natural convection heat transfer of a Darcian fluid about a cone was investigated by Cheng et al. (1985). Free convection boundary layer over a vertical surface immersed in a porous medium with constant heat and mass fluxes taking into account the effect of wall injection was analyzed by Lai and Kulacki (1991).

The above studies were restricted to Newtonian fluids, while many fluids involved in a number of processes that occur in chemical industry display non- Newtonian fluid behavior. Relationship between shear stress and shear rate for non-Newtonian fluids is different from that Newtonian fluids. Many of non- Newtonian fluids used in chemical engineering follow the Ostwald- de Waele power-law model for the shear stress. Buoyancy-induced flow of non-Newtonian fluids in a porous medium over a vertical plate with nonuniform surface heat flux was investigated by Mehta and Rao (1994). Kumari and Jayanthi (2005) investigated the influence of a uniform lateral mass flux on the natural convection flow past a vertical cone embedded in a porous medium saturated with non- Newtonian fluid. The influence of uniform lateral mass flux on the natural convection of non-Newtonian power-law fluids on an isothermal or isoflux vertical cone in a porous medium was studied by Yih (1998). The problem of steady free convection boundary layer over a vertical cone embedded in a porous medium filled with a non-Newtonian fluid in the presence of internal heat generation was investigated by Gro¸san et al. (2004). Cheng (2009b) investigated the problem of the steady natural convection boundary layer flow over a downward pointing vertical cone in porous media saturated with non-Newtonian power-law fluids under mixed thermal boundary conditions.

In the above mentioned works, Soret (thermaldiffusion) and Dufour (diffusion-thermo) effects are not taken into consideration. Such effects are significant when density differences exist in the flow regime. For example when species are introduced at a surface in fluid domain, with different (lower) density than the surrounding fluid, both Soret and Dufour effects can be significant. Bêg et al. (2009) examined the combined effects of Soret and Dufour on magnetohydrodynamic heat and mass transfer from a vertical stretching surface in a Darcian porous medium under uniform magnetic field. A steady two-dimensional magnetohydrodynamic free convection flow viscous dissipating fluid past a semi-infinite moving vertical plate in a porous medium with Soret and Dufour effects was analyzed by Reddy and Reddy (2010). Tai and Char (2010) investigated Soret and Dufour effects on free convection flow of non-Newtonian fluids along a vertical plate immersed in a porous medium in the presence of thermal radiation. The influences of Dufour and Soret on mixed convection flow past a vertical porous flat plate embedded in a porous medium have been studied by Alam and Rahman (2006). Recently, Cheng (2009c) investigated the Soret and Dufour effects on heat and mass transfer over a vertical cone in a porous medium with constant wall temperature and concentration. The effects of Soret and Dufour on heat and mass transfer over a vertical cone embedded in a porous medium with constant heat and mass fluxes were examined by Cheng (2011).

The literature survey shows that the influence of chemical reaction and non-uniform heat generation on the steady free convection boundary layer heat and mass transfer adjacent to a non-isothermal vertical full cone embedded in a porous medium filled with a non-Newtonian power-law fluid in the presence of variable viscosity, thermal radiation, Dufour and Soret effects have not been studied. The aim of the present work is to study the effects of Dufour, Soret, chemical reaction and heat generation on free convection heat and mass transfer from a non-isothermal vertical full inverted cone with variable wall temperature and concentration in a porous medium saturated with a non-Newtonian power-law fluid in the presence of variable viscosity and thermal radiation. Applications of this problem can be found in many engineering problems. For example a drilling bit as used in oil drilling applications.

II. FORMULATION OF THE PROBLEM

Let us consider the flow in a porous medium saturated filled with a non-Newtonian power-law fluid over a non-isothermal vertical full cone. Under the Boussinesq and the boundary layer approximations, the governing equations can be written as Cheng (2009c):

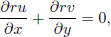	(1)
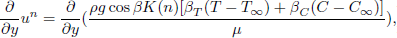	(2)
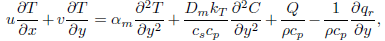	(3)
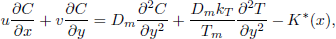	(4)

where r = xsinβ is the cone radius, x and y are the Cartesian coordinates along and normal to the cone generator. The flow situation being considered here is shown in Fig. 1. Here u and v are the components of the velocity in x and y directions, respectively. n is the power-law index . The fluids for which n < 1 are called pseudoplastic fluids, the fluids for which n > 1 are called dilatant fluids and the fluids for which n = 1 are called Newtonian fluids. g is the gravitational acceleration, µ is the consistency coeffcient, c_p is the specific heat at constant pressure, ρ is the density of the fluid, T_∞ is the temperature at infinity, T is the temperature of the fluid, α_m is the effective thermal diffusivity, D_m is the mass diffusivity, K(n) is the modified permeability, β_T and β_C are the coeffcients for thermal expansion and concentration expansion, respectively, k_T is the thermal diffusion ratio and T_m is the mean fluid temperature. Q(x) is the volumetric rate of heat generation/absorption and K^*(x) is the chemical reaction rate.

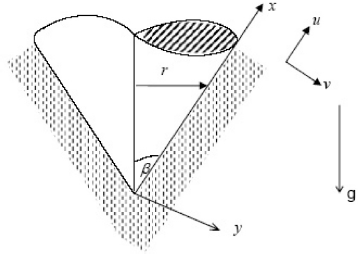
Figure 1: Physical Model and Coordinate System.

The boundary conditions are:

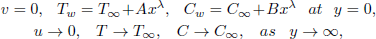(5)

where A, B are positive constants and λ is the power index of the wall temperature and concentration.

Using Rosseland approximation Raptis (1999), The radiative heat flux q_r is :

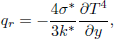(6)

where σ^* is the Stefan-Boltzmann constant and k^* is the mean absorption coefficient. Following Raptis (1999), we assume that the temperature difference within the flow are small such that T⁴ may be expressed as a linear function of the temperature. Expanding T⁴ in a Taylor series about T_∞ and neglecting higher-order terms, we have:

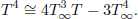(7)

Now Eq.(3) becomes:

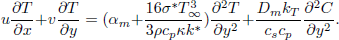(8)

Introducing the similarity variable employed earlier by GroŞan et al. (2004) gives:

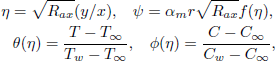(9)

where ψ is the stream function that satisfies the continuity Eq. (1) defined by:

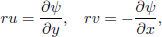(10)

and R_ax is the generalized local Rayleigh number for a porous medium, which is defined as:

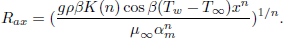(11)

In order that similarity solutions of Eqs. (1)-(4) exist it is assumed that the heat generation Q(x) and the chemical reaction K^*(x) are given in the following form:

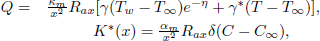(12)

where κ_m is the effective thermal conductivity, γ and γ^* are the coefficient of space-and temperature dependent internal heat generation/absorbtion, respectively. γ > 0 and γ^* > 0 corresponds to internal heat generation, while γ < 0 and γ^* < 0 corresponds to internal heat absorption and δ is the destructive chemical reaction parameter (> 0) or constructive chemical reaction parameter (< 0).

The coefficient of viscosity µ(θ) was assumed to obey the Reynolds viscosity model (Bagai, 2004):

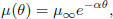(13)

where α is a dimensionless viscosity parameter depending on the nature of the fluid and µ_∞ is the ambient coefficient of consistency.

In view of Eqs. (9) and (12), the Eqs. (2),(8) and (4) reduce to:

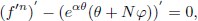	(14)
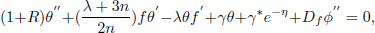	(15)
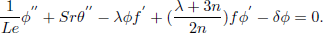	(16)

The boundary conditions take the form:

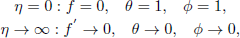(17)

where 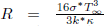is the radiation parameter, 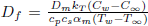is the Dufour parameter, 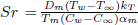is the Soret parameter, 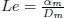is the Lewis number and 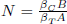is the buoyancy ratio.

It is observed that for α = 0 (constant viscosity), R = 1 (no radiation interaction), γ = γ^* = 0 (without heat generation) λ = 0 (constant wall temperature and concentration) and n = 1 (Newtonian case), Eqs. (14)-(16) reduce to those of Cheng (2009c).

Important physical parameters of interest in this problem are the local Nusselt number and the local Sherwood number which are given by:

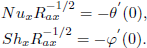(18)

III. RESULTS AND DISCUSSION

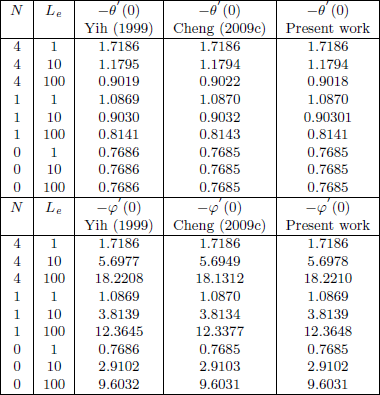
The system of coupled ordinary differential Eqs. (14)- (16) with the boundary conditions (17) are solved numerically using fourth order Runge-Kutta method along with the shooting technique. In order to verify the accuracy of the present method, the results have been compared with those of Yih (1999) and Cheng (2009c). The comparisons are found to be in good agreement as shown in Table 1.

Table 1. Comparison of values of -θ´(0) and -φ(0) for various values of N and Le with n = 1 , α = 0, D_f = 0, Sr = 0, λ = 0, δ = 0 and γ = 0.

The effects of the viscosity parameter α and the thermal radiation parameter R on the local Nusselt number 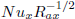and the local Sherwood number 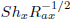are displayed in Figs. 2 and 3 for both cases n < 1 and n > 1.

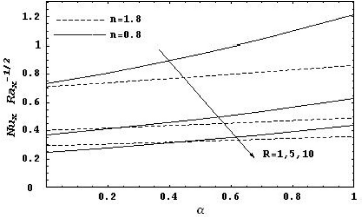
Figure 2: Local Nusselt number as a function of α for various values of R with N = 1, L_e = 1, D_f = 0.5, Sr = 0.5, γ = 0, γ^* = 0, δ = 0 and λ = 0.5

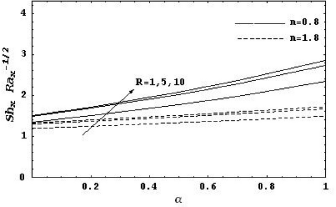
Figure 3: Local Sherwood number as a function of α for various values of R with N = 1, L_e = 1, D_f = 0.5, Sr = 0.5, γ = 0, γ^* = 0, δ = 0 and λ = 0.5

It is observed from Figs. 2 and 3 that as α increases, the local Nusselt number and the local Sherwood number increase.

It is also shown that increasing R leads to increase the local Nusselt number and the local Sherwood number for both cases n < 1 and n > 1. Figures 4 and 5 show the effect of the buoyancy parameter N and the power index of the wall temperature and concentration λ on the local Nusselt number and the local Sherwood number. It can be seen that the local Nusselt number or the local Sherwood number increase as N or λ increase.

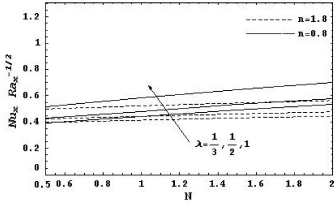
Figure 4: Local Nusselt number as a function of N for various values of λ with R = 5, L_e = 1, D_f = 0.5, Sr = 0.5, γ = 0, γ^* = 0, δ = 0 and α = 0.5

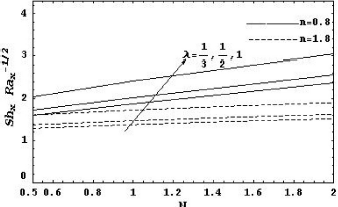
Figure 5: Local Sherwood number as a function of N for various values of λ with R = 5, L_e = 1, D_f = 0.5, Sr = 0.5, γ = 0, γ^* = 0, δ = 0 and α = 0.5

Figures 6 and 7 show the effects of Soret parameter S_r and Dufour parameter D_f on the local Nusselt number and the local Sherwood number for both pseudoplastics and dilatant fluids.From these figures it is noted that increasing the Dufour parameter l_e to decrease the local Nusselt number and to increase the local Sherwood number. Soret parameter has the opposite effect.

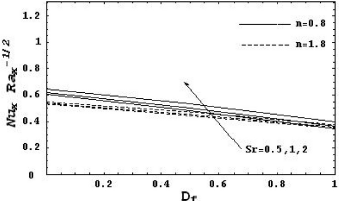
Figure 6: Local Nusselt number as a function of Df for various values of Sr with R = 5, L_e = 1, N = 1, λ = 0.5, γ = 0, γ^* = 0, δ = 0 and α = 0.5

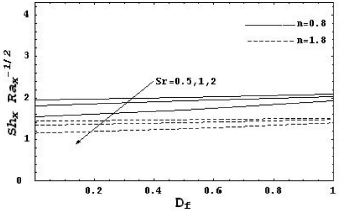
Figure 7: Local Sherwood number as a function of D_f for various values of Sr with R = 5, L_e = 1, N = 1, λ = 0.5, γ = 0, γ^* = 0, δ = 0 and α = 0.5

The effects of the heat generation parameter and the chemical reaction parameter on the local Nusselt number and the local Sherwood number are displayed in Figs. 8 and 9, respectively.It is shown that the chemical reaction parameter has the effect of depressing the local Nusselt number and enhancing the local Sherwood number, while the opposite is true for the effect of heat generation parameter.

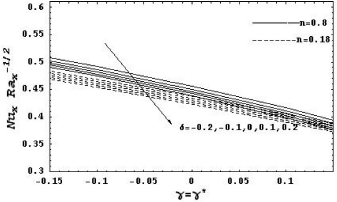
Figure 8: Local Nusselt number as a function of γ for various values of δ with R = 5, L_e = 1, N = 1, λ = 0.5, D_f = 0.5, Sr = 0.5 and α = 0.5

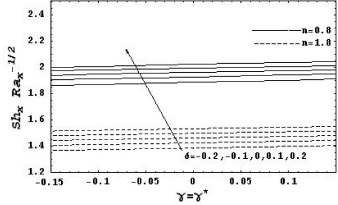
Figure 9: Local Sherwood number as a function of γ for various values of δ with R = 5, L_e = 1, N = 1, λ = 0.5, D_f = 0.5, Sr = 0.5 and α = 0.5

IV. CONCLUSIONS

The present work examined the effects of thermal radiation, variable viscosity and non uniform heat generation/ absorption on free convection boundary layer heat and mass transfer adjacent to a non-isothermal vertical full cone immersed in a porous medium with a non-Newtonian power-law fluid in the presence of Soret, Dufour and chemical reaction. The governing equations describing the problem are transformed to a system of coupled nonlinear ordinary differential equations using similarity transformation, where numerical solution has been presented for various values of the parameters. The numerical results indicated that the local Nusselt number and the local Sherwood number tend to increase as the viscosity parameter increases. It was found that increasing the thermal radiation parameter leads to decrease the local Nusselt number and an increase in the local Sherwood number. Also, it was noted that the local Nusselt number and the local Sherwood number increase as the power index of the wall temperature and concentration or the buoyancy ratio increases. However, it was displayed that the Soret parameter has the effect of enhancing the local Nusselt number and depressing the local Sherwood number. The Dufour parameter has an opposite effect. Moreover, it was illustrated that increasing the chemical reaction parameter or the heat generation parameter leads to decreasing the local Nusselt number and increasing the local Sherwood number.

REFERENCES
1. Alam, M.S. and M.M. Rahman, "Dufour and Soret effects on mixed convection flow past a vertical porous flat plate with variable suction," Nonlinear Analysis: Modelling and Contral , 11, 3-12 (2006).
2. Bagai, S., "Effect of variable viscosity on free convection over a non-isothermal axisymmetric body in a porous medium with internal heat generation," Acta Mechanica , 169, 187-194 (2004).
3. Bêg, O.A., A.Y. Bakier and V.R. Prasad, "Buoyancy driven Magneto convective Heat and Mass Transfer Past a stretching surface in fluid saturated Darcy porous medium with Soret/Dufour effects," Computational Material Science , 46, 57-65 (2009).
4. Cheng, P., T.T. Le and I. Pop, "Natural convection of a Darcian fluid about a cone," Int. Commun. Heat Mass Transfer , 12, 705-717 (1985).
5. Cheng, C.Y., "Nonsimilar boundary layer analysis of double-diffusive convection from a vertical truncated cone in a porous medium with variable viscosity," Applied Math. Comput. , 212, 185-193 (2009a).
6. Cheng, C.Y., "Natural convection heat transfer of non-Newtonian fluids in porous media from a vertical cone under mixed thermal boundary conditions," Int. Comm. Heat Mass Transfer , 36, 693-697 (2009b).
7. Cheng, C.Y., "Soret and Dufour effects on natural convection heat and mass transfer from a vertical cone in a porous medium," Int. Comm. Heat Mass Transfer , 36, 1020-1024 (2009c).
8. Cheng, C.Y., "Soret and Dufour effects on natural convection boundary layer flow over a vertical cone in a porous medium with constant wall heat and mass fluxes," Int. Comm. Heat Mass Transfer , 38, 4448 (2011).
9. Groşan, T., A. Postelincu and I. Pop, "Free convection boundary layer over a vertical cone in a non-Newtonian fluid saturated porous medium with internal heat generation," Technische Mechanik, Band , 24, 91-104 (2004).
10. Kumari, M. and S. Jayanathi, " Uniform lateral mass flux on natural convection flow over a vertical cone embedded in a porous medium saturated with a non-Newtonian fluid," J. Porous Media , 8, 73-84 (2005).
11. Lai, F.C. and F.A. Kulacki, "Coupled heat and mass transfer by natural convection from vertical sur-faces in porous media," Int. J. Heat Mass Transfer , 34, 1189-1191 (1991).
12. Mehta, K.N. and K.N. Rao, "Buoyancy induced flow of non-Newtonian fluids in a porous medium past a vertical flat plate with non uniform surface heat flux," Int. J. Engng. Sci., 32, 297-302 (1994).
13. Raptis, A., "Radiation and viscoelastic flow," Int. Comm. Heat Mass Transfer , 26, 889-895 (1999).
14. Reddy, M.G. and N.B. Reddy, "Soret and Dufour effects on steady MHD free convection flow past a semi-infinite moving vertical plate in a porous medium with viscous dissipation," Int. J. of Appl. Math. and Mech., 6, 1-12 (2010).
15. Tai, B.C. and M.I. Char, "Soret and Dufour effects on free convection flow of non-Newtonian fluids along a vertical plate embedded in a porous medium with thermal radiation," Int. Comm. Heat Mass Transfer, 37, 480-483 (2010).
16. Yih., K.A., "Uniform lateral mass flux effect on natural convection of non-Newtonian fluids over a cone in porous media," Int. Comm. Heat Mass Transfer, 25, 959-968 (1998).
17. Yih, K.A., "Coupled heat and mass transfer by free convection over a truncated cone in porous media: VWT/VWC or VHF/VMF," Acta Mech., 137, 8397 (1999).

Received: November 28, 2011
Accepted: July 3, 2012
Recommended by Subject Editor: Walter