Análisis comparativo de los diferentes modelos de corrupción en subastas

Andrés Fioriti^*

^* Universidad Nacional del Sur, Departamento de Economía, e.mail:elpepi@gmail.com

enviado: Diciembre 2011
aceptado: Marzo 2012

Resumen
En la presente revisión se analizan los distintos trabajos que existen enmarcados en corrupción, tanto en subastas como en licitaciones. Se analizarán solamente los casos de corrupción en subastas unidimensionales. La división de los casos se hace según el pacto corrupto sea exógeno o endógeno.

Clasificación JEL: D01, D82

Palabras clave: Corrupción; Subastas; Licitaciones.

Abstract
This paper analyzes the different papers that are framed in corruption, not only in auctions but also in procurements. This survey only discusses corruption in one-dimensional auctions. The division of cases depends on the nature of the corrupt agreement, whether it is exogenous or endogenous.

JEL Classification: D01, D82.

Keywords: Corruption; Auctions; Procurements.

INTRODUCCION

En los últimos años ha habido un gran incremento de la cantidad de transacciones que se realizan mediante el mecanismo de subastas, lo cual generó que la modelización teórica sobre el comportamiento de los agentes se convierta en un área de gran importancia para el análisis económico.

Un hecho sustancial de la realización de subastas es que son organizadas por agentes distintos a los dueños de los objetos (para el caso de las licitaciones los que la organizan son distintos a los que compran los objetos), por lo cual el organizador tiene incentivos a no ser neutral en su comportamiento y a tratar de maximizar su propio beneficio.

Este hecho es el que motiva estudiar cómo afecta la corrupción a los resultados de una subasta y qué medidas se pueden tomar para conseguir mecanismos competitivos que permitan la transparencia y el descubrimiento de precios, siendo este último punto de particular interés dado que cuando no se conoce el valor de un bien se considera que la mejor aproximación es provista por una subasta (o una licitación).

Vale destacar que corrupción no significa colusión. Si bien pueden darse en forma conjunta, existen resultados que presentan soluciones a la corrupción incompatibles con las soluciones propuestas para la colusión, siendo un resultado típico que ante corrupción es mejor emplear subastas de segundo precio y ante colusión es mejor emplear subastas de primer precio.

Lo normal es suponer que la corrupción se da en el sector público, pero esto no es excluyente porque también puede darse en el sector privado si una empresa delega en sus empleados la compra o la venta de bienes mediante procedimientos de subasta o licitaciones.

Es importante a la hora de comprender por qué se genera la corrupción tener en cuenta que la vulnerabilidad depende del tipo de bien o servicio que se pretende vender o adquirir y las distintas etapas del proceso donde puede aparecer corrupción.

A grandes rasgos existen cuatros tipos diferentes de bienes en el caso de licitaciones:

1. Proyectos que involucran un proceso de investigación y/o desarrollo especializado. Ej. Equipamiento militar.
2. Proyectos complejos con un propósito especial. Ej. Diques o instalaciones portuarias.
3. Productos habitualmente disponibles en mercados desarrollados, pero para los que se requiere una adaptación particular. Ej. Móviles policiales, ambulancias o sistemas informáticos.
4. Productos estandarizados de producción y consumo habituales. Ej. Papelería o insumos médicos.

Las instancias en las cuales se divide el proceso de contratación y las principales preguntas para cada caso son las siguientes:

• Antes de la recepción de las ofertas

1. ¿Es la contratación necesaria o no?
2. ¿Qué es exactamente lo que se va a comprar o contratar?
3. ¿Cuáles son las condiciones y especificaciones técnicas y financieras?
4. ¿Puede reducirse la entrada de competidores? Esta pregunta es de vital importancia porque la cantidad de competidores es una variable crucial para el éxito de cualquier licitación.

• Durante el procedimiento de recepción de ofertas y determinación del ganador.

1. ¿Cuál es el formato de la subasta empleada? Es decir ¿cómo se emiten las ofertas y cómo se las compara?

• Luego de la determinación del ganador.

1. ¿Cómo se controlará el cumplimiento de las condiciones del contrato?
2. ¿Habrá lugar para renegociaciones?

Las prácticas corruptas se pueden dar en cualquiera de las etapas y con cualquier tipo de bien. Si bien los bienes estandarizados tienen menos margen de discrecionalidad, se pueden modificar los plazos o la cantidad a adquirir, o se les puede introducir modificaciones para que pasen de ser un bien estandarizado a un bien que necesite una adaptación específica.

Además en todos los países existen regulaciones más estrictas en compras de grandes montos, por lo cual existe la opción de realizar muchas compras menores y dar lugar a corrupción.

Con lo dicho hasta el momento queda claro que las prácticas corruptas se pueden dar en una gran cantidad de situaciones, por lo cual se debe recurrir a distintos modelos que analicen diferentes aspectos para tratar de comprender en su totalidad el fenómeno.

La literatura existente a nivel teórico es aún pequeña y se enmarca dentro de la "teoría de subastas" (más en general en el área de "diseño de mecanismos").

Prácticamente todos los trabajos se orientan a la vulnerabilidad a la corrupción durante la etapa de recepción de ofertas y la determinación del ganador, que constituye la segunda etapa en la introducción planteada.

La literatura puede ser dividida en dos grandes ramas dentro de la teoría de subastas:

• Subastas unidimensionales: El precio es la única variable en la que se compite.
• Licitaciones multidimensionales: Se compite en precio y calidad. (Estos casos no serán tratados en el presente trabajo)

En todos los modelos se realiza la compra de un bien indivisible y de tamaño prefijado y se genera un acuerdo corrupto entre el subastador y al menos uno de los participantes.

Para finalizar esta sección es importante mencionar que se utilizará la definición de Lengwiler y Wolfstetter sobre los tipos de corrupción que existen en subastas unidimensionales:

• Tipo I: Se permite que un agente disminuya su oferta y aún así ganar la subasta.
• Tipo II: Se permite que un agente aumente su oferta y así poder ganar la subasta.

II. SUBASTAS UNIDIMENSIONALES

El modelo básico sin corrupción supone que existen 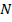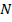agentes, cuyas valuaciones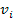 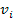están distribuidas según la función de distribución acumulada F en el intervalo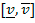 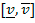con una función de densidad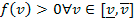 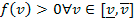. Los modelos trabajan con valuaciones privadas e independientes, por lo cual cada oferente conoce su propia valuación y la función de distribución de la cual surgen las valuaciones de los restantes participantes pero no la valuación en sí. Este conjunto de supuestos representa las condiciones normales que se utilizan en la modelización de subastas y se denotarán "supuestos estrella".

Lo que buscan los modelos son las estrategias 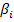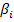de equilibrio, y se concentran en equilibrios simétricos porque dado que todos los participantes de la subasta tienen la misma información entonces el equilibrio debería ser igual para todos. Las estrategias tienen la función de mapear las valuaciones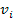 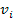a la ofertas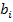 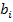, por ende .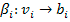

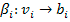Para una subasta de segundo precio en sobre cerrado (SSP) la estrategia débilmente dominante es 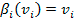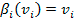, por lo cual la estrategia de cada agente es ofrecer su valuación.

Para una subasta de primer precio en sobre cerrado (SPP) la estrategia de equilibrio es:

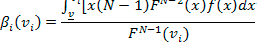En pos de analizar la eficiencia de la subasta (que en teoría de subastas se relaciona con que la subasta sea ganada por el oferente con mayor valuación) se puede decir que si 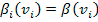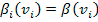, en otras palabras que el equilibrio es simétrico, y que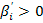 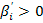, o sea que a mayor valuación mayor oferta, entonces la subasta es eficiente.

Un resultado muy importante de la teoría de subastas es el principio de equivalencia del ingreso que precisa que se cumplan cuatro condiciones:

1. Los jugadores son neutrales al riesgo
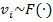
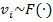2. con 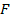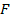continua, creciente e independiente (las valuaciones son i.i.d.).
3. Las reglas de la subasta son tales que le otorgan utilidad nula a un oferente con .
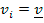
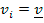4. Se cumple que la subasta es eficiente.

Si se dan estas condiciones entonces el ingreso del vendedor y la utilidad esperada de los compradores son independientes de las reglas de la subasta y por ende iguales entre subastas del mismo tipo. Por ejemplo en la SPP y la SSP estas condiciones se cumplen, cuando no hay corrupción, y entonces gana el mismo oferente y paga lo mismo independientemente del mecanismo.

III. SUBASTAS UNIDIMENSIONALES CON CORRUPCION

Dentro de esta rama de la literatura, la más explorada dentro de la corrupción en subastas, se encuentran distintos trabajos que se presentarán sucintamente y luego serán desarrollados con más detalle:

Arozamena y Weinschelbaum (2009) consideran que el acuerdo de favorecer a un agente se toma antes de que se realice la subasta y es exógeno, y extienden el análisis de Burguet y Perry (2007) al caso de 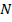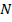agentes, caracterizando el comportamiento de los agentes cuando hay corrupción y cómo se modifican los resultados de la subasta. En este trabajo no prestan atención a cómo se dividen las ganancias de la corrupción.

Burguet y Perry (2007) se centran en el caso de dos oferentes y uno de ellos va a ser favorecido, lo cual se determina en forma exógena y antes de que tenga lugar la subasta. El agente favorecido puede elevar su oferta para ganar la subasta en los casos en los cuales perdería de no tener esta opción. El trabajo se concentra en los efectos que tiene la división de las ganancias derivadas de la corrupción entre el agente favorecido y el subastador y no tanto en cómo la corrupción afecta los resultados de la subasta.

Compte et. al. (2005) consideran la situación en la cual el subastador hace pública la oferta ganadora y permite que todos los oferentes compitan en sobornos por la chance de re ofertar. El paper hacer hincapié en la competencia en sobornos y sus efectos.

Koc y Neilson (2008) analizan el caso de corrupción antes de realizar las ofertas pero luego de que los agentes conocen sus valuaciones, y plantean la posibilidad de comprar el derecho a participar en una subasta de segundo precio a cambio de un soborno fijo.

Menezes y Monteiro (2006) plantean una situación en la cual el subastador le ofrece al agente que realizó la oferta más alta la opción de disminuir su oferta, manteniéndolo como ganador de la subasta, a cambio de un soborno.

Lengwiler y Wolfstetter (2010) analizan el caso en el cual el subastador le puede ofrecer al agente que realizó la mayor oferta disminuirla y aún así ganar u ofrecerle al agente que realizó la segunda mayor ofertar aumentarla y así ganar la subasta, exigiendo un soborno en ambos casos.

Estos trabajos pueden ser divididos entre aquellos en los cuales el pacto corrupto se da en forma exógena, se establece antes de la subasta, o aquellos trabajos en los cuales el oferente favorecido surge en forma endógena. Dentro de los primeros se encuentran Arozamena y Weinschelbaum (2009) y Burguet y Perry (2007). En la segunda rama están Compte et. al. (2005), Koc y Neilson (2008), Menezes y Monteiro (2006) y Lengwiler y Wolfstetter (2010).

III. 1. Pacto corrupto exógeno

Los dos modelos que componen esta rama de la literatura son modelos que asumen la existencia de corrupción entre el subastador y un agente y analizan cómo se ve afectada la subasta con esta modificación respecto del modelo sin corrupción.

Son modelos que sirven para explicar relaciones de largo plazo entre el subastador y un oferente, más allá de la subasta en curso. Entonces el subastador solo se relaciona con ese oferente en particular para evitar penalizaciones potenciales en subastas futuras.

III. 1. 1. Arozamena y Weinschelbaum (2009)

Modelo

Al igual que la mayoría de los trabajos que se van a comentar en la presente revisión de la literatura, los autores se concentran en la subasta de primer precio, dado que para el caso de una subasta de segundo precio sigue siendo una estrategia débilmente dominante, pese a agregar la posibilidad de corrupción, ofrecer la propia valuación.

Su modelo se basa en todos los supuestos estrella.

A los supuestos estrella los autores agregan el supuesto de que 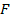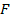es log cóncava (esta condición se cumple para la mayoría de las funciones de distribución), y por ende definen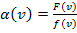 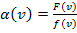. Además definen a la inversa de la estrategia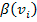 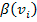como 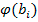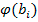, donde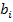 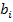es la oferta que realiza un agente cuya valuación es .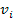

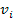Al momento de agregarle corrupción al modelo los autores suponen que la relación entre el subastador y el oferente deshonesto es de largo plazo y exógena a los parámetros del modelo. Además no especifican cómo se dividen las ganancias derivadas de la corrupción.

Si 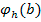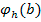representa la función inversa de oferta de los oferentes honestos, entonces los honestos tienen como función objetivo:

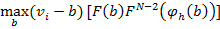Aquí 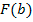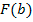se refiere al oferente deshonesto y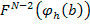 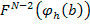hace referencia a los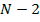 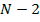rivales honestos del honesto en cuestión.

La ecuación diferencial del presente modelo, dado un equilibrio simétrico, queda caracterizada por la función:

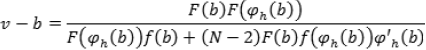Comportamiento

En este modelo la oferta inicial del agente deshonesto no tiene significado porque una vez que se realizan las ofertas el subastador le informa cuánto ofertaron todos los participantes y le permite revisar su oferta, tanto hacia arriba como hacia abajo (se permite corrupción tipo I y tipo II).

Siendo la oferta del agente deshonesto 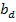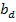y 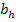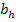la oferta más alta realizada en primera instancia por uno de los honestos, entonces:

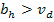
• Si 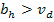el agente deshonesto pierde la subasta, porque se debe cumplir que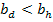 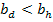(sino ganaría la subasta pero obtendría un pago negativo, lo cual no es racional).
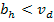
• Si 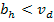entonces el agente deshonesto va a ofrecer, en segunda instancia,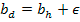 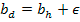y ganará la subasta.

Teniendo presente este comportamiento del deshonesto es posible comprender por qué los agentes honestos compiten contra las ofertas de los otros 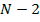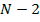honestos y contra la valuación del deshonesto.

Los resultados más relevantes del modelo en cuanto a las modificaciones en el comportamiento de los honestos se expresan en función de y se resumen en el siguiente cuadro:

Cuadro I

Fuente: Arozamena y Weinschelbaum (2009).

Donde 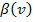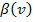es la función de oferta de los honestos cuando no hay corrupción y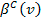 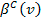es la función de oferta de los honestos cuando hay corrupción.

Eficiencia

Es importante precisar que en una subasta de primer precio hay lugar a ineficiencias. En este tipo de subastas el óptimo es ofrecer un valor menor a la valuación porque de ofrecer un monto igual a la valuación y ganar la subasta el beneficio obtenido sería nulo, por ende 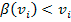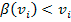, y entonces si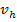 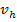es la valuación del agente que más valúa el bien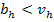 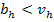y la ineficiencia se observa en la siguiente figura:

Figura I

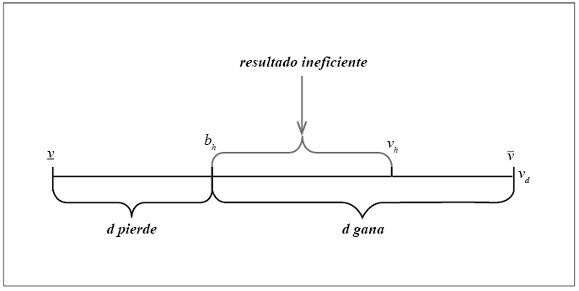
Fuente: Arozamena y Weinschelbaum (2009)

Como se puede observar existen lugares en los cuales el oferente honesto valúa más el bien que el deshonesto pero aún así pierde la subasta como consecuencia de la diferencia que existe entre su valuación y su oferta.

Bienestar

Para analizar el impacto de la corrupción en el bienestar los autores mencionan dos efectos:

• Efecto directo: Es el efecto sobre la utilidad esperada de todos los agentes como resultado de la corrupción. Se fija la estrategia de los honestos y cuando se le añade corrupción entonces pierden en algunos casos en los que antes hubiesen ganado, por lo cual su utilidad disminuye.
• Efecto percepción: Es el cambio en la utilidad esperada de cualquier agente como consecuencia exclusiva de que los agentes honestos modifican su comportamiento ante la presencia de un agente deshonesto.

Para los oferentes honestos el efecto directo es siempre negativo (recordar que pierden en algunos casos donde antes ganaban la subasta) y el efecto percepción depende de :

• Es positivo si es estrictamente cóncavo.
• Es negativo si es estrictamente convexo.
• Es cero si es lineal.

El efecto total sobre su utilidad es negativo si es lineal o estrictamente convexo, mientras que si es estrictamente cóncavo dependerá de la relación entre las magnitudes del efecto directo y el efecto percepción.

Para los dos agentes corruptos (el subastador y el oferente deshonesto) no existe efecto directo sobre su utilidad y el efecto percepción:

• Es positivo si es estrictamente cóncavo.
• Es negativo si es estrictamente convexo.
• Es cero si es lineal.

El oferente deshonesto está mejor con corrupción si es lineal o estrictamente convexo.

Pago esperado

Los autores llegan a la conclusión de que, bajo casos regulares (recurriendo a funciones de distribución comúnmente utilizadas), la utilidad esperada del vendedor siempre disminuye bajo corrupción en relación al caso libre de corrupción. En otras palabras, cae el pago esperado. Este resultado era esperable dado que es un resultado conocido que la subasta óptima de primer precio para el vendedor es aquella libre de corrupción, por lo cual cualquier otro mecanismo le generará ingresos iguales o menores. Sin embargo agregan en su trabajo un caso no regular en el cual el ingreso esperado para el vendedor aumenta bajo la presencia de corrupción, dado que los honestos sobre-reaccionan.

Un resultado de gran relevancia es que la existencia de corrupción, en un contexto de costo de entrada a la subasta positivo, hace que menos agentes participen de la subasta de los que deberían (participan menos oferentes que el 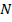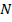óptimo) y esto hace que disminuya la competencia, implicando que los agentes ofrezcan menos agresivamente y disminuyendo aún más el ingreso del vendedor, a la vez que aumenta el excedente del cual se apropian el subastador y el oferente deshonesto.

III. 1. 2. Burguet y Perry (2007)

Modelo

Este trabajo es sobre una licitación, aunque aquí será tratado como una subasta dado que las conclusiones son análogas y simplemente hay que realizar ciertas modificaciones en su notación, sin pérdida alguna de contenido.

A diferencia del modelo precedente, en este caso los autores analizan el caso de 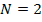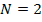. Ahora habrá un agente deshonesto (igual que en el modelo anterior) y un solo agente honesto, siendo un rasgo distintivo de este modelo que sus valuaciones pueden surgir de distribuciones distintas -surgirán de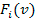 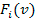con 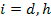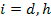-. Por último los autores acotan las valuaciones al intervalo .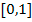

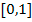Las diferencias con los supuestos estrella son que ahora 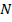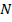no puede tomar cualquier valor si no que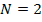 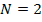y las funciones de distribución de las valuaciones ya no son necesariamente las mismas para todos los oferentes.

Nuevamente el acuerdo corrupto tiene lugar antes de la subasta, dado que suponen una relación de largo plazo, y entonces cada agente sabe si es el honesto o el deshonesto.

Comportamiento

La principal diferencia con el modelo de Arozamena y Weinschelbaum (2009) es que aquí solo puede tener lugar corrupción del tipo II: el deshonesto solo puede subir su oferta si no ganó, pero no la puede bajar. Los casos posibles que se pueden dar son los siguientes (recordar que como 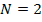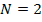hay un solo honesto, por ende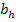 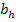es la única oferta que hay de los honestos):

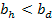
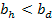1. , en este caso gana la subasta el deshonesto y paga lo que ofreció.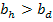
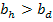2. y 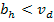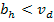, en este caso opera la corrupción y existe un excedente de la corrupción de magnitud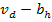 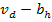del cual los participantes del acuerdo corrupto pueden apropiarse.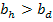
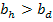3. y 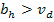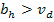, en este caso no hay lugar para la corrupción y el agente honesto gana la subasta, pagando lo que ofreció (no opera la corrupción porque para ganar la subasta el agente deshonesto debería ofrecer por encima de su valuación y obtendría utilidad negativa, lo cual no es racional).

En el caso en el cual puede haber corrupción la opción para el deshonesto es igualar la oferta del honesto (o lo que es lo mismo, para comparar con el modelo anterior, ofrecer 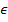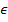más) y así ganar la subasta, y el excedente generado se dividirá en una proporción para el subastador y la proporción restante, 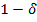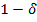, para el deshonesto.

Al ser solo dos agentes, como el honesto está obligado a ofrecer por encima de la valuación del deshonesto si quiere ganar la subasta, entonces su estrategia será ofrecer por encima de 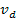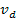siempre y cuando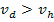 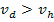y si no perder la subasta.

Formalmente el honesto busca maximizar:

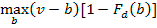La condición de primer orden para el honesto es:

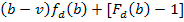Para el caso del deshonesto su función objetivo es de la forma:

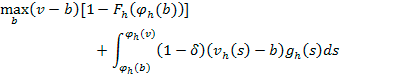Implícitamente la estrategia del deshonesto queda definida mediante la condición de primer orden:

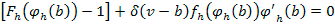Donde 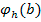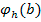es la función inversa de oferta del honesto.

Dado que su análisis se centra en estudiar cómo afecta la distribución del excedente derivado de la corrupción (que puede ser entendido como el soborno), el parámetro de su interés es . De la estrategia del deshonesto, y teniendo en cuenta que al honesto no le afecta porque solo debe ganarle a la valuación del deshonesto independientemente de lo que haga él, se observa que a mayor mayor es 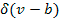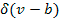, y dado que debe igualarse a cero la condición de primer orden entonces mayor tendrá que ser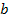 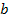, dado que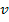 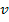viene dado y no es una variable que pueda modificar el agente. En otras palabras, cuanto más excedente se apropie el licitador entonces más agresivo será el agente deshonesto.

Pago esperado

El primer análisis que hacen Burguet y Perry es cómo se modifica el pago esperado cuando varía . Como consecuencia lógica de que 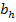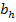no depende de y 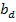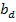crece a medida que crece , y como el precio esperado por el vendedor es 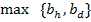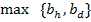, entonces el precio esperado es creciente en , lo cual representa un resultado no trivial porque a mayor significa que el subastador se apropia de mayor parte del excedente, y mediante esta vía mejora el ingreso del vendedor.

El otro análisis que realizan en este rubro es sobre los efectos que tiene la corrupción sobre el ingreso esperado comparándola con el caso sin corrupción y con la subasta de segundo precio, y concluyen el mismo resultado que Arozamena y Weinschelbaum (2009) sobre la falta de certeza en las comparaciones, dado que encuentran casos donde la corrupción eleva el pago esperado y casos en los cuales este cae, concluyendo que la corrupción tiene efectos ambiguos.

Eficiencia

El análisis que realizan, donde permiten asimetría en la distribución de las valuaciones entre los agentes, ocasiona que los efectos de la corrupción sobre la eficiencia sean ambiguos.

Partiendo de distribuciones asimétricas la asignación, sin corrupción, es ineficiente porque le otorga el bien al oferente débil en caso en los cuales su valuación es inferior. Al agregar corrupción el agente deshonesto gana en mayor cantidad de casos que en la situación inicial. Si el deshonesto es el agente fuerte se corrige la ineficiencia que existía sin corrupción, mientras que si es el agente débil entonces la ineficiencia se potencia.

Bienestar

Los autores no analizan el impacto del efecto directo ni del efecto percepción, sino que simplemente se limitan al efecto agregado y concluyen que el honesto pierde utilidad bajo la presencia de corrupción y, si bien no lo prueban, mencionan que la corrupción es beneficiosa tanto para el deshonesto como para el subastador dado que existe un beneficio que ellos se reparten, que de no existir la corrupción no se podrían distribuir.

III. 2. Conclusiones sobre pacto de corrupción exógeno

Los casos examinados son los de corrupción tipo I y tipo II, en forma conjunta, en Arozamena y Weinschelbaum (2009) (AW) y corrupción tipo II en Burguet y Perry (2007) (BP), no teniendo en cuenta qué pasa si solo se permite corrupción tipo I o qué pasa si son mutuamente excluyentes (tal como se mostrará más adelante que lo analizan Lengwiler y Wolfstetter (2010)).

El resultado más importante es la incertidumbre sobre la reacción de los honestos al pasar de competir contra la oferta de todos los agentes a competir contra la valuación del agente deshonesto dado que saben que éste podrá modificar su oferta y la oferta de los honestos restantes. Tanto en AW como en BP este efecto es evidente y es el que le da gran importancia al análisis de los efectos de la corrupción, dado que es un resultado no trivial.

En el caso en el cual los valuaciones surgen de la misma distribución el impacto de la corrupción sobre la eficiencia es negativo (AW), mientras que el impacto sobre la eficiencia en el caso de BP, en el cual las valuaciones surgen de distintas distribuciones (los agentes son asimétricos), es indeterminado (depende de que el deshonesto sea el competidor fuerte o el débil).

En cuanto a la caracterización del precio esperado que recibe el vendedor comparando los casos con y sin corrupción AW encuentran que la corrupción hace que tal precio caiga (siempre y cuando las valuaciones surjan de distribuciones regulares), mientras que el efecto en BP es indeterminado producto de la asimetría de los agentes.

Para los oferentes honestos la corrupción siempre impacta negativamente en su bienestar, dado que ahora enfrentan una competencia más agresiva (pasan de competir contra la oferta del otro oferente a competir contra su valuación, la cual es siempre superior a su oferta en una subasta de primer precio).

Por último, pero aún así no menos importante, AW y BP permiten sospechar que tanto el subastador como el agente deshonesto se benefician de la corrupción, por lo cual sería difícil de combatir la corrupción mediante mecanismos que le den incentivos para que no utilicen prácticas corruptas.

Una crítica que se le hace a este tipo de modelos es que no explican cómo surge la corrupción, sino que parten de su existencia y se fijan si se justifica o no en términos económicos. La conclusión que encuentran es que existe un excedente del cual se apropian los que participan en la práctica corrupta, por lo cual logran demostrar que la corrupción en sí tiene razón de ser.

III. 3. Pacto corrupto endógeno

En este tipo de modelos el acuerdo entre el subastador y los oferentes (ya sea uno o varios de ellos) surge como consecuencia misma del proceso de la subasta. Su utilidad es importante para analizar vínculos esporádicos entre subastador y oferentes, de los cuales cada uno extrae un beneficio y después se volverán a relacionar en caso que los dos se beneficien o de lo contrario no lo harán, y no existe la opción de recibir penalizaciones en el futuro por la contraparte del contrato.

Los trabajos en esta rama se pueden dividir en dos categorías, perteneciendo dos trabajos a cada categoría:

1. Modelos donde los oferentes compiten en forma simultánea en ofertas y en sobornos. Es el caso de Compte et. al. (2005) y Koc y Neilson (2008). Estos modelos tienen como crítica que el subastador involucra a un gran número de oferentes en el pacto corrupto y por ende no parecen muy viables en la práctica.
2. Modelos donde luego de recibidas las ofertas se genera un acuerdo corrupto sin competencia en sobornos. Es el caso de Menezes y Monteiro (2006) y Lengwiler y Wolfstetter (2010). En este caso los implicados en el acuerdo corrupto son el subastador y el agente que recibe la oferta para pagar un soborno.

III. 3. 1. Compte, Lambert-Mogiliansky y Verdier (2005)

Modelo

Agregan a los supuestos estrella un precio de reserva mínimo igual a 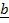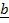. Ordenan las valuaciones de mayor a menor, siendo esto una modificación menor en el análisis con respecto a los supuestos estrella, por lo cual .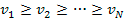

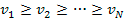En el caso en el cual no hay corrupción, pero hay un precio de reserva, y 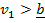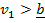, en cualquier equilibrio de la subasta el bien se adquiere a un precio como máximo igual a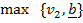 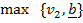(o se paga la segunda mayor valuación o el precio de reserva).

La subasta, en este caso, transcurre en tres etapas:

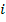
• Primera etapa: Cada oferente 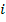realiza una oferta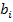 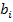, siendo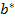 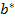la más alta.
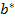
• Segunda etapa: El subastador revela 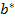y le permite a cada oferente ofrecerle un soborno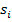 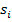, siendo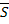 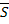el máximo soborno que puede recibir (dado que los autores suponen que de recibir un soborno superior entonces la corrupción sería detectada y no podría llevarse a cabo). El oferente que ofreció el soborno más alto puede modificar su oferta original, y si hay empate en el soborno más alto entonces se elige al azar cuál de ellos modificará su oferta y pagará el soborno.
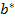
• Tercera etapa: Dadas las ofertas originales y la modificada, producto de la corrupción, el subastador anuncia qué oferta ganó la subasta (las únicas ofertas que pueden ganar son 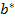o la oferta modificada).

Los autores postulan que 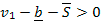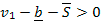si y si 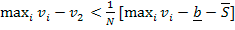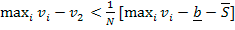, existe un equilibrio bayesiano perfecto en el que el contrato se asigna al precio de reserva .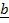

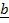Comportamiento

En este modelo desaparece la competencia entre los oferentes en cuanto a las ofertas. Ahora compiten en sobornos, pero como existe un máximo entonces en equilibrio todos ofrecerán el soborno máximo y ofrecerán el precio de reserva, ganando la subasta un oferente al azar que pagará el precio de reserva.

El modelo presenta un rasgo característico según el cual, al ofrecer todos el soborno máximo, no conviene desviarse de ofrecer el precio de reserva. Esto es así porque prácticamente con probabilidad uno algún oferente podrá revisar su oferta, entonces para evitar pagar el soborno un oferente debería ofrecer por encima de las valuaciones de todos los demás, pero el costo de ello es que debe ofrecer un monto sustancialmente mayor que el precio de reserva, y por ende no lo hace y opta por ofrecer el precio de reserva y pagar el soborno máximo. Esto es así porque ahora los oferentes maximizan su beneficio pagando el soborno y garantizándose pagar el precio de reserva y no sometiéndose a la subasta.

Los resultados obtenidos con respecto al comportamiento no dependen de la forma particular que revista el soborno, dado que también demuestran que si el soborno es un regalo al subastador, pero está acotado en cuál es el soborno máximo, entonces los resultados se mantienen.

Un resultado importante de los autores indica qué pasa cuando aparece un nuevo oferente que no tiene ningún tipo de conexión con el subastador y por ende no accede al mercado de sobornos. Al incentivar la competencia en ofertas, dado que este es el único rubro en el cual el agente ingresante puede competir, todos pasan a ofrecer más agresivamente, restaurando de esta forma la competencia en el mercado de ofertas y disminuyendo la competencia en sobornos, por lo cual concluyen que sería una buena medida de política permitir la participación de oferentes, sin nexos en el mercado en el cual se lleva a cabo la subasta, para dotar de competitividad a las subastas. O en otros términos se puede pensar que si al agregar un agente externo que no tiene posibilidad de sobornar los resultados cambian rotundamente, entonces el modelo no presenta demasiada robustez.

Eficiencia

Analizando la eficiencia se puede ver con gran claridad que en este tipo de modelos se pierde la eficiencia, dado que al ser elegido al azar quién va a ganar la subasta entonces no se puede garantizar que el elegido sea aquél que más valúa el bien.

En términos formales esto se puede observar en que la estrategia de equilibrio es ofrecer 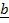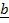y 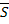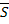, que son independientes de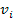 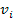, no garantizando que sean estrategias simétricas crecientes en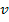 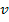. Por ende no es eficiente la subasta.

Pago esperado

Con respecto al pago esperado también es claro que disminuye. El vendedor, en el modelo sin corrupción, recibía una proporción de la máxima valuación, pero ese pago era como mínimo igual al precio de reserva y posiblemente mayor. En el presente modelo el pago esperado es igual al precio de reserva como consecuencia de la corrupción.

III. 3. 2. Koc y Neilson (2008)

Modelo

En este modelo se mantienen los supuestos estrella.

Al igual que en el modelo anterior la subasta transcurre en tres etapas.

• Primera etapa: El subastador elige un nivel de soborno ss fijo y le ofrece a todos los oferentes el siguiente mecanismo:

1. Si paga el soborno entonces el ganador la subasta no pagará lo que ofreció sino que pagará lo que ofreció el segundo que más ofreció.
2. Si no paga el soborno y gana la subasta entonces pagará lo que ofreció.

• Segunda etapa: Los oferentes deciden simultáneamente si pagan el soborno o no y también cuánto ofrecen en la subasta.
• Tercera etapa: Dadas las ofertas se determina el ganador. Si el ganador pagó el soborno entonces paga la segunda oferta más alta, si no pagó el soborno entonces paga lo que ofreció.

En este modelo no existe competencia en sobornos, sino que cada firma decide si paga o no el soborno y el hecho de pagarlo no excluye a otra firma de pagarlo también, por lo que la única competencia se da en ofertas.

Quienes pagan el soborno pasan a participar en un grupo mientras que los que no pagan el soborno forman parte de otro grupo. Si pertenece al grupo de los sobornadores participa de una subasta de segundo precio y su estrategia dominante pasa a ser .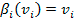

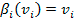Lo relevante del modelo es determinar quién paga el soborno y quién no.

Para determinarlo buscan caracterizar el punto de corte entre los grupos. La intuición es que si alguien con una valuación 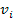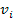no paga el soborno entonces tampoco lo pagará otro oferente con una valuación igual o menor, mientras que si alguien con una valuación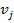 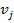paga el soborno entonces también lo pagará alguien con la misma o mayor valuación.

El punto de corte 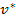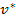queda caracterizado por:

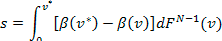En ese punto un oferente con valuación 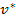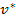se encuentra indiferente entre pagar el soborno o no. Todos aquellos con valuaciones superiores a él pagan el soborno y todos aquellos con valuaciones menores no lo pagan.

La justificación del punto de corte es que si un oferente con una valuación 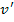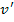paga el soborno entonces obtiene:

(1)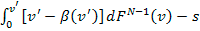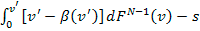

Si dicho oferente no paga el soborno entonces obtiene:

(2)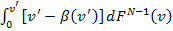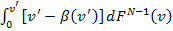

Para el oferente cuya valuación 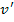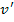es igual a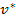 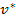(1) y (2) deben igualarse, por lo cual:

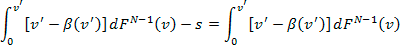Resolviendo esta igualdad se obtiene el punto de corte mencionado anteriormente.

Comportamiento

Todos aquellos que no pagan el soborno se comportan como si estuvieran frente a una subasta de primer precio, por lo cual mantienen la estrategia del modelo sin corrupción, mientras que todos los que pagan el soborno ofrecen su valuación y por ende se comportan como si estuvieran en una subasta de segunda precio.

En el gráfico a continuación se puede observar cómo funcionan las estrategias. Se asume que en la SPP la función de oferta es lineal y es una proporción de la valuación, mientras que en la SSP la función de oferta es ofrecer la valuación. Si bien en 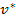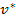existe un salto el gráfico deja en evidencia que la función de oferta es creciente en .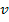

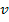Figura II

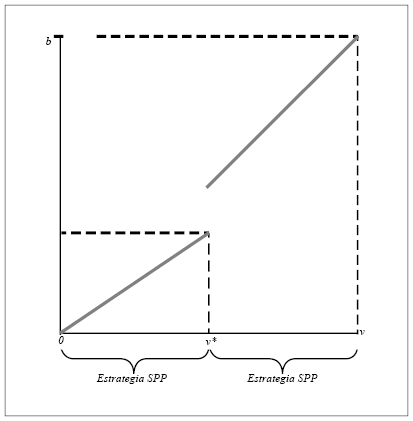
Fuente: Elaboración propia

Eficiencia

Dado que en esta subasta gana quien tiene la valuación más alta entonces la eficiencia no se ve afectada y por ende, pese a haber corrupción, la subasta es eficiente. Esto tiene lugar porque las estrategias de una SPP y una SSP son crecientes en 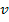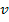y entonces el que más lo valúa al bien es el que más ofrece y gana la subasta.

Bienestar

Al aplicarse el teorema de equivalencia del ingreso entonces todos los oferentes obtienen la misma utilidad que en el caso sin corrupción, mientras que el subastador mejora su bienestar y el vendedor lo empeora dado que el soborno representa una transferencia del vendedor al subastador en relación al caso sin corrupción.

Pago esperado

El pago esperado por el vendedor es menor, dado que si nadie paga el soborno entonces el pago es el mismo pero si al menos uno ya paga el soborno (si es exactamente uno el que paga el soborno entonces va a ganar la subasta porque tiene la valuación más alta) entonces su pago esperado es menor y por ende, en el agregado, su pago esperado decae.

III. 3. 3. Menezes y Monteiro (2006)

Modelo

En este modelo se mantienen los supuestos estrella.

Al igual que en los dos modelos anteriores de corrupción endógena la subasta transcurre en tres etapas.

• Primera etapa: Los agentes realizan sus ofertas en forma simultánea.
• Segunda etapa: El subastador observa quién fue el que realizó la mejor oferta y le ofrece la opción de reducirla hasta la segunda mayor oferta, y aún así ganar la subasta, a cambio de un soborno proporcional.
• Tercera etapa: El subastador anuncia el ganador de la subasta, que será al que le ofreció el soborno independientemente de que lo haya pagado o no, y lo que debe pagar será la segunda mayor oferta si pagó el soborno y si no lo que ofreció.

Como característica diferencial con respecto a los modelos precedentes se destaca que sólo el subastador y el que realizó la mayor oferta están involucrados en el acuerdo corrupto, y siguiendo a los modelos de Koc y Neilson (2008) y Compte et. al. (2005) quién es el deshonesto es determinado endógenamente.

El soborno toma la forma de una proporción fija del excedente generado por la corrupción que es recibido por el subastador, mientras que al oferente corrupto le corresponde una proporción 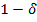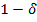de tal excedente.

Los autores también analizan el caso en el cual el soborno es una suma fija y llegan a las mismas conclusiones, por lo cual se destacarán solo los aspectos del modelo con soborno proporcional aunque los resultados son análogos.

Comportamiento

Dado que la corrupción es de conocimiento común entonces los agentes la anticipan y se llega a un equilibrio simétrico creciente de la forma:

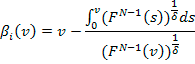A diferencia de Burguet y Perry (2007), en este modelo los oferentes su vuelven menos agresivos a medida que aumenta (la porción del excedente que se apropia el subastador). En el caso extremo en el cual 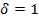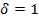la estrategia de los agentes es ofrecer igual que en una subasta de primer precio sin corrupción, lo cual es intuitivo dado que no se apropian de ningún excedente en caso de participar de la práctica corrupta y entonces los oferentes se comportan como si la corrupción no fuese una opción.

Otro rasgo importante de este modelo es que cuando 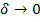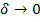entonces los agentes ofrecen acorde a lo que harían en una subasta de segundo precio. Este resultado también es intuitivo porque si se pueden apropiar de todo el excedente derivado de la corrupción entonces terminan ofreciendo como si lo que fueran a pagar es la segunda oferta más alta.

Eficiencia

La eficiencia no se ve modificada dado que se llega a un equilibrio simétrico creciente y entonces el oferente con la mayor valuación va a ser el que más va a ofrecer, y dado que gana independientemente de que pague o no el soborno entonces él (el oferente con la mayor valuación) será el que gane la subasta y el bien quedará en manos del que más lo valúa.

Bienestar y pago esperado

Al igual que en Koc y Neilson (2008) se aplica el teorema de equivalencia del ingreso entre la subasta de primer precio planteada y la de segundo precio, por lo cual el soborno representa una transferencia del vendedor al subastador.

Los oferentes obtienen la misma utilidad que en el caso sin corrupción. El único beneficiado por la práctica corrupta es el subastador, mientras que por el otro lado el único perjudicado es el vendedor, que termina recibiendo un pago menor al que hubiese recibido de no mediar corrupción.

Este trabajo hace alusión a la subasta de segundo precio pero en forma indirecta, dado que le agregan al modelo con corrupción aversión al riesgo, y como el riesgo no afecta a la SSP pero sí a la de primer precio (ocasionando que los oferentes sean más agresivos) analizan si la aversión "corrige" o no el pago esperado por el vendedor, concluyendo que pese a la aversión el pago esperado en una SPP con corrupción y aversión sigue siendo menor que aquél que obtiene en una SSP.

III. 3. 4. Lengwiler y Wolfstetter (2010)

Modelo

El modelo base es el mismo que Menezes y Monteiro (2006), aunque ahora el subastador tiene más libertad en la segunda etapa y la estructura del juego toma la siguiente forma:

• Primera etapa: Los agentes realizan sus ofertas en forma simultánea.
• Segunda etapa: El subastador analiza la diferencia que existe entre la mayor oferta y la segunda mayor oferta o entre la mayor oferta y la segunda mayor valuación, y le ofrece la opción de sobornar a aquel que tenga la mayor diferencia (dado que es mayor el excedente del cual se puede apropiar). Los dos casos posibles son los siguientes.

1. El subastador observa quién fue el que realizó la mejor oferta y le ofrece la opción de reducirla hasta la segunda mayor oferta, y aún así ganar la subasta, a cambio de un soborno. Este caso es de corrupción tipo I.
2. El subastador observa quién fue el que realizó la mejor oferta y quién realizó la segunda mayor oferta y le ofrece a este último la opción de aumentarla hasta igualar la mayor oferta, y así ganar la subasta, a cambio de un soborno. Este caso es de corrupción tipo II.

1. Tercera etapa: El subastador anuncia el ganador de la subasta. En caso de haber tenido lugar corrupción del tipo I será aquel al que le ofreció el soborno independientemente de que lo haya pagado o no, y lo que deberá pagar será la segunda mayor oferta si pagó el soborno y si no lo que ofreció. En caso de haber tenido lugar corrupción tipo II, ganará el que realizó la segunda mayor oferta en la primera etapa en caso de haber pagado el soborno y paga la mayor oferta de la primera etapa y si no gana el que pagó la mayor oferta en la primera etapa pagando lo que ofreció.

Al igual que en los modelos precedentes el soborno toma la forma de una proporción fija del excedente generado por la corrupción que es recibido por el subastador, mientras que al oferente corrupto le corresponde una proporción 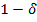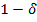de tal excedente. Esto depende de que el pacto corrupto se lleve a cabo, de lo contrario no hay excedente para repartir.

Comportamiento

Si bien el análisis de corrupción tipo I es análogo al realizado por Menezes y Monteiro (2006), el caso de corrupción tipo II es distinto. Para que opere este último tipo de corrupción el subastador tiene que saber cuál es la valuación del agente que realizó la segunda mayor oferta en la primera etapa, y esto es información privada, por lo cual debe operar algún mecanismo de señalización. Más formalmente el mecanismo que opera lo hace mediante la información que brinda la oferta realizada en la primera etapa.

Dado que este modelo no tiene solución analítica entonces solo se tendrán en cuenta sus conclusiones generales.

Eficiencia

Los autores encuentran un resultado que difiere del que encontraron los trabajos de Koc y Neilson (2008) y de Menezes y Monteiro (2006), dado que como ahora puede tener lugar corrupción tipo II entonces no siempre gana el que más valúa el bien, y ya no se garantiza eficiencia.

En la figura siguiente se puede observar dónde tiene lugar cada tipo de corrupción (tipo I y tipo II) y cuál es el área ineficiente (dónde gana un oferente cuya valuación no es la más alta).

Figura III

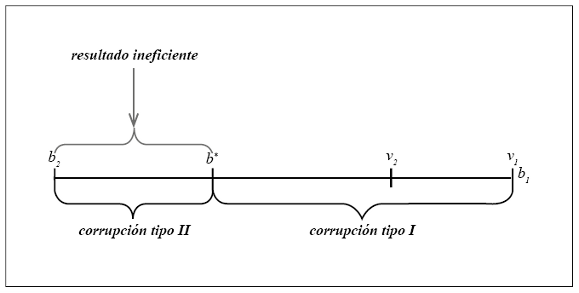
Fuente: Elaboración propia

En la figura 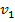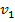y 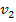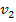representan la valuación más alta y la segunda valuación más alta, respectivamente, mientras que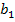 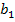y 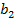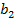representan la oferta del agente con la valuación más alta y la del agente con la segunda valuación más alta, respectivamente. Es importante notar que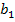 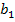nunca va a ser menor a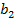 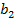si es que ambos jugadores utilizan la misma estrategia de oferta. El punto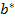 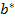representa la oferta en la cual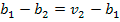 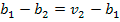, y es el punto en el cual el subastador está indiferente entre ofrecer el pacto corrupto al oferente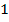 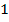o al oferente .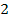

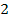El área marcada como ineficiente coincide con la corrupción tipo II, dado que allí gana el segundo que más valúa el bien.

Bienestar y pago esperado

Con respecto al bienestar y al pago esperado los autores demuestran, computacionalmente, que la corrupción representa una transferencia del vendedor hacia el subastador, por lo cual disminuye el bienestar del primero y aumenta el del último. Además el pago esperado cae, como en todos los modelos de corrupción endógena.

La utilidad de los oferentes no se modifica y por ende permanecen indiferentes entre el juego con corrupción y sin corrupción.

III. 4. Conclusiones sobre pacto de corrupción endógeno

En este apartado se presentarán en términos globales las conclusiones de los trabajos de Compte et. al. (2005) (CLV), Koc y Neilson (2008) (KN), Menezes y Monteiro (2006) (MM) y Lengwiler y Wolfstetter (2010) (LW).

Los trabajos de KN y MM se ajustan al principio de equivalencia del ingreso, dado que siguen una estrategia de equilibrio simétrica y creciente. Por ende gana el que tiene la mayor valuación y entonces se mantiene la eficiencia de la subasta.

Tanto en CLV como en LW la eficiencia se pierde. En el primero esto tiene lugar como consecuencia de que se elige al azar al ganador de la subasta entonces no necesariamente ganará aquél que más valúa el bien. En el segundo la eficiencia se pierde producto de permitirle al subastador ejercer corrupción tipo II.

En relación al precio esperado por el vendedor, cae en todos los modelos. En CLV recibe el precio de reserva, en KN recibe la segunda mayor oferta, mientras que en MM lo más probable es que reciba la segunda mayor oferta (dado que con probabilidad próxima a uno un oferente paga el soborno) y en LW no hay una solución específica acerca de cuánto recibe dado que en algunos casos puede recibir la mayor oferta y en otros la segunda mayor oferta.

Con respecto al impacto sobre el bienestar se expondrá a continuación una tabla a modo de resumen de los efectos enunciados en cada trabajo sobre la utilidad de cada tipo de agente (se hará la división entre honestos y deshonestos, aunque en los modelos de corrupción endógena la división no es tan clara dado que todos pueden ser deshonestos y por ende todos pueden ser honestos).

Tabla II

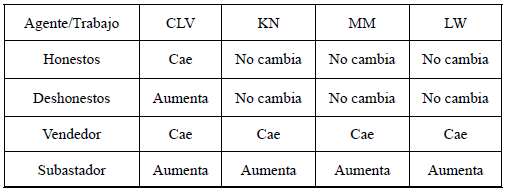
Fuente: Elaboración propia

REFERENCIAS BIBLIOGRAFICAS
1. Arozamena, L. y Weinschelbaum F., (2009), The Effect of Corruption on Bidding Behavior in First-Price Auctions, European Economic Review, Vol. 53, pp. 645-657.
2. Burguet, R. y Che Y., (2004), Competitive Procurement with Corruption, RAND Journal of Economics, Vol. 35, pp. 50-68.
3. Burguet, R. y Perry M., (2007), Bribery and Favoritism by Auctioneers in Sealed-Bid Auctions, The B.E. Journal of Theoretical Economics, vol.7, (Contributions), artículo 23.
4. Celentani, M. y Ganuza J., (2002), Corruption and Competition in Procurement, European Economic Review, Vol. 43, pp. 1273-1303.
5. Compte, O., Lambert-Mogiliansky A. y Verdier T., (2005), Corruption and Competition in Procurement Auctions, RAND Journal of Economics, Vol. 36, pp. 1-15.
6. Koc, S. y Neilson W., (2008), Interim Bribery in Auctions, Economics Letters, Vol. 99, pp. 238-241.
7. Laffont, J. y Tirole J., (1991), Auction Design and Favoritism, International Journal of Industrial Organization, Vol. 9, pp. 9-42.
8. Lengwiler, Y y Wolfstetter E., (2010), Auctions and Corruption: An Analysis of Bid Rigging, Journal of Economic Dynamics and Control, Vol. 34, pp. 1872-1892.
9. Menezes, F. y Monteiro P. K., (2006), Corruption and Auctions, Journal of Mathematical Economics, Vol. 42, pp. 97-108.