Security and BER performance trade-off in wireless communication systems applications

L. Arnone^†, C. González^†, C. Gayoso^†, J. Castiñeira Moreira^‡ and M. Liberatori^‡

^† Laboratorio de Componentes, U.N.M.D.P., J. B. Justo 4302, Mar del Plata, Argentina leoarn@fi.mdp.edu.ar
^‡ Laboratorio de Comunicaciones, U.N.M.D.P., J. B. Justo 4302, Mar del Plata, Argentina casti@fi.mdp.edu.ar

Abstract — There is nowadays a strong need of designing communications systems with excellent BER performance and high levels of privacy, specially in wireless networking and mobile communications.
The transmission of encrypted information over a noisy channel presents an error propagation effect, which degrades the BER performance of the system.
In this paper, we present combined error-control coding and encryption schemes based on iteratively decoded error-control codes like LDPC and turbo codes and AES algorithm. We show that the proposed schemes strongly reduce this degradation effect.
The increase of the level of privacy is obtained by using procedures of pseudo random nature over the encoders and decoders of the error-control code.
Thus, the proposed schemes provide a given communication system with excellent BER performance and encryption capabilities.

Keywords — Iteratively Decoded Error-Control Codes. AES Algorithm.

I. INTRODUCTION

In most of the modern communication applications, like wireless LAN, privacy and reliability of the transmission are both important aims of the design. Thus, most of the channels of practical interest are those for which good encryption properties and BER performance are joint important objectives to be achieved.

Regarding encryption and security properties, it is well known the reported attacks over the encryption technique implemented in the standard 802.11 for wireless LAN, called WEP (Wired Equivalent Privacy) protocol (Brown, 2003). This requires of the implementation of a better encryption technique. In this paper we propose a combined error control coding and encryption technique. For the encryption block, we have selected AES, witch is one of the most robust encryption techniques known nowadays (Daemen and Rijmen, 1999). However, this encryption technique produces an error propagation effect, so that, efficient error control coding techniques should be also applied to counteract this effect. We have found convenient to combine this encryption algorithm with some well known efficient error control techniques, like LDPC (Gallager, 1962; MacKay and Neal, 1997) and turbo codes (Berrou et al., 1993). The final result is the design of schemes with both good privacy capability and excellent BER performance.

In Section II we show that, depending on the value of the average bit energy-to-noise power spectral density ratio Eb/N0 at which it is measured, the BER performance loss of the uncoded encrypted information transmission is from 1 to 5 dB, with respect to the uncoded and unencrypted transmission.

In Section III LDPC codes with parity check matrices H of size 128 × 256 and 1280 × 2560 are combined with the AES algorithm to show the improvement of the BER performance. In this Section we also propose some modifications based on pseudo random permutations over the structure of an LDPC code, to obtain an increase in the encryption capability of the scheme without degrading its BER performance. Section IV analyses the use of a turbo code combined with the AES algorithm. Section V presents a comparison of combined AES and efficient error control codes with respect to equivalent proposed schemes without AES. Finally, Section VI is devoted to the conclusions.

II AES ENCRYPTED UNCODED INFORMATION TRANSMISSION OVER THE AWGN CHANNEL

AES-128 (Daemen and Rijmen, 1999) is an iterative private-key symmetric block cipher that operates on a block of size L = 128 bits. The operations performed in the AES algorithm result into a non-linear transformation of the plaintext. In the case of the transmission over a noisy channel, this strong non-linearity produces an error propagation effect. Thus, few errors in a ciphered block of 128 bits result into a burst error event whose size is approximately equal to half of the length of the block. In Fig. 1 we can see a comparison between the BER performances of an uncoded AES encrypted information transmission, and uncoded and unencrypted information transmission. Transmission is performed in both cases in binary polar format and over the AWGN channel.

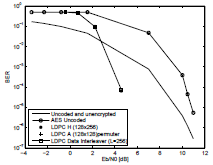
Figure 1: BER performances of the uncoded AES encrypted binary information transmission, and a combined scheme using AES encryption and a LDPC code C_LDPC(256,128), with pseudo ramdom permutation of the code vector, and with pseudo random permutation of the submatrix A.

As seen in Fig. 1, the use of the AES algorithm produces a loss in BER performance with respect to uncoded and unencrypted transmission. This suggests the addition of some error-control coding technique in order to overcome this loss. The loss in BER performance is between 1 dB to 5 dB, depending on the value of E_b/N₀ at which it is calculated.

When an error occurs over one or more of the transmitted bits of an element of the Galois Field GF (256), the de-encryption of the erroneous block of 128 bits results into a burst of errors. This can happen even when only one bit of a given element of the Galois Field GF (256) is in error. The error propagation effect produced by uncoded AES encrypted transmission can be seen in Fig. 1, where the BER performance of the uncoded AES encrypted transmission P_{be_AES}, is approximately equal to the BER performance of the uncoded and unencrypted transmission, P_be multiplied by a constant factor that we call T_AES. Thus P_{be_AES} ≈ P_be.T_AES. Simulation seen in Fig. 1 shows that T_AES ≈ 64.

Another way of measuring the error propagation effect can be seen in Fig. 2. We have simulated the transmission of uncoded AES encrypted information in blocks of 128 bits over a noisy channel. We have determined the number of errors present at the deencrypted information by observing all the 128 cases of an error pattern of one bit over the block of 128 bits. This simulation is dependant on the selected key in the AES algorithm, and on the transmitted message. The case in Fig. 2 corresponds to the use of the AES algorithm with an all-zero key, and over the all-zero message.

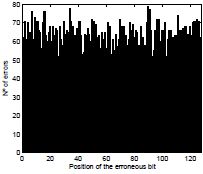
Figure 2: Number of errors generated by AES deencryption of blocks of 128 bits containing error patterns of one bit, as a function of the position of the erroneous bit.

The average numbers of errors is equal to:

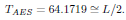(1)

It would be expected that the de-encryption of an error pattern of two or more bits can produce a burst of more errors than de-encryption of an error pattern of only one bit. However simulation seen in Fig. 1 shows that the error propagation effect produced by the de-encryption of blocks of 128 bits of uncoded AES encrypted information is always measured as a burst of T_AES ≈ 64 bits, independently of the size of the error pattern. This is also true for the weakest error pattern, which appears as the worst case. Thus, simulation in Fig. 2 confirms results obtained in Fig. 1.

Note that for low values of E_b/N₀ the BER performance of the uncoded AES encrypted binary information transmission reaches the worst value of probability of error, that is, T_AES ≈ 0.5.

III A COMBINED SCHEME USING AES ENCRYPTION AND AN LDPC CODE

LDPC codes are powerful linear block codes that are decoded using iterative decoding. For large block code lengths they perform close to the Shannon limit (Gallager, 1962; MacKay and Neal, 1997). In order to combine both techniques in transmission, the output of the AES cipher is input to an LDPC code C_LDPC (256, 128) that takes this block of m_c = 128 bits and generates a block of u = 256 bits of error-control coded information. The scheme is presented in Fig. 3 and it has been implemented with and without the data interleaver and de-interleaver.

Figure 3: A combined scheme using AES encryption and a LDPC code.

In this proposed scheme the AES algorithm is first applied to the binary information and then the encrypted output is encoded for error-correcting purposes by the LDPC code C_LDPC (256, 128). If these encoders were applied in the reverse order, at the receiver side, the decipher would operate first, but its output is a hard decision output, so that the decoding of the LDPC code would lose all the soft information obtained from the channel (Gallager, 1962; MacKay and Neal, 1997), and the efficiency of the iterative decoding would be lost. In the case of Fig. 3, the LDPC decoder operates as usual. After a given number of iterations it generates an estimate of the decoded vector, which is passed to the AES decipher as a block of 128 bits in the classic binary information format of ’1’s and ’0’s. This is a suitable input for the AES decipher. On the other hand the LDPC decoder drastically reduces the number of errors in the block of 128 bits, before this block is input to the AES decipher to be de-encrypted. This operation reduces the number of errors that the AES decipher receives, with respect to the case in which no error correction is applied, and somehow compensates the error propagation effect. However, the error propagation effect remains when the error control decoding performed by the LDPC decoder contains still some errors.

The LDPC code used in the proposed scheme is the code C_LDPC (256, 128), with a code rate R_c =1/2, that matches the format of the encrypted block of the AES algorithm. The LDPC encoder generates a block of 256 bits that contains the encrypted block and the associate redundancy. The corresponding 128 × 256 bits parity check matrix is of the form H = [A B], where the sub matrices A and B are square matrices of size 128 × 128.

The output of the LDPC encoder is a vector u = [c m_c], where m_c is the ciphertext to be encoded and c is the vector that contains the redundancy bits. On the other hand, m denotes the message vector to be transmitted and m_c = E_AES(m). Redundancy bits can be calculated as:

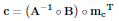(2)

so that the submatrix A should have inverse.

In a first version of this proposed scheme, the parity check matrix H is fixed. However, this part of the combined scheme can be implemented not only for error correcting purposes, but also be designed for providing to the scheme with additional levels of security.

The proposed scheme has the encryption levels of the AES algorithm, which is implemented in its standard form. We propose to take advantage of the structure of the error control block, to increase the level of privacy. A pseudo random permutation of the columns of the parity check matrix H adds an extra level of privacy to the scheme. The procedure does not involves any modification of the AES algorithm, which is used as an standard.

A problem arises because the column permutation of the parity check matrix H could result into a new parity check matrix H whose submatrix A has no inverse. We note that when the submatrix A has inverse, the permutation of its columns is equivalent to the same permutation over the corresponding bits in the code vector, in other words:

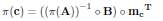(3)

In Eq. 3 π() denotes the permutation operation of the positions of the columns of the corresponding matrix, or of the bits of the corresponding vector. The permutation rule is the same in both cases. On the other hand, if the original submatrix A has inverse, the permuted submatrix π(A) also has inverse.

In order to avoid the above mentioned problem, two permutation rules could be independently applied over the submatrices A and B. However, this is not equivalent to do the same operation over the positions of the bits of the code vector. After performing the independent permutations over the submatrices A and B:

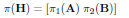(4)

and:

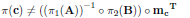(5)

We want to have a permutation operation over the parity check matrix H that can be performed by equivalently permuting the positions of the bits. Otherwise, we would need to perform a permutation over the parity check matrix H and then to calculate during encoding the inverse of the submatrix π(A), (π(A))⁻¹, in order to determine the redundant bits using Eq. 2. The calculation of the inverse of the submatrix (π(A))⁻¹ is a very costly operation in terms of computational calculations.

Therefore, it is found more convenient to apply a permutation over the positions of the bits of the code vector, instead of doing an equivalent operation over the columns of the parity check matrix H. The pseudo random permutation over the positions of the bits of the code vector is simpler and equivalent to a similar operation performed over the columns of the corresponding parity check matrix H. At the receiver side the inverse of the pseudo random permutation operates over the positions of the received samples to reorder the original code vector. This scheme is shown in Fig. 3.

During transmission, a different permutation rule is applied over every block of information. As seen in Fig. 1, this operation does not affect the BER performance of the original scheme (designed using a fixed parity check matrix H), but increases the privacy capability. The improvement of the privacy capability is measured by a factor of (2L)!, where 2L is the length of the encoded block (Castiñeira Moreira et al., 2006).

Figure 1 shows the BER performance of a scheme that uses a fixed parity check matrix H, another scheme where the submatrix A is permuted using a pseudo random rule, and a scheme where the bits of the code vector are permuted using a pseudo random rule. The three BER performances are all practically the same. Thus, an increase of 2L! = 256! 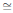8.58 × 10⁵⁰⁶ in the privacy capability of the scheme can be obtained by means of a simple pseudo random permutation of the positions of the bits of the code vector, without any degradation of the corresponding BER performance. This increased privacy capability is strong, since the block length is usually quite large.

As it is well-known, the larger is the code length of a LDPC code, the better is its BER performance (Gallager, 1962). In a new scheme a block of 10 plaintexts is first processed by the AES cipher to generate a block of 10 ciphertexts. This block, a total of m_c = 1280 encrypted bits, is taken as the input of an LDPC code C_LDPC (2560, 1280) of rate R_c =1/2 and the encoder generates as its output a block of u = 2560 bits. This block is transmitted through the channel, and then it is decoded by the iterative decoding algorithm of the LDPC code. After this, the decoded bits are deencrypted by the corresponding decipher.

The scheme seen in Fig. 3 has been implemented with and without the data interleaver and deinterleaver. The BER performance of this proposed scheme is seen in Fig. 4. The BER performance of the combined scheme using AES encryption and C_LDPC (2560, 1280) is approximately 2 dB better than the BER performance of the combined scheme using AES encryption and C_LDPC (256, 128) at a BER of 10⁻⁴ .

Figure 4: BER performances of combined schemes using AES encryption and different LDPC codes, and also turbo codes.

As seen in Fig. 4 the use of a data interleaver does not modify the BER performance of the whole scheme, but increases the privacy capability of the scheme by a factor of 20L! = 2560! 2.53 × 10⁷⁶¹⁵. Figure 4 shows that the combined AES encrypter and LDPC code, decoded with 30 iterations, has a BER that is less than 1 × 10⁻⁷ at E_b/N₀ = 3 dB.

IV A COMBINED SCHEME USING AESENCRYPTION AND A TURBO CODE WITH A RANDOM INTERLEAVER OF LENGTH L = 1280

In this proposed scheme we combine the AES algorithm with a turbo code. A group of ten blocks of AES-128 encrypted information forms a block of 1280 bits that is input to a turbo code, whose random interleaver is also of length L = 1280. The block diagram of the proposed scheme is seen in Fig. 5. The turbo code implemented has as constituent encoders RSC encoders of type (7, 5), (111, 101), and a random interleaver of length L = 1280 (Berrou et al., 1993; Castiñeira Moreira and Farrel, 2006).

Figure 5: A combined scheme using AES encryption and a turbo code.

The turbo code makes use of puncturing over the redundant bits of both encoders, so that the rate of the code is R_c =1/2. The encoder alternately transmits one of the two redundant bits, so that a given systematic bit is transmitted together with the redundant bit of the first encoder, and then the following bit is transmitted with the redundant bit of the second encoder, and so on.

It is noted that two different pseudo random data interleavers have to be applied over both, the systematic and the redundant bits, to protect the systematic information in a turbo code (Castiñeira Moreira et al., 2006).

The BER performance of this scheme is seen in Fig. 4. For low-medium values of E_b/N₀, this BER performance is better than that of the C_LDPC (2560, 1280). For higher values of E_b/N₀ this BER performance shows a floor effect characteristic of turbo codes, and it is quite close to the obtained BER in the scheme designed with the C_LDPC (2560, 1280).

In all these schemes efficient error-control coding techniques together with the AES algorithm produce a high improvement in the BER performance, in comparison with a similar scheme that transmits AES encrypted information that is not protected with error-control coding.

Thus, while uncoded AES encrypted information transmitted over the AWGN channel shows a BER performance loss that is from 1 dB to 5 dB with respect to uncoded and unencrypted transmission, the proposed schemes perform with a coding gain of around 8 dB with respect to the uncoded AES encrypted transmission.

V A COMPARISON OF THE PROPOSED COMBINED AES AND ERROR CONTROL SCHEMES WITH RESPECT TO THE SAME SCHEMES WITHOUT THE AES ALGORITHM

As seen in Section II, the transmission over a noisy channel of binary information encrypted using the AES algorithm, produces an error propagation effect. This error propagation effect can be mitigated by the use of error-control coding techniques.

By comparing efficient error-control schemes like those based on LDPC codes or on turbo codes, with equivalent versions of the proposed schemes, we measure a possible loss in BER performance produced by the use of the AES algorithm, now under the action of error-correcting codes. Results are shown in Fig. 6. As seen in Fig. 6, the error propagation effect produced by the use of the AES algorithm in the presence of error-control coding schemes is still measured as a multiplication of the number of errors by a factor that is approximately equal to T_AES, so that this effect remains the same. However, and because of the "waterfall" behavior of the BER performance of these efficient error-control coding schemes, this error propagation effect results into a loss of less than 1 dB in terms of the parameter E_b/N₀. This means that an scheme which utilizes the AES algorithm, and also some simple but very efficient permutation operations over the encrypted data, can show a very strong security capability, with a loss in BER performance of less than 1 dB, with respect to an equivalent error-control scheme without any level of privacy. Thus, in the region of E_b/N₀ between 2 − 10 dB, which is very important in many applications, and where the use of the AES algorithm produces a loss in BER performance from 2 dB to 5 dB with respect to uncoded and unencrypted transmission, the proposed schemes reduce this loss to values less than 1 dB.

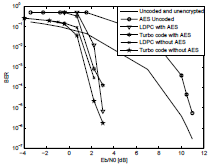
Figure 6: A comparison of the proposed combined AES and error-control coding schemes with respect to these same schemes without the use of the AES algorithm.

The proposed schemes can achieve BER performances of P_be 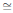7x10⁻⁶ with = E_b/N₀ 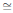3dB, whereas the AES encrypted scheme without error-control coding needs E_b/N₀ 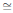11 dB to achieve the same BER performance.

It is also noted that the proposed schemes not only produce this important coding gain, but also increase the levels of security becoming very suitable for applications where privacy and efficient transmission are required. This could be the case of mobile communications.

VI CONCLUSIONS

As shown in Section II, the transmission of AES encrypted information over a noisy channel is characterized by an error propagation effect. The increase of the number of errors can be evaluated as a multiplication of the BER by a factor that is approximately half of the size of the block of the encryption process. From this point of view, BER performance and encryption are in a trade-off.

Since this effect results into a relatively high loss in the BER performance in the region of E_b/N₀ of practical interest, then it is suggested the use of efficient error-control coding schemes together with the AES algorithm, like LDPC and turbo codes, especially when high levels of privacy is required in a transmission over very noisy channels. This is so because AES encrypted information not protected against noise requires a quite large amount of E_b/N₀ to perform at acceptable values of BER in practice.

In this paper we have presented combined schemes with the aim of both increasing levels of privacy of the whole scheme, in addition to that provided by classic encryption techniques like the AES algorithm, and reducing the loss in BER performance produced by the application of this encryption algorithm, to a very low value of less than 1 dB.

Combined AES and efficient error-control schemes can perform at a BER of 7×10⁻⁶ with E_b/N₀ 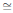3 dB, whereas this BER requires E_b/N₀ 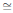11 dB for the uncoded and unencrypted case.

Therefore, the proposed schemes can perform with a loss of less than 1 dB with respect to their equivalent error-control coding schemes, in which AES is not implemented. The acceptance of this relatively low loss provides the whole scheme with a very high level of privacy, which is the level of encryption of the AES algorithm increased by the modification of the structure of the error-control coding encoders and decoders. The robustness of the standard AES is affected by a factor that can be(2L)! or (20L)!, depending on the selected scheme.

REFERENCES
1. Berrou, C., A. Glavieux and P. Thitimajshima, "Near Shannon limit error-correcting coding an decoding: Turbo codes," IEEE Internacional Conference on Communications, 2, 1064-1070 (1993).
2. Brown, B., "802.11: the security differences between b and i ," IEEE Potentials, 22, 23-27 (2003).
3. Castiñeira Moreira, J. and P. G. Farrell, Essential off Error-Control Coding, John Wiley and Sons, England (2006).
4. Castiñeira Moreira, J., D. Petruzzi, M. Liberatori and B. Honary, "Trellis hopping turbo coding," IEE Proceedings - Communications, 153, 966-975 (2006).
5. Daemen, J. and V. Rijmen, "AES Proposal: Rijndael. Document version 2," IRE Trans. Information Theory. NISTs AES home page, http://www.nist.gov/aes (1999).
6. Gallager, R.G., "Low Density Parity Check Codes," IRE Trans. Information Theory, IT-8, 21-28 (1962).
7. MacKay, D.J.C. and R.M. Neal, "Near Shannon limit performance of low density parity check codes," Electronics Letters, 33, 457-458 (1997).

Received: October 18, 2007.
Accepted: October 9, 2008.
Recommended by Guest Editors D. Alonso, J. Figueroa, E. Paolini and J. Solsona.