Partial differential equations for missing boundary conditions in the linear-quadratic optimal control problem

V. Costanza^† and C.E. Neuman^‡

^† INTEC (UNL-CONICET), Güemes 3450, 3000 Santa Fe, Argentina
tsinoli@ceride.gov.ar
^‡ Dep. de Matemática (FIQ), Universidad Nac. del Litoral, Sgo. del Estero 2829, 3000 Santa Fe, Argentina
ceneuman@fiqus.unl.edu.ar

Abstract — New equations involving the unknown final states and initial costates corresponding to families of LQR problems are found, and their solutions are computed and validated. Having the initial values of the costates, the optimal control can then be constructed, for each particular problem, from the solution to the Hamiltonian equations, now achievable through on-line integration. The missing boundary conditions are obtained by solving (off-line) two uncoupled, first-order, quasi-linear, partial differential equations for two auxiliary n × n matrices, whose independent variables are the time-horizon duration T and the final-penalty matrix S. The solutions to these PDEs give information on the behavior of the whole two-parameter family of control problems, which can be used for design purposes. The mathematical treatment takes advantage of the symplectic structure of the Hamiltonian formalism, which allows to reformulate one of Bellman's conjectures related to the "invariant-imbedding" methodology. Results are tested against solutions of the differential Riccati equations associated with these problems, and the attributes of the two approaches are illustrated and discussed.

Keywords — Optimal Control. Linear-quadratic Problem. First Order PDEs. Boundary-value Problems. Riccati Equations.

I. INTRODUCTION

The linear-quadratic regulator (LQR) problem is probably the most studied and used in the state-space optimal control literature. The main line of work in this direction has evolved around the algebraic (ARE, for infinite-horizon problems) and differential (DRE, for finite-horizon ones) Riccati equations. When expressed in 2n-phase space, i.e. introducing the costate (the spacial derivative of the value function), the dynamics of the optimal control problem takes the form of the classical Hamilton's equations of fundamental Physics.

Since early sixties, Hamiltonian formalism has been at the core of the development of modern optimal control theory (Pontryagin et al., 1962). When the problem concerning an n-dimensional system and an additive cost objective is regular (Kalman et al., 1969), i.e. when the Hamiltonian of the problem can be uniquely optimized by a control value u⁰ depending on the remaining variables (t,x,λ), then a set of 2n ordinary differential equations (ODEs) with a two-point boundary-value condition, known as Hamilton's (or Hamiltonian) equations (HE), has to be solved. This is often a rather difficult numerical problem. For the linear-quadratic regulator (LQR) with a finite horizon there exist well known methods (see for instance Sontag, 1998) to transform the boundary-value problem into an initial-value one. In the infinite-horizon, bilinear-quadratic regulator and change of set-point servo, there is a recent attempt to find the missing initial condition for the costate variable, which allows to integrate the equations on-line with the underlying control process (Costanza and Neuman, 2006).

Hamiltonian systems (modelled by a 2n-dimensional ODE whose vector field can be expressed in terms of the partial derivatives of an underlying "total energy" function -called "the Hamiltonian"-, constant along trajectories), are key objects in Mathematical Physics. The ODEs for the state and costate of an optimal control problem referred above constitute a Hamiltonian system from this general point of view. Richard Bellman has contributed in both fields, but was particularly interested in symplectic systems coming from Physics (see for instance Abraham and Marsden, 1978) when he devised a partial differential equation (PDE) for the final value of the state x(t_f)=r(T,c) as a function of the duration of the process T=t_f-t₀, and of the final value imposed to the costate λ(t_f)=c (one of the boundary conditions, the other being the fixed initial value of the state x(t₀)=x₀, see Bellman and Kalaba, 1963). Bellman exploited in that case ideas common to the "invariant imbedding" numerical techniques, also associated with his name.

In Costanza (2008) the invariant imbedding approach is generalized and proved for the one-dimensional nonlinear-quadratic optimal control situation, where the final value of the costate depends on the final value of the state, i.e. c=c(r). The procedure followed in this proof induces another PDE for the initial value σ of the costate λ(t₀), which was actually the main concern from the optimal control point of view. The first-order quasilinear equation for σ developed here is new. It can be integrated after the PDE for the final state ρ (independent of σ) has been solved. The "initial" condition for σ depends on the final value of the state and the weight matrix S involved in the quadratic final penalty x'(T)Sx(T). Therefore it seems more natural to consider here (T,S) as the independent parameters of the family of control problems under consideration. Having found the solution σ(T,S) the HE can be integrated for each particular value of the parameters. However, the whole curves ρ(.,S), σ(.,S) can be useful in real time, as a kind of safeguard against unexpected departures of the numerical solution to the HE. Normal solutions to Hamiltonian systems are unstable near equilibrium, a characteristic inherent to the spectrum of their linearizations (if λ is an eigenvalue of the linear approximation, so is -λ, see Abraham and Marsden, 1978).

In what follows, and after some notation and general characteristics of the problem are exposed in section II, the main PDE equations for the missing boundary conditions are proved in section III. Numerical validations and illustrations are provided in section IV, and the whole approach discussed in the Conclusions. An Appendix is added to substantiate the general set-up valid for the nonlinear case, and the corresponding equations for the one-dimensional case reviewed (see Costanza, 2008; for additional details).

II. FORMULATION OF THE PROBLEM

The classical finite-horizon formulation of the "LQR problem " for finite-dimensional, constant systems, attempts to minimize the (quadratic) cost

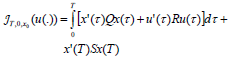(1)

with respect to all admissible control trajectories u(.) of duration T applied to some fixed, deterministic (linear) plant; i.e. those affecting the 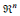- valued states x of the system through some dynamic restriction

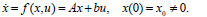(2)

The (real, time-constant) matrices in Eqs. (1,2) will have the following properties: Q,R,S symmetric, Q,S≥0, R>0, A∈M_n(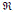), B is n × m. The expression under the integral is usually known as the "Lagrangian " L of the cost, i.e.,

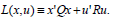(3)

The Hamiltonian of such a problem, namely the 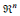××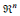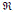→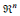function defined by

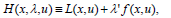(4)

is known to be regular, i.e. that H is uniquely minimized with respect to u by the control value

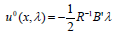(3)

(in this case, independent of x), which is usually called "the H-minimal control. " The "Hamiltonian " form of the problem (see for instance Sontag, 1998) requires then to solve the two-point boundary-value problem

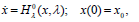(6)

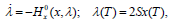(7)

where H⁰(x,λ) stands for H(x,λ,u⁰(x,λ)), and 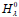, 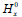for the column vectors with i-components 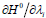, 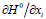respectively, which here take the form

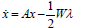(8)

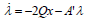(9)

with W≡BR^-1B'. There are no general solutions to boundary-value problems. In the following section a novel approach to overcome this difficulty, by imbedding the individual situation into a two-parameter family of similar problems, will be presented and substantiated.

III. EQUATIONS FOR THE MISSING BOUNDARY CONDITIONS

For the nonlinear-quadratic one-dimensional case two quasilinear first-order PDEs (53, 55) have been found (see the Appendix), one for each of the missing boundary conditions of the problem, namely the final state x(T) and the initial costate λ(0). Unfortunately such PDEs can not be extrapolated to higher dimensions in an obvious way. However, the immersion of the problem into a two-parameter (T,S) family is still fruitful, as will be evident from what follows.

It is well known that the LQR problem has a unique solution via the Riccati differential equation (DRE)

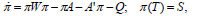(10)

leading to the optimal feedback

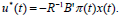(11)

An alternative classical approach (see for instance Bernard, 1972) transforms the original boundary-value problem into an initial-value one, by introducing the following auxiliary objects:

(i) the Hamiltonian matrix H,

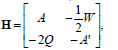(12)

(ii) and the augmented Hamiltonian system (a linear matrix ODE) defined for two n×n matrices X(t), Λ(t), t∈[0,T] through

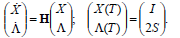(13)

The solution to system (13) is

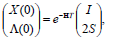(14)

and since in this case Eqs. (6-7) read

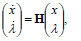(15)

the missing boundary conditions can be explicitly found

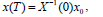(16)

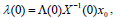(17)

(see Sontag, 1998, for the invertibility of X and other details). Actually, the whole solution to DRE can be recuperated from the solution to the augmented system (13), namely

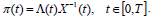(18)

However it is desirable to count with the missing boundary values for different values of the parameters T,S without solving either the DRE or the augmented system described above. A method to solve the whole (T,S)-family of LQR problems (with common A, B, Q, R, x₀ values) was then developed. To be precise, just the case with S=sI, with s≥0 will be exposed, the extension to non-scalar matrices being more operationally involved but not conceptually different. Nevertheless, the preset set-up is pertinent to many applications. From now on, the notation for the relevant missing boundary values and matrices will be

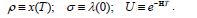(19)

The method starts by defining, for each particular (T,S)-problem

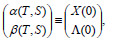(20)

which allows to rewrite Eq. (14) in the form

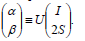(21)

Since the subjacent Hamiltonian system is linear, solutions depend smoothly on parameters and initial conditions, and then derivatives of Eq. (21) with respect to (T,S) can be taken

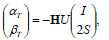(22)

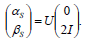(23)

Now, by partitioning in the obvious way

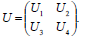(24)

Then, Eq. (23) reads

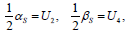(25)

which combined with Eq. (21) gives

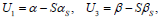(26)

and then, by inserting these results in Eq. (22), the following (main) relations are obtained

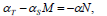(27)

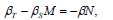(28)

where M≡A'S+SA+Q-SWS, N≡A-WS.

Boundary conditions for a process of zero horizon are imposed in view of Eqs. (20, 16, 17), i.e.

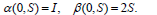(29)

The desired values of the missing values for the state and costate, for any (T,S)-problem may then be recuperated from the solutions α and β through

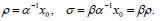(30)

It can be easily checked that the PDEs and boundary conditions (53-54, 55-56), whose validity is already known in the one-dimensional nonlinear case (see the Appendix), are also verified by the scalar version of Eqs. (30), namely

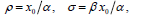(31)

(α is always nonzero), provided that α, β satisfy Eqs. (27, 28, 29).

Two other possible reformulations of these equations for linear n-dimensional systems may be explored (with theoretical rather than practical purposes): the scalar (internal) product

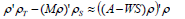(32)

and the matrix (external product) form:

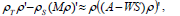(33)

(and the corresponding analogous equations for σ). Both proved to be insufficient to predict the desired values of ρ, σ, so it was necessary to generalize to matrix equations for α and β in order to solve the general linear problem. In the next section some results of numerical calculations involving the solutions to Eqs. (27,28) are examined and compared against the DRE approach.

IV. NUMERICAL CALCULATIONS AND ADDITIONAL VALIDATIONS

Equations (27, 28, 29) were solved numerically with standard software in several cases, and the solutions were tested to verify the following identities stemming from the symplectic structure of the problem (see Katok and Hasselblatt, 1999; Jacobson, 1974)

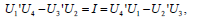(34)

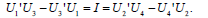(35)

Also, to illustrate the theoretical results, some components of the solutions (ρ, σ) for the linear system with matrices

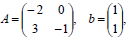(36)

subject to the quadratic Lagrangian defined by matrices

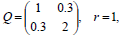were plotted for the range (T,S)∈[0,1]×[0,1] in Figs. 1 and 2.

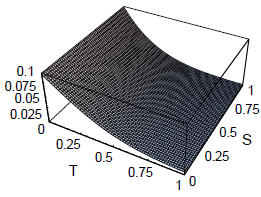
Figure 1: First component ρ₁(T,s) of final state value calculated from matrix α.

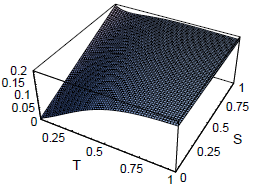
Figure 2: First component σ₁(T,s) of initial costate, from matrices α and β.

The results were also compared with the DRE solution for several intermediate (T,S)-problems, which showed almost no difference, as can be seen in Figure 3.

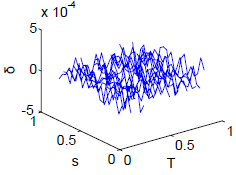
Figure 3: Difference between ρ₁ calculated from matriz α and by solving de DRE.

The time trajectories were also calculated from the initial conditions σ(0.5,sI) for several values of s, just to illustrate how the regulation capacity (the approaching to (0,0)) increases with increasing final penalty (Fig. 4). It is also interesting to observe that the two components of the state tend to the origin, since the optimal LQR control is stabilizing, but they do not decrease monotonically as the results in Fig. 1 may suggest. Actually, for small final penalty (s=0.25), the second component first grows from its initial value (0.1), and only after some time it heads towards equilibrium (Figs. 4 and 5).

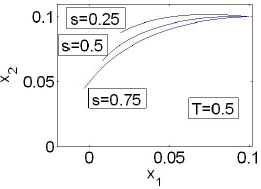
Figure 4: Trajectories in phase space.

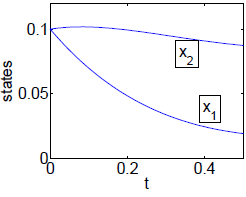
Figure 5: States time-trajectories for small final penalty (s=0.25).

For this example both members of relations (32) and (33) were also evaluated. An agreement of the order 10^-3 was observed. Since the values of the variables involved in the calculations are relatively small, firm hypotheses on the soundness of Eqs. (32, 33) can not be raised yet.

V. CONCLUSIONS

New equations to transform the classical two-point boundary-value ODE system associated with the Hamiltonian formulation of finite-horizon LQR problems, into an initial-value set-up with unique solution, have been derived, solved and illustrated. The approach is based on invariant-imbedding ideas, although the original Bellman methodology resulted somehow inadequate in this case. By solving two matrix, quasilinear, first-order PDEs for auxiliary variables α, β proposed here, the missing boundary conditions are effectively recuperated after simple manipulations. Actually, the auxiliary variables are found for a two-parameter family of LQR problems posed for fixed plant dynamics and trajectory costs, but with variable final penalty and horizon spans. This immersion allows a whole range of (T,S)-problems to be assessed by looking at the final reachable state ρ(T,S) and the associated marginal cost σ(T,S).

It is remarkable that the solution to a twice-infinite family of LQR problems requires little numerical effort, roughly similar to the one involved in running the associated DRE\ for just one individual situation. The solution for a range of (T,S)-values provides design information, useful when flexible choice of the parameters to improve performance is present.

The soundness of this approach for linear plants seems also promising in suggesting an algorithm to solve multidimensional nonlinear problems with regular Hamiltonians, even allowing for more general Lagrangians than those described by quadratic forms. This idea is already under development.

APPENDIX: PDES FOR THE MISSING BOUNDARY CONDITIONS IN THE ONE-DIMENSIONAL NONLINEAR-QUADRATIC CASE

It is assumed that for each combination of parameters (T,S) the two-point boundary-value problem posed by Eqs. (6-7) has a unique solution, varying smoothly with smooth changes in parameters. For the (in general nonlinear) system

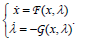(37)

it will be assumed to exist a smooth flow Φ: ×O→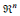, with O denoting some sufficiently large open set in 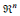×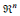, such that Φ(t,x,λ) will render the values of the state and costate at time t along the trajectory starting (when t=0) at the generic value (x, λ). The following notation indicates that the two “components” of the flow, referring to the state (denoted by Φ₁ below) and the costate (denoted Φ₂), each in 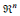, will be considered separately

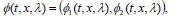(38)

and, accordingly, the following identities become clear

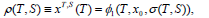(39)

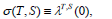(40)

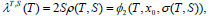(41)

where (x^T,S(.),λ^T,S(.)) is the optimal trajectory corresponding to a fixed horizon duration T and a fixed penalty weight, and the point in (.) stands for the independent variable time t∈[0,T].

By taking partial derivatives with respect to T in Eq. (39) (the notation D₁ = ∂/∂T, and similarly for other partial derivatives, is adopted when clarity seems necessary),

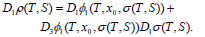(42)

Since the existence of the flow implies

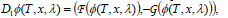(43)

i.e. it “verifies” the original ODEs (37); then, at the final time T,

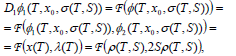(44)

which will be written simply as

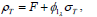(45)

with F standing for

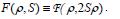(46)

Now, the derivative of Eq. (39) with respect to S gives

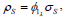(47)

and repeating the procedure (∂/∂T,∂/∂S) with Eq. (41) renders

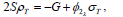(48)

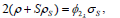(49)

where G is consistently defined as

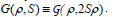(50)

Formally, from Eqs. (45) and (47), 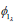can be eliminated; and so can from Eqs. (48) and (49); to obtain, respectively,

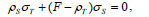(51)

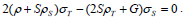(52)

Therefore, in order for the problem to have a nontrivial solution, the determinant of the augmented system must be null, i.e.

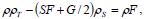(53)

which is a first-order, quasi-linear PDE for ρ, that can be integrated independently from σ, with the boundary condition

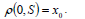(54)

Also, from Eqs. (51) and (52) it follows that

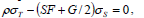(55)

also a linear, but homogeneous, first order PDE, subject to the boundary condition

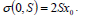(56)

REFERENCES
1. Abraham, R. and J.E. Marsden, Foundations of Mechanics, Second Edition, Benjamin Cummings Reading, Massachusetts (1978).
2. Bellman, R. and R. Kalaba, "A note on Hamilton's equations and invariant imbedding, " Quarterly of Applied Mathematics, XXI, 166-168 (1963).
3. Bernard, P., Introducción a la Teoría de Control Óptimo, Cuadernos del Instituto de Matemática "Beppo Levi, " 4, UNR, Rosario (1972).
4. Costanza, V., "Finding initial costates in finite-horizon nonlinear-quadratic optimal control problems, " Optimal Control Applications & Methods, 29, 225-242 (2008).
5. Costanza, V. and C.E. Neuman, "Optimal control of nonlinear chemical reactors via an initial-value Hamiltonian problem, " Optimal Control Applications & Methods, 27, 41-60 (2006).
6. Jacobson, N., Basic Algebra I, W.H. Freeman and Co., San Francisco (1974).
7. Kalman, R.E., P.L. Falb and M.A. Arbib, Topics in Mathematical System Theory, McGraw-Hill, New York (1969).
8. Katok, A. and B. Hasselblatt, Introduction to the Modern Theory of Dynamical Systems, Cambridge University Press, Cambridge, U.K. (1999).
9. Pontryagin, L.S., V.G. Boltyanskii, R.V. Gamkrelidze and E.F. Mischenko, The Mathematical Theory of Optimal Processes, Wiley, New York (1962).
10. Sontag, E.D., Mathematical Control Theory, Springer, New York (1998).

Received: October 18, 2007.
Accepted: July 2, 2008.
Recommended by Guest Editors D. Alonso, J. Figueroa, E. Paolini and J. Solsona.