Optical pulse compression by photonic devices

P.A. Costanzo-Caso^†, C. Cuadrado^†, R. Duchowicz^† and E. Sicre^‡

^† Centro de Investigaciones Ópticas (CIOp), Camino Centenario y 506, La Plata (1900), Argentina.
Facultad de Ingeniería, UNLP.
pcostanzo@ing.unlp.edu.ar, ricardod@ciop.unlp.edu.ar
^‡ Universidad Argentina de la Empresa (UADE), Lima 717, Buenos Aires (C1073AAO), Argentina
esicre@uade.edu.ar

Abstract — By combining phase modulation and dispersive transmission on a given time-varying in-put signal, we propose an optical device for produc-ing ultrashort light pulses of high optical power. We derive the relationship between the required proper-ties of the input signal and the device parameters in order to optimize the energy concentration in the output optical pulses. The high-order aberrations effects of the time lens which perform the phase modulation are considered. Besides, the differences on the obtained pulse shape when the input signal has a gaussian or a super-gaussian envelope are illus-trated. Finally, some numerical simulations are shown which illustrate the feasibility of the method.

Keynotes — Optical Fiber Devices. Optical Pulse Compression.

I. INTRODUCTION

The development of techniques for the analysis and syn-thesis of ultrashort optical pulses has become a subject of the most importance in the field of optical communi-cations, photonic signal processing and ultrafast optics. From the spatial-temporal duality theory (Kolner, 1994; Papoulis, 1994, Bennett and Kolner, 2001; Van Howe and Xu, 2006) well-known concepts and experiments developed in the framework of spatial image processing can be transferred to the temporal domain thereby pro-viding new ways for analyzing and processing temporal optical signals. Among several applications, the tempo-ral Talbot effect (Azaña and Muriel, 2001; Azaña and Chen, 2003; Cuadrado-Laborde et al., 2006; Chantada et al., 2006) and others similar techniques (Torres-Company et al., 2006; Komukai et al., 2005) were im-plemented in order to produce periodic pulse trains with different repetition rates. The basic components of these temporal devices are dispersion lines, such as optical fibers (OF) or linearly chirped Bragg gratings (LCFG), and time lenses which are basically quadratic phase modulators.

In this paper, we analyze the conditions to be achieved by a photonics device combining phase modu-lation and dispersive transmission on a certain time-varying input signal for producing ultrashort light pulses with high optical power. Same as periodicity of the in-put signal assures selfimaging when the Talbot condi-tion is satisfied, energy concentration requires a photonic device acting on the input signal in a similar way as a spatial "diffractive" lens focuses light energy.

In Section II we derive the conditions to be fulfilled by the several parameters associated with the setup here proposed, for obtaining well conformed light pulse of high-energy. Besides, we analyze the effect on the pulse shape of the combined action of third- and fourth-order aberrations of the time lens, and the detuning from the proper dispersion value of the dispersive media. In Sec-tion III we analyze the system implementation feasibil-ity with real devices (phase modulators and dispersive lines) and the quality of the pulses generated are dis-cussed. In Section IV the pulse generation is analyzed by considering a laser source where the envelope of the emitted signal is a gaussian or a super-gaussian func-tion. Finally, in Section V we present the conclusions of this work.

II BASIC THEORY

Let us consider that the input signal to the system to be analyzed is given by the output of either a continuous (CW) or a pulsed laser centered at the angular frequency ω0, but modulated with a signal that has a linear fre-quency variation. Thus, its complex envelope can be written in a general form as

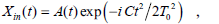(1)

where we denote as A(t) the baseband amplitude (con-tinuous or pulsed) of the input signal, T0 is related with the temporal duration of Xin(t), and C is a chirp parame-ter which takes into account a linear frequency varia-tion. This input signal is successively phase modulated by a temporal lens and transmitted through a first-order dispersion line for producing the output signal X_out(t). The phase function associated with the optical modula-tor can be written as φ(t) = Φ₂₀ t2/2 + Δφ(t), where Φ₂₀ is the quadratic modulation factor responsible of the lens action and Δφ(t) is the deviation term (which includes higher orders terms in the Taylor expansion of φ(t)) which can be treated in a similar way as the aberration function is analyzed in spatial imaging. Regarding with the dispersion line, it has associated a quadratic-phase spectral response centered at the mean frequency ω0 of the input signal, with a second order parameter Φ₂₀. For arbitrary values of the device parameters Φ₂₀ and Φ₂₀, the baseband equivalent amplitude of the output signal becomes

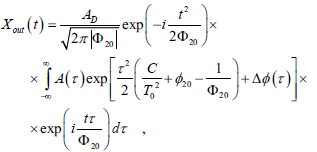(2)

where A_D is the modulus of the transfer function associ-ated with the dispersion line.

In any of the two situations (pulse or CW), the total duration of X_in(t), limited by A(t), is restricted by the time aperture TA of the time lens, in such a way that the actual duration should be lower that the TA. From Eq. (2), in order to obtain an energy concentration in the form of a sharp pulse, the quadratic phase inside the integral should be zero. If we consider that the aberra-tion term Δφ(t) is zero, the following relation should be fulfilled by the dispersion parameter

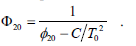(3)

Under the condition of Eq. (3), the output ampli-tude is basically proportional to the Fourier transform of A(t). By this reason, for simultaneously minimizing the temporal duration of X_out(t) and concentrating most of the optical power of X_in(t) in the main pulse, A(t) should be ideally given by a continuous or a sinusoidal signal. Thus, the output amplitude becomes

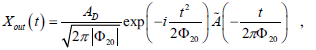(4)

where Ã(.) means the Fourier transform of A(.). Thus, an ultra-short pulse with a high optical intensity can be produced depending on the shape, chirp and duration of the input signal, whenever the system parameters satisfy Eq. (3).

Let us now consider the effect of the higher orders terms in the Taylor expansion of φ(t), i.e., we analyze the phase modulation function φ(t) = φ₂₀t²/2+φ₃₀t³/6+φ₄₀t⁴/24, which takes into account the cubic and quartic modulation factors φ₃₀ and φ₄₀. Besides, we analyze the effect of a detuning from the condition of Eq. (3) in the form Φ₂₀ = 1/(φ₂₀−C/T₀²) ± ΔΦ, due to any variation of the quadratic dispersion term. In this case, the term in Eq. (2) that originates the desired energy concentration can be rewritten as

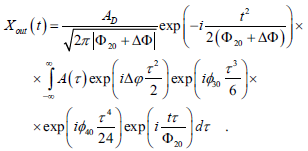(5)

We initially select TA small enough as to neglect the effect of φ₄₀. In this case, the output amplitude, as given by Eq. (5), mathematically coincides with the amplitude u(L; t) obtained when a pulse a initial shape u(0; t) is propagated by a certain distance L inside an optical fiber, having dispersion parameters β₂ and β₃ (Agrawal, 2001). Thus, Eq. (5) could be rewritten as: X_out(t) = K×exp(−it²/2Φ₂₀)×u(L;-t/Φ₂₀), being u(0; t) the input "equivalent" transmitted pulse given by 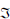^-1{A(τ)} (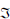^-1 denotes the inverse Fourier transform).

The equivalent dispersion parameters are related with the device parameters through: β₂L = 2Δφ and β₃L = φ₃₀. By taking into account that higher-order dis-persion effects become relevant in fiber pulse transmis-sion only if 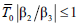(being 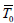a measure of the pulse width) the output signal significantly deviates from the result of Eq. (2) whenever 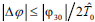. In this expression, 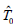represents the mean time width of u(0; t). Same as it is observed in the dispersive trans-mission of its "equivalent pulse", X_out(t) changes from a symmetrical sharp peak (assuming that A(t) is indeed symmetric) to a non-symmetric shape exhibiting an os-cillating structure on one side. For the case of φ₃₀ > 0, the oscillations occur in the trailing edge of the output pulse. On the other hand, if only the φ₄₀ contribution is relevant, spherical aberration is observed (same as in spatial imaging) originating two effects (Van Howe, 2006): i) The pulse width is increased as compared with the ideal, non-aberrated situation of Eq. (4); and ii) The dispersion parameter Φ₂₀ required to produce the sharp pulse slightly varies from the value that is obtained from Eq. (3). This last effect is related with the well-known focal-shift that is originated by the fourth-order aberra-tion. These results will be illustrated in the next section.

III. IMPLEMENTATION FEASIBILITY

The achieved results will be illustrated with some nu-merical simulations. We will compare the results ob-tained using an ideal modulator with those obtained using an electro-optic modulator (EOM) fed with a si-nusoidal phase signal. Besides, we also analyze both, the pulse conformation for a varying dispersion parame-ter and the effects which are to be present if there exist a detuning in the condition given by Eq. (3).

The input signal envelope was selected as A×rect(t/T₀)cos[2π(f_p+Δf_pt) t], being A² the continuous optical power and the rect(.) function limits the signal temporal duration to T₀ = 4 ns. The linear frequency variation has an initial value f_p = 16.7 GHz and a change rate Δf_p = 2.5×10¹⁸ Hz². By selecting Φ₂₀ = 10¹⁸ Hz² the sharp pulse condition is achieved when the dispersion parameter becomes Φ₂₀ = Φ₂₀^(p) = 3.085×10⁴ ps². Under this condition, the normalized output intensity when an ideal modulator is used (where the phase modulation function is φ(t) = Φ₂₀ t²/2 and TA = T₀ = 4 ns) is shown in Fig. 1(a). As it is expected from Eq. (3), with A(t) = A×rect(t/T₀), the output optical power has a sinc²(.) function shape, containing the main lobe around 50% of the input energy and being the FWHM (full wave half medium) width of the pulse δt_out ≅ 48 ps. In order to illustrate the required accuracy in the dispersion parameter selection, we also show the output intensity when a ±10% detuning of Φ₂₀^(p) is considered.

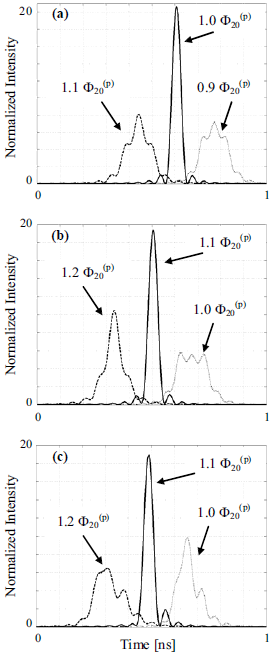
Fig. 1. Output optical power for three different time lens (maintaining constant φ₂₀ = 10¹⁸ Hz²) having the term Φ₂₀ as parameter. (a) For an ideal free-aberrated time lens (TA=4 ns) with Φ₂₀=Φ₂₀^(p)=3.085×10⁴ ps², Φ₂₀ = 1.1×Φ₂₀^(p) and Φ₂₀ = 0.9×Φ₂₀^(p). (b) An EOM with phase modulation φ(t) = cos(2π160 MHzt). In this case, due to the spherical aberration shift-effect which is present, the output pulse is formed for Φ₂₀ = 1.1×Φ₂₀^(p). (c) An EOM with phase modulation φ(t) = cos(2π160 MHz t+π/3). In this case, the pulse is formed for Φ₂₀ = 1.1×Φ₂₀^(p) again, but this becomes slightly non-symmetric (see the side-lobes).

Next, for illustrating the aberrations effect in the pulse shape, we consider a real temporal lens given by an EOM having a phase modulation function φ(t) = cos(ω_m t), with f_m = ω_m/2π = 160 MHz. It should be taken into account that this modulation function has associated the same quadratic coefficient Φ₂₀ = 10¹⁸ Hz² as in the previous ideal case but, due to the value of ωm, its free-aberrations TA is restricted to 1 ns (<T₀ = 4ns). As the cosine function is not time-shifted, there is only present φ₄₀ as lens aberration. Now, the output intensity is shown in Fig. 1(b) and it can be seen that the maximum output is produced for Φ₂₀ = 1.1×Φ₂₀^(p), as it would be expected due to the spherical aberration "shift effect". Regarding with the pulse shape, the main lobe of the pulse is practically the same as in the ideal case and the side-lobes are slightly increased. Finally, we consider the more general electro-optic modulation function φ(t) = cos(ω_mt + Δφ₀), where Δφ₀ is an arbitrary phase shift. As the cosine function is now shifted, both coefficients φ₃₀ and φ₄₀ are present introducing another lens aberration contribution. In this case, the output intensity is shown in Fig. 1(c) for Δφ₀ = π/3, and it can be observed that due to the combined action of both aberrations, the complete pulse is non-symmetrical (see the side-lobes) and it is again formed at Φ₂₀ = 1.1×Φ₂₀^(p). However, it can be observed that the main lobe remains almost unchanged in any of the three cases. In order to better illustrate the high energy pulse formation, a 3D display of the output intensity is shown in Fig. 2(a) for a continuously varying Φ₂₀, from zero to its maximum value. For Φ₂₀=Φ₂₀^(p)=3.085×10⁴ ps² a very sharply pulse with a high amplitude is conformed (where Eq. (3) is satisfied), while for Φ₂₀ > Φ₂₀^(p) the pulse intensity rapidly decreases becoming its value negligible as compared with the obtained maximum value. From Fig. 2(a), the maximum output intensity results around twenty times the input intensity, for the selected device parameters.

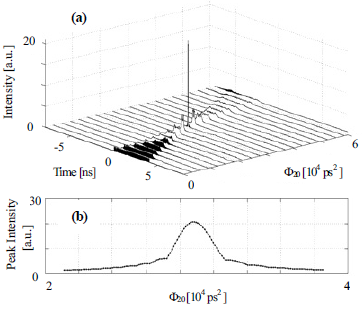
Fig. 2. (a) Three-dimensional display of the output optical power, corresponding to the EOM of Fig. 1(c), which is obtained for a continuously varying Φ₂₀. The high energy pulse conformation is achieved in a well defined condition. (b) Dependence of the maximum output intensity with the dispersion parameter.

Finally, we analyze the behaviour of the maximum output intensity when a detuning in Eq. (3) is present due to a variation of the dispersion parameter Φ₂₀. From Fig. 2(b), it can be observed that, by admitting a 50% decreasing of the maximum intensity, it corresponds to a relative variation of the dispersion parameter of ∼ 8%, and an absolute variation of 0.25x10⁴ ps², which in terms of length of standard optical fiber it is equivalent to 100 km approximately. Therefore, in order to imple-ment the dispersive line, the appropriate photonic device should be a LCFG or a photonic crystal fiber, since the resulting standard optical fiber length is large enough and the nonlinear effects should be considered (Hanna et al., 2005).

IV. SEMICONDUCTOR LASER PULSES COM-PRESSION

In the previous sections we found the theoretical condi-tions for obtaining an ultrashort high pulse when the input is a bandpass signal with a linear frequency modula-tion. Now, we analyze the system performance when theinput signal is obtained from a real semiconductor laser which is internally modulated. This optical enve-lope signal has a considerable frequency chirp and it can be expressed as

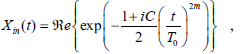(6)

where the envelope shape is a gaussian or super-Gaussian function (depending if m = 1 or m = 2; 3; ..., respectively), and the chirp parameter is estimated from experimental measurements to a value C 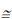-6 (Agrawal, 2001). The output signal can be analytically obtained when the coefficient is m = 1, but for m > 1 the solution can be only obtained by numerical simulation.

Let us consider that the input signal is given as in Eq. (6), with m = 1, and it is successively phase modu-lated and propagated in a dispersive line, in such way that the condition given by Eq. (3) is satisfied. There-fore, the output signal can be written as

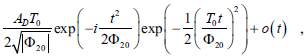(7)

where o(t) is a low amplitude undesirable term. It is possible to evaluate the broadening factor as the relation between the input and output pulse standard deviation, which is given as

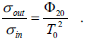(8)

Now, in order to show the numerical results and to analyze the performance of the system, we have consid-ered two input signals: the first one is given by a gaus-sian pulse, and the second one is given by a super-gaussian pulse, where m = 3 was selected. Figure 3 (a) and (b) show the gaussian and super-gaussian input sig-nals, respectively, where C = -6 and T₀ = 16.67 ps were selected. Can be observed that the super-gaussian pulse shape have a steeper leading and trailing edges. Same as in previous section, we have selecting Φ₂₀ = 10¹⁸ Hz² for the phase modulation factor of the EOM. Thus, the dis-persion factor for getting the pulse compression, from Eq. (3), is Φ₂₀^(p) = 46.294 ps².

Fig. 3. Typical characteristics of the input and output pulses: (a) and (b) normalized input amplitude for: a gaussian and a super-gaussian chirped pulse, respectively; (c) and (d) normalized output intensity when the condition given as in Eq. (3) is satisfied; (e) and (f) pulse conformation evolutions.

Figures 3 (c) and (d) show the output intensities obtained when the input signals become a gaussian and a super-gaussian envelope, respectively. It can be ob-served a temporal pulse compression effect and an in-creasing of the energy level signal for both input sig-nals. However, this last effect is more noticeable for the case of a gaussian input. The broadening factor, calcu-lated fron Eq. (8), results to be 0.1667 and the amplifi-cation intensity level becomes 1.5. Figures 3 (e) and (f) show the pulse time evolution when it is propagated through the dispersive line. In each figure it can be clearly observed the dispersion value for which the pulse compression effect is reached. Besides, it can be seen the formation of an undesired secondary pulse of lower amplitude which is given by the term o(t) in Eq. (7).

V. CONCLUSIONS

In this work we have analyzed a simple technique for compressing optical pulses, by properly combining dis-persive propagation and phase modulation. The system performance was illustrated with some numerical simu-lations. The effect of both, the time lens aberrations and a possible variation of the amount of required disper-sion, were analyzed and illustrated. The deviations of the ideal conditions were also considered by introducing the action of real electro-optical modulators and by choosing an input signal that resembles the pulse emis-sion of most semiconductor lasers. The proposed tech-nique of pulse compression can be applied for minimiz-ing intersymbol interference (ISI) in high speed com-munication systems and for obtaining a TDM channel with a large transmission rate.

ACKNOWLEDGEMENTS
This work was supported by Consejo Nacional de Inves-tigaciones Científicas y Técnicas (CONICET- PIP 6156/05), Facultad de Ingeniería de la Universidad Na-cional de La Plata (UNLP - Project I106) and Agencia Nacional de Promoción Científica y Tecnológica (ANPCyT - PICT 38289). PACC is fellowship of CONICET.

REFERENCES
1. Agrawal, G.P., Nonlinear Fiber Optics, 3rd. ed., Academic Press, (2001).
2. Azaña, J. and M.A. Muriel, "Temporal self-imaging effects: Theory and application for multiplying pulse repetition rates," IEEE J. Sel. Topics Quantum Electron., 7, 728-744 (2001).
3. Azaña, J. and L.R. Chen, "General temporal self-imaging phenomena," J. Opt. Soc. Amer. B, 20, 1447-1458, (2003).
4. Bennett, C.V. and B.H. Kolner, "Aberrations in temporal imaging", IEEE J. QuantumElectron., 37, 20-32, (2001).
5. Chantada, L., C.R. Fernández-Pousa and C. Gómez-Reino, "Spectral analysis of the temporal self-imaging phenomenon in fiber dispersive lines," IEEE J. Lightw. Technol., 24, 2015-2025 (2006).
6. Cuadrado-Laborde, C., P.A. Costanzo-Caso, R. Duchowicz and E. E. Sicre, "Pulse propagation analysis based on the temporal Radon-Wigner transform", Opt. Commun., 266, 32-38 (2006).
7. Hanna, M., P. Lacourt, S. Poinsot and J.M. Dudley, "Optical pulse generation using soliton-assisted time lens compression," Opt. Express, 13, 1743-1747 (2005).
8. Kolner, B.H., "Space-time duality and the theory of temporal imaging," IEEE J. QuantumElectron., 30, 1951-1963 (1994).
9. Komukai, T., T. Yamamoto and S. Kawanishi, "Optical pulse generator using phase modulator and linearly chirped fiber gratings," IEEE Photon. Tech. Letters, 17, 1746-1748 (2005).
10. Papoulis, A., "Pulse compression, fiber communications, and diffraction: a unified approach," J. Opt. Soc. Amer. A, 11, 3-13 (1994).
11. Torres-Company, V., J. Lancis,and P. Andrés, "Unified approach to describe optical pulse generation by propagation of periodically phase-modulated CW laser light," Opt. Express, 14, 3171-3180 (2006).
12. Van Howe, J. and C. Xu, "Ultrafast optical signal processing based upon space-time dualities," IEEE J. Lightw. Technol., 24, 2649-2662 (2006).

Received: October 18, 2007.
Accepted: February 26, 2008.
Recommended by Guest Editors D. Alonso, J. Figueroa, E. Paolini and J. Solsona.