A numerical study of planar detonations

J. P. Tamagno^†, S. A. Elaskar^†‡ and J. O. Garcia^†

^† Departamento de Aeronáutica, Universidad Nacional de Córdoba, Córdoba, 5000, Argentina
jtamagno@efn.uncor.edu
^‡ CONICET, Argentina. selaskar@efn.uncor.edu

Abstract — A numerical study on the buildup and propagation of planar detonation waves in H₂ + Air combustible mixtures, based on the use of unsteady Euler equations coupled with source terms to account for rates controlled chemical activity, is presented. The computer solver works with 13 chemical species and 33 different one step reactions of a H₂-O₂ - N₂ combustion mechanism. The detonation process is initiated via the energy provided by an igniter which acts as a driver of a shock tube driving through a combustible mixture a blast (or strong shock), accompanied by exothermic chemical changes. It is shown that for each equivalence ratio of the combustible mixture, the detonation can only be triggered if the igniter energy deposition equals or exceeds a computed minimum value. When the igniter energy deposition is less than this minimum, the combustion zone start to decouple from the blast front and if that energy is diminished even more, the combustion could not take place. A particular way of generating sustained overdriven detonations, is also considered.

Keywords — Unsteady Flow; Chemically Reacting Flows; Ignition; Chapman-Jouguet Detonations; Overdriven Detonations.

I. INTRODUCTION

It is well known that any explosive mixture, can in general, go through two extremes modes of combustion. One extreme is the slow laminar deflagration mode; here the flame propagates at typical velocities of the order 1 ms^-1 relative to the unburned gases and the overpressure is small. The other extreme is the detonation mode, in which the detonation wave propagates at velocities of the order of 2000 ms^-1 and with an overpressure rise across the wave of almost 20 times the initial value. The propagation of laminar deflagrations is governed by the molecular diffusion of heat and mass from the reaction zone to the unburned mixture. On the other hand, the propagation of detonations depends on the adiabatic shock compression of the unburned mixture to increase its temperature to bring autoignition. The strong exponential temperature dependence of chemical reactions rates, makes possible the rapid combustion in the detonation mode. In between the two extremes of laminar deflagration and detonation, there is an almost continuous spectrum of burning rates, however in this work, only detonations in homogeneous gaseous mixtures of H₂ and Air are considered.

The classical Chapman-Jouguet theory, seeks the unique solution of the one-dimensional conservation equations across the detonation front in which the flow behind the wave is sonic. It involves only an equilibrium thermodynamic calculation for the detonation states (i.e. the detonation velocity, pressure, temperature, and density ratios across the wave, and the equilibrium composition of the products gases). These detonation states calculated using the classical approach agree well with experimental observations. However, parameters like the initiation energy, detonability limits, the thickness of the reaction zone and the critical tube diameter, are requiring a knowledge of the structure of the wave itself, and hence the chemical reaction rates. Following Lee (1984), these parameters are referred as the dynamics detonation parameters to distinguish from the equilibrium static detonation states obtained from the Chapman-Jouguet theory.

A century after the formulation of the successful Chapman-Jouguet theory, the estimation of dynamics detonation parameters continues being mostly, based on experimental data, see Kaneshige and Shepherd (1997). In the 1960s, experiments revealed that gas-phase confined detonations are most often characterized by unsteady, three-dimensional cellular structures, which can only in an averaged sense be predicted by one-dimensional steady theories. Since then, numerical modeling has steadily advanced to predicting the flow field behind shock induced reactions (Sharpe and Quirk, 2008), nevertheless and to the degree of our knowledge, no theory has yet described how the cellular structure is formed and sustained behind unconfined waves.

To totally preserve the concept of one dimensional planar detonation, the ignition source should also be planar. Similarly, if the flow has spherical symmetry and it is wanted to preserve, then the ignition source should also have spherical symmetry. However, if inside a duct filled with combustible mixture, the detonation is started by an ignition source which provides a 3D blast, the production of a highly three-dimensional structure of interacting and reflecting longitudinal and transverse waves should be expected. The longitudinal ones, could associate with the propagating detonation, while the transverse ones propagating normal to the direction of the detonation motion, distort the wave front. This structure will last until full equilibrium between the transverse shocks is reached and the flow becomes essentially one-dimensional. This transition from a 3D start to a final 1D detonation state cannot yet, be approached with our solver.

The planar igniter required to start a planar detonation has been conceived as a region adyacent to the closed end of the detonating system (X=0.0), filled with high temperature and high pressure helium (H_e). Then, the igniter can function as the driver of a shock tube (Tamagno et al., 2003), and use its energy to drive through a combustible medium a front blast (or strong shock) accompanied by exothermic chemical changes. This setup show consistency with the main objectives of this work: 1) to determine the energy that must be used to initiate a self sustained Chapman-Jouguet planar detonation, and in case of an overdriven start it shall decay to a Chapman-Jouguet state; 2) to verify that when the igniter energy is lower than the critical value for direct initiation, the combustion zone decouples from the blast front; 3) to generate a sustainable overdriven detonation.

This numerical study of planar detonations in H₂-Air combustible mixtures, is accomplished by solving time dependent one-dimensional Euler equations with source terms. The source terms are needed to account for the finite rate chemical activity between the constituent gases. The computer code allows the incorporation of 13 chemical reacting species (N₂, O₂, H₂, NO, OH, NO₂, HNO, HO₂, H₂O, H₂O₂, N, O, H), and 33 one step corresponding reactions. The igniter helium (He) is added as an inert species. The finite-rate chemistry mechanism describing the detailed chemical kinetics of the hydrogen oxidation in air assembled by Jachimowski (1988), is adopted. The approach taken to numerically solve the non-linear systems of hyperbolic conservation laws is based on a finite-volume form of a second order Harten and Yee TVD scheme (Yee, 1989). Regarding the source terms, it shall be noted that chemically active flows contain a range of widely varying time scales which leads to stiff differential equations. Usually, the problem of stiffness may be resolved by resorting to implicit methods. However, for chemically active flow models stiffness may not be resolved by simply using implicit techniques. If the mesh is not sufficiently fine in both space and time, spurious unphysical solutions may be computed (Toro, 2009). The implicit algorithm here employed is recognized as a point implicit approach since it treats only the source terms implicitly (Wilson, 1992). Details about the system of governing equations, the chemical source terms and its implicit treatment, are given by Tamagno et al. (2010).

II. RESULTS OF THE NUMERICAL STUDY

Experimentally, it is found that for a given mixture at given initial conditions, a definite quantity of energy must be used to initiate a detonation "instantaneously". By "instantaneously" is meant that the initial blast (or strong shock wave) generated by the igniter after the rapid deposition of its energy, has decayed to a Chapman-Jouguet detonation (Lee, 1984). If the igniter energy is less than a certain value, the combustion zone progressively decouples from the front blast as it decays. Applying the numerical approach previously described to a planar starting and propagating blast, both aspects, the tendency of the initial blast wave generated by the igniter to becoming a Chapman-Jouguet phenomena or the de-coupling of the reaction zone from the blast, are intended to be simulated. In addition, a way of starting and sustaining an overdriven detonation is presented. Note that for an inviscid and adiabatic truly planar flow, the geometry which contains it becomes irrelevant.

A. The start and the propagation of a planar detonation wave

Let us consider first, a stoichiometric mixture of H₂ + Air. Figure 1 shows in coordinates time vs. distance the blast (or shock) starting by the igniter and then propagating downstream the tube as a detonation wave (DW). Here the planar igniter or ignition source is materialized by a small region of length 2.5 mm located at the closed end of the detonating system, filled with hot and high pressure helium. The temperature of the hot helium was fixed at 3900 K and the pressure is varied from 1.0 × 10⁶ up to 4.0 ×10 ⁶ (Pa), depending on the equivalence ratio (ER) of the H₂ + Air combustible medium used. To only study the decay of a non supported overdriven detonaton wave, the length of the igniter is increased to 0.02 m and the pressure lowered to 0.7 × 10⁶ (Pa).

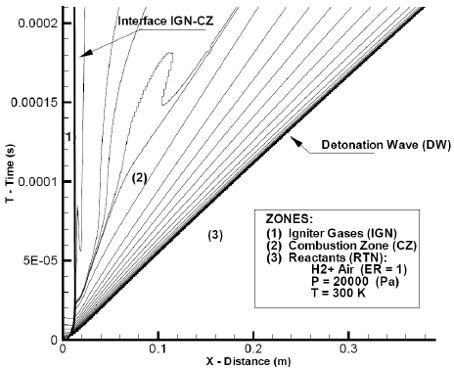
Fig. 1: Computed X-T diagram of the logarithm of constant density contours -Ign. Pres.: 1.5 × 10⁶ (Pa).

The number of cells used in 0.40 m of field length was 1600 and the time steps varied from 520000 to 720000. This large number of cells and the high number of time steps needed to obtain what are believed physical meaningful answers, are consistent with Toro (2009) statement that in chemical reacting flows not always the problem of stiffness may be resolved by simply applying implicit techniques Indeed, to achieve convergence applying the implicit algorithm here used, the time step Δtt should not have a value greater than 10^-9 s. This strong time step restriction is a consequence of the wide range of times scales involved in the finite rate chemical process considered. Keeping in mind that the width of each cell is ΔX≈ 0.00025 m, and the velocities are of the order of 1000 ms^-1, then, the only way to get the wanted increment of time is making CFL≈ 0.004.

In Figs. 2 and 3 are presented pressure and temperature as function of distance after 0.21 milliseconds of flow time. The pressure as expected, behaves like a Taylor expansion wave, showing a peak at the location of the DW and a minimum value as it approaches the closed end of the detonating system (X =0.0). The temperature behavior, describes the jump across the DW due to heat release by exothermic chemical reactions, as well as the interface that separates combustion products from igniter gases. The corresponding O₂ depletion and the H₂O formation are shown in Fig. 4.

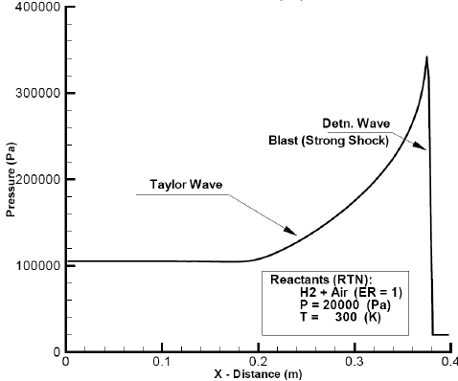
Fig. 2: Computed, pressure as function of distance at flow time=2.1 × 10^-4 (s) -Ign. Press: 1.5× 10⁶ (Pa).

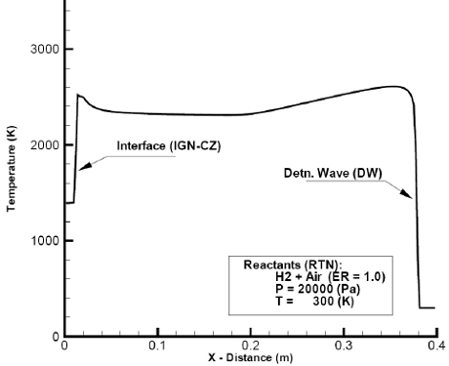
Fig. 3: Computed, temperature as function of distance at flow time=2.1 × 10^-4(s) -Ign. Press: 1.5× 10⁶(Pa).

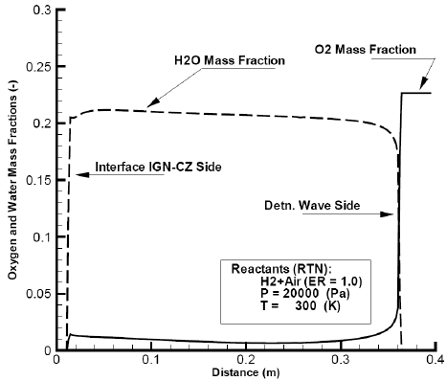
Fig. 4: Computed, oxygen and water mass fractions as function of distance at flow time=2.1×10^-4 -Ign. Press: 1.5×10⁶ (Pa).

The results up to now presented, are applicable to the H₂ + Air stoichiometric mixture (ER =1.0). Also, identical calculations with this combustible mixture at ER =0.5 and ER =2.0, were made. Of particular interest is the comparison between detonation velocities computed using Chapman-Jouguet equilibrium calculations (Gordon and McBride, 1971; Gordon and McBride, 2005; Scarpin, 2006), and using finite rate chemistry. It can be concluded from Fig. 5, that the equilibrium and finite rate calculated velocities of DW s agree satisfactorily.

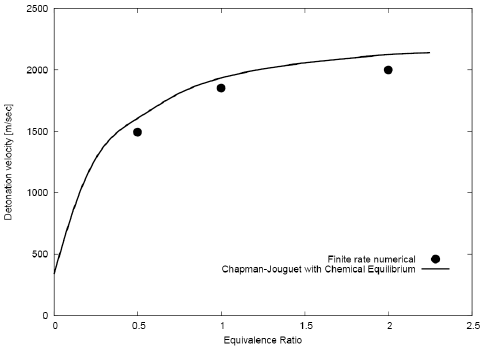
Fig. 5: Comparison between detonation velocities computed using Chapman-Jouguet equilibrium and finite rates

B. The decoupling of the reaction zone from the blast

Calculations for the stoichiometric H₂+Air mixture have shown that to produce a Chapman-Jouguet detonation wave, the igniter energy deposition shall not be less than 3000 Joules/m². If this energy deposition does not reach the minimum value, then, the combustion zone should decouple from the initial blast. To verify this statement, the igniter energy is reduced to 2800 Joules/m² and the computer program is run. Fig. 6 shows, in coordinates time vs. distance, the results obtained.

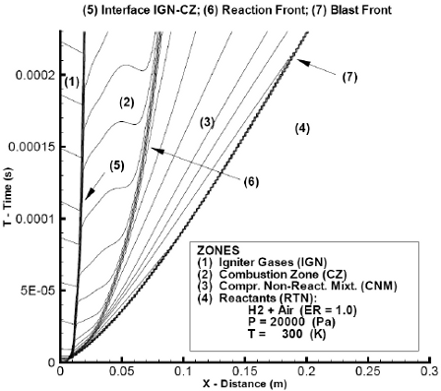
Fig. 6: Computed, X-T diagram showing the combustion zone decoupled from leading blast -Ign. Press.: 1.13×10⁶ (Pa).

After the blast (7), a non reacting compressed region (3) develops. Although the pressure in this region (see Fig. 7), peaks also immediately after the shock and progressively diminish toward the closed end, it shall be noted that the ratios pressure / reactants pressure at its peak and elsewhere in region (3), are smaller than the corresponding ratios obtained with a detonating stoichiometric H₂ + Air mixture (by a factor of 5.3 at the peak and of 3.4 at the closed and). A computed temperature distribution as function of distance is plotted in Fig. 8. A sort of reaction front (6), separating the combustion zone (2) from the zone (3), can be detected. In addition, the interface igniter-combustion zone is positioned. Figure 9 shows computed mass fractions of oxigen and water vapor.

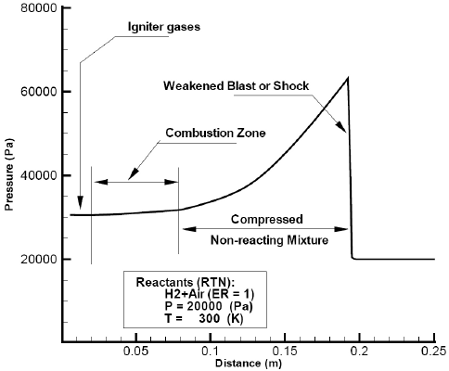
Fig. 7: Computed, pressure as function of distance at flow time=2.2×10^-4 (s) -Combustion zone decoupled from leading blast.

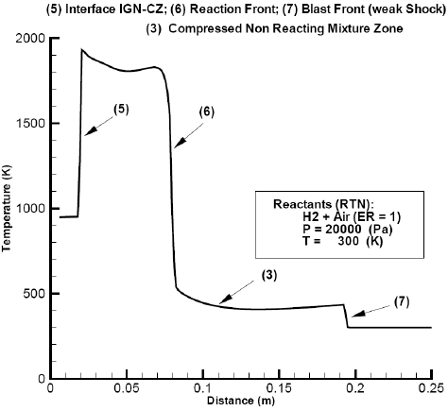
Fig. 8: Computed, temperature as function of distance at flow time=2.2 ×10^-4 (s) -Combustion zone de-coupled from leading blast.

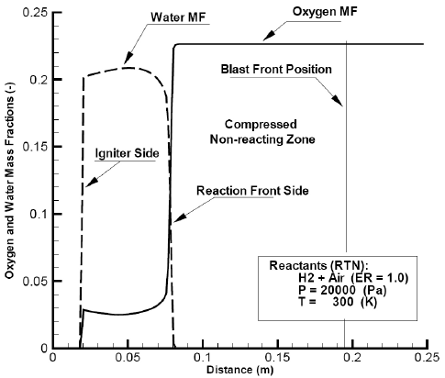
Fig. 9: Computed, oxygen and water mass fractions as function of distance at flow time=2.2×10^-4 (s) -Combustion zone decoupled from leading blast.

C. The decay of an overdriven detonation to a Chapman-Jouguet state.

The results presented in Fig. 10 show that an overdriven detonation without suitable support, it shall decay to a Chapman-Jouguet detonation state. To generate the velocity data of Fig. 10, a stoichiometric combustible H₂ + Air mixture is detonated by an igniter 0.02 m long (that is, 8 times longer than the one previously used), its pressure is 0.7×10⁶ (Pa) and its temperature is maintained at 3900 (K). It can be seen that after a short distance (0.04 m) from the igniter initial length, the velocity of the detonation wave jumps to a value higher than 2500 m/s, clearly denoting an overdriven start. As the DW moves away from the ignition source its velocity quickly diminishes approaching the Chapman-Jouguet computed value (about 1850 m/s).

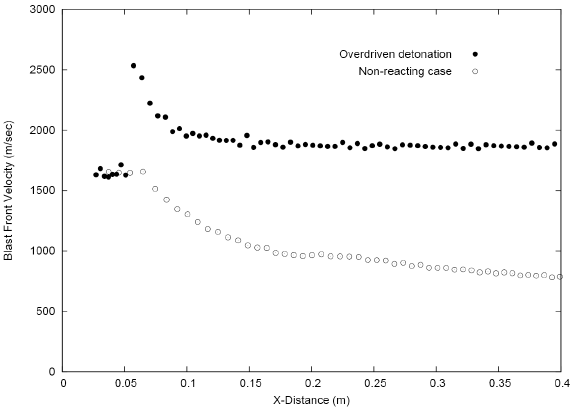
Fig. 10: Overdriven Detonation Wave decaying to a Chapman-Jouguet state -Comparison with non reacting case.

In Fig. 10, the velocity behavior of the detonating case is also compared with that of the non reacting case. This implies that the initial flow conditions are the same in both cases, but in the non-reacting no chemical activity is allowed. Notice that within the distance of 0.04 m after the igniter initial length (0.02 m), there are no mayor differences in velocity between both cases, however, as the non-reacting blast front (or shock) moves away from the ignition source, such differences end up being very significant. This is mainly due to the substantially bigger expansion which undergoes the igniter gas when not being limited by the pressure levels determined by the Taylor wave corresponding to the current detonation state.

D. Generation of an overdriven detonation

To generate a sustainable overdriven detonation traveling at a greater speed than the corresponding Chapman-Jouguet detonation, the hot and high pressure helium igniter is now assumed to be unlimited. This will guarantee the maximum support that a gaseous igniter with given thermodynamic properties, can provide. The temperature and pressure of the igniter gas are assumed to be 3900(K) and 1.0 ×10⁶ (Pa), respectively, and it will drive a hypothetical shock tube whose driven gas is a combustible H₂ + Air mixture of ER =1.0, has a pressure of 20000 (Pa) and a temperature of 300 (K). Since it is assumed that the shock tube process is non diffusive, the interface between the igniter and driven gases can be considered as a "piston" whose mass equals that of driven cells (Acosta and Tamagno, 2004). This piston, shock compress adiabatically the combustible mixture to elevate its temperature to bring autoignition. Figure 11 shows, in coordinates time vs. distance the results obtained. Figures 12 and 13, built on data taken at a flow time of 8.0 ×10^-5 (s) depict, respectively, the velocity and pressure behavior which show consistency with the interface-piston concept of driving through the combustible mixture a strong shock. The exothermic chemical change can be inferred by the depletion of oxygen and the water vapor formation (Fig. 14).

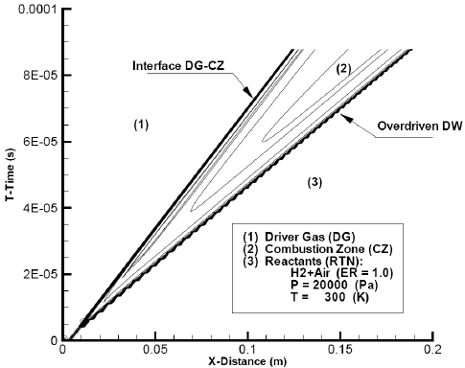
Fig. 11: Computed, X-T diagram of the logarithm of constant density contours -Overdriven detonation

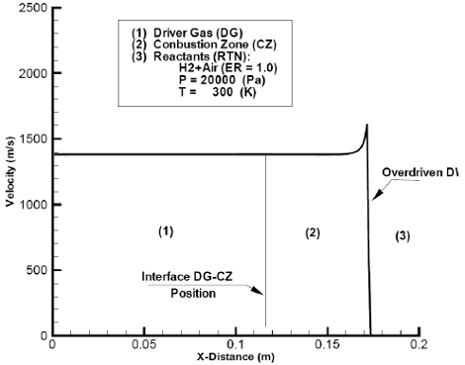
Fig. 12: Computed, velocity as function of distance at flow time=8.0×10^-5 (s) -Overdriven detonation.

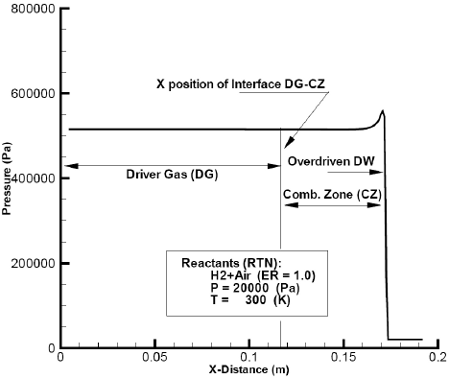
Fig. 13: Computed, pressure as function of distance at flow time=8.0×10^-5 (s) -Overdriven detonation.

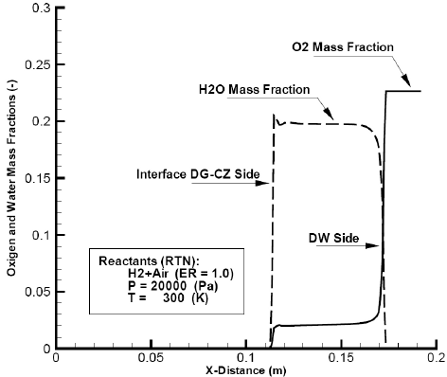
Fig. 14: Computed, oxigen and water vapor mass fractions as function of distance at flow time=8.0×10^-5(s) -Overdriven detonation.

The overdriven detonation here described, propagates at a velocity of 2118 m/s and the Chapman-Jouguet detonations previously described in subsection [II.A and II.C], makes it at 1850 m/s (see Figs. 5 and 10). The relative Mach number behind the detonation no longer approaches the sonic value as it does in the Chapman-Jouguet case, instead, it remains definitively subsonic.

III. CONCLUSION

A numerical study concerning the start and the propagation of planar detonation waves has been carried out. The numerical formulation solves the appropriate, unsteady Euler equations coupled with source terms to account for finite rates chemistry. 13 species and 33 one step chemical reactions of a H₂-O₂-N₂ combustion mechanism are considered. To totally preserve the concept of planar flow including the ignition source, this source or igniter is conceived as a driver of a shock tube that will adiabatically compress unburned combustible mixtures of H₂+Air raising its temperature beyond autoignition. Once started, the detonation becomes self sustained and can travel large distances, unless limited by unaware causes to the flow, e.g. computing time. With the exception of the overdriven case, in all others, the interface igniter-combustion zone always has remained confined within a small region (of few centimeters downstream of its initial position).

The accomplished main objectives are:

1. Quantification of the minimum igniter energy deposition required to initiate, either in lean (ER=0.5), stoichiometric (ER=1.0) or reach (ER=2.0) combustible H₂ + Air mixtures, a self sustained planar Chapman-Jouguet detonation. When the overdriven start of a detonation is not supported, it is proved that it always decay to a Chapman-Jouguet state. When this happen, the igniter pressure has dropped from its initial maximum value to the minimum one that gives the Taylor wave corresponding to this state. Furthermore, this pressure equalization limits the expansion of the gaseous igniter and fixes the position of the interface igniter-combustion zone.
2. Verification, that when the igniter energy is smaller than the minimum amount needed for direct initiation of the detonation, the combustion zone decouples from the blast front. A non reacting compressed region develops immediately behind a weakened blast and thereafter, a combustion region is positioned. Then, a sort of reaction front and its associated temperature jump can be detected at the interface between these two regions.
3. Production of a sustainable overdriven detonation wave after adapting the planar igniter used in [1] and [2] to support it, and considering the interface as a piston that shock compress the combustible mixture to induce exothermic chemical changes.

ACKNOWLEDGEMENTS
The authors would like to acknowledge and thank the support of the SECyT of the Universidad Nacional de Córdoba, CONICET and MinCyT of Provincia de Córdoba.

REFERENCES
1. Acosta, M. and J. Tamagno, "Modelado cuasi unidimensional del movimiento de un pistón en el interior de un tubo," Mecánica Computacional, 23 (2004).
2. Gordon, S. and B. McBride, "Computer program for calculation of complex chemical equilibrium composition (chapmanjouguet detonations)," NASA, SP-273 (1971).
3. Gordon, S. and B. McBride, "Cea 2.," http://www.grc.nasa.gov/CEAWeb/ ceaRequestForm.htm (2005).
4. Jachimowski, C., "An analytical study of the hydrogen-air reaction mechanism with application to scramjet combustion," NASA, Technical Paper 2791 (1988).
5. Kaneshige, M. and J.E. Shepherd, "Detonation data base," GALCIT, Technical Report FM97-8 (1997).
6. Lee, J.H.S., "Dynamics parameters of gaseous detonations," Ann. Rev. Fluid Mech., 16, 311-336 (1984).
7. Scarpin, G., Cálculo de las propiedades de mezclas de gases en equilibrio termodinámico, Maestría en Cs. de la Ing., mención Aeroespacial (UNC-IUA), (2006).
8. Sharpe, G.J. and J.J. Quirk, "Non linear cellular dynamics of the idealized detonation model: Regular cells," Combustion Theory and Modelling, 12, 1-21 (2008).
9. Tamagno, J., S. Elaskar and G. Ríos, "Numerical simulation of time-dependent reacting flows in pulse facilities," Applied Numerical Mathematics, 47, 515-530 (2003).
10. Tamagno, J., S. Elaskar and J. García, "Numerical simulation of detonation waves," MECOM (2010).
11. Toro, E., Riemann Solvers and Numerical Methods for Fluid Dynamics, Third Ed. Springer Dordrecht, Heidelberg, London, New York (2009).
12. Wilson, G., Computation of unsteady shock-induced combustion over hypervelocity blunt bodies, Stanford University, Stanford, CA, USA (1992).
13. Yee, H.,"A class of high-resolution explicit and implicit shock capturing methods," NASA, Technical Memo 101088 (1989)

Received: September 23, 2010.
Accepted: March 30, 2011.
Recommended by Subject Editor Alberto Cuitiño.