Intereses capitalización y anatocismo

Gustavo Sergio Biondo

Contador Público. Ayudante de la cátedra Matemática Financiera de la carrera de Contador Público. Universidad Nacioanal del Sur.

PRESENTACIÓN DEL CASO

Antecedentes:

El trabajo que se presenta tiene como base un caso real.

Todo se inicia a partir de la contratación de mis servicios profesionales por un Estudio Jurídico para que dictamine sobre los argumentos a utilizar en una expresión de agravios ante la Cámara de Apelaciones, en la debe sostener que la capitalización de intereses en la liquidación practicada y no aprobada en Primera Instancia, no afecta la norma del art. 623¹ del Código Civil que prohíbe el anatocismo.

En el caso, el Juez en Primera Instancia desoyó el planteo del acreedor y aceptó el del deudor, resolviendo que resultaba aplicable el procedimiento aritmético denominado "Interés Simple".

Hasta aquí es una simple demostración teórica, luego: el caso no presenta problemas.

Pero se presenta otra cuestión y es de fondo: se debe tener especial cuidado en demostrar a los Sres. Jueces de la Excelentísima Cámara de Apelaciones que si se procediera a capitalizar subperiódicamente los intereses no se estaría cometiendo un delito.

Si así no fuere las posibilidades de éxito del reclamo serían prácticamente nulas.

En particular

Concretamente es un caso donde una empresa constructora tiene pendiente de cobro un saldo de dinero por obras realizadas.

En el contrato de locación de servicios se había pactado como tasa de interés compensatoria por mora "a la tasa anual de interés que cobra el Banco de la Provincia de Buenos Aires para descuentos de certificados de obras públicas".

Para tal operatoria y en tal sentido el Banco de la Provincia de Buenos Aires publica una "Tasa nominal anual vencida para operaciones a 30 días" la cual, obviamente, varía periódicamente sin razón alguna de variabilidad.

Liquidaciones

El acreedor liquida el interés compensatorio de la siguiente manera: toma como capital la suma adeudada – que la mantiene siempre en ese mismo valor – y lo multiplica por el tiempo en el que se mantiene la tasa y luego por esta; y así sucesivamente va agregando factores a medida que cambian las tasas hasta el día de efectivo pago.

Evidentemente el error radica en que la tasa de interés a utilizar por el lapso total debe ser la que efectivamente resulte de la subperiódica capitalización de cada una de las tasas vigentes durante todo el período de duración de la deuda.

Dicho en otras palabras: el interés a pagar / cobrar será el obtenido por la aplicación de la tasa efectiva resultante de las correspondientes proporcionalizaciones y consecuentes capitalizaciones de todo el período.

Conclusión

Luego y en el marco de lo antes dicho es que, con las modificaciones que corresponden al cambio del ámbito de presentación, lo he desarrollado para presentarlo ante el Departamento de Ciencias de la Administración de la Universidad Nacional del Sur.-

MARCO TEORICO

Consideraciones previas:

Por sentido común puede afirmarse que no es lo mismo disponer de una cosa hoy que en otro momento del tiempo, y por el mismo sentido común se concluye que debe compensarse esa carencia.

Esa compensación puede acordarse de cualquier manera, sea de la misma o diferente especie que la cosa en cuestión.

Cuando la cosa es de absoluta liquidez y la compensación se pacta en la misma especie, o sea dinero, la retribución es agregando o quitando al capital inicial una suma que se llama interés.

Luego y por el mismo sentido común puede definirse al interés como la diferencia del valor de un capital entre dos diferentes momentos del tiempo.

Luego puede concluirse que es condición necesaria para la generación de intereses que:

1. debe transcurrir el tiempo
2. la compensación sea en la misma especie de la cual se parte.

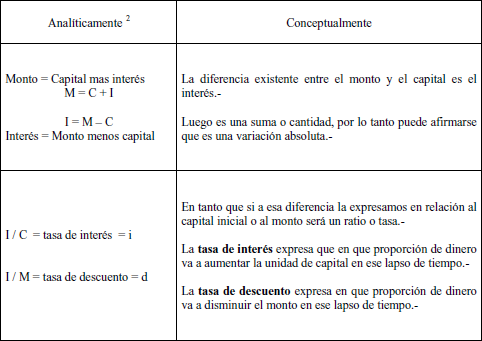
Esa diferencia siempre será expresada como una cantidad de dinero, pero independientemente de la forma que se le dé siempre podrá ser expresada como una proporción – ratio, tasa o porcentaje - del capital inicial.

Esa compensación en dinero es una variación absoluta en tanto que expresado como proporción es una variación relativa.

Son dos ópticas distintas y complementarias de un mismo problema.

Variaciones absolutas y variaciones relativas

Por lo hasta ahora visto se puede afirmar que según el tipo de análisis o fin que se persiga la variación o diferencia entre dos cantidades será posible plantearla o evaluarla - indistintamente - de dos maneras diferentes: absolutas o relativas.

Como dato o premisas partimos de que una variación absoluta es una cantidad de la misma especie de la que se esta tratando en tanto que una variación relativa es un número que expresa la relación - ratio o tasa - de variabilidad de las magnitudes en cuestión.

Estas dos maneras son formas distintas de presentar o plantear un mismo problema, es mas son complementarias.

Cuando se trate de dinero serán tasas de Interés, donde:

Independientemente de la forma en que se acuerde es necesario y conveniente tener presente que para un análisis de flujos deben considerarse las variaciones absolutas en tanto que si el análisis fuera de rentabilidad deben utilizarse las variaciones relativas.

Tiempo: periodos y subperíodos

El lapso o plazo total de duración de la operación puede ser de uno o mas períodos.

A su vez cada período puede ser subdividido en partes o "subperíodos" de tiempo, estos pueden ser tantos como las partes acuerden.

Tasa

Respecto a esta variable debe tenerse presente que no necesariamente la tasa debe estar expresada en la misma magnitud que el tiempo.

En caso que no lo estuvieren debe, previo al cálculo de intereses, sincronizarse ( adecuarse o compatibilizarse ) el tiempo con la tasa.

Sincronización

Si el tiempo y la tasa están expresados en magnitudes diferentes es necesario compatibilizarlos - sincronizarlos - para recién luego proceder al cálculo del interés.

De otra manera el resultado obtenido va a ser un número que no va a representar la diferencia del valor de ese capital en el tiempo.

Ello es así pues de proceder de una manera distinta se estaría operando con variables que no son compatibles.

A manera de ejemplo se puede afirmar que si la tasa esta expresada en una magnitud anual y el tiempo en días, si – previamente - no convertimos la tasa anual a una tasa diaria el resultado obtenido será es el interés de ese capital para períodos anuales y no diarios.

Capitalización

Para poder avanzar en el concepto de interés efectivo o rendimiento real es necesario tener en claro el concepto de capitalización.

Capitalizar: es adicionar al capital inicial del período/subperiodo la suma de dinero que en concepto de intereses se han generado en el mismo. Esa suma resultante ( C + i ) pasa así a conformar el capital inicial del siguiente.

Evidente es que utilizando este procedimiento el resultado obtenido va a ser mayor que el que resultaría de aplicar la tasa nominal periódica sin ningún tipo de capitalización en el tiempo considerado.

Esa diferencia van a ser los intereses ganados por los mismos intereses y es por este procedimiento que se genera lo que se le llama anatocismo.

Equivalencia financiera

Por todo lo antes visto puede aseverarse que se debe tener como premisa que toda evaluación y análisis financiero debe ser realizado bajo el régimen de "capitalización compuesta" obteniéndose así resultados efectivos que permitan determinar la real "equivalencia financiera" y que por otra parte no necesariamente las tasas de interés a utilizar estarán expresadas en la magnitud del análisis y/o en la de los períodos y/o subperíodos que se consideren.

Puede concluirse que para todo análisis debe previamente determinarse la tasa de interés a utilizar moviéndose dentro del eje del tiempo con tasas equivalentes entre si.

El concepto de equivalencia respecto a las tasas hace que determinado un periodo - cualquiera que este sea - el razonamiento siempre será el mismo, luego al momento del análisis la "formula" a utilizar será siempre la misma.

Ello es así pues el concepto del cual se parte es el mismo, por lo tanto es la "equivalencia" el concepto matriz, general y básico en tanto que la "efectividad" de una tasa es una caso particular de expresar esa equivalencia.

Tasas equivalentes y/o efectivas

Si definimos a "m" como al exponente de la fórmula a utilizar para la determinación de tasas equivalentes y efectivas - por usos y costumbres – cuando "m" mayor que uno al resultado obtenido le llamamos "tasas efectivas" y cuando "m" es menor que uno al resultado le llamamos "tasas equivalentes".

Presentación de la fórmula: potencias y/o raíces

Debe tenerse presente que en toda potencia el exponente puede ser un número entero o fraccionario y a su vez positivo o negativo.

Por tratarse de rendimientos y equivalencias solo utilizaremos los exponentes positivos mayores, menores o iguales a uno, enteros o fraccionarios.

Por otra parte las potencias pueden expresarse como tales o bien como raíces o combinación de ambas.

Si el número es entero y mayor que uno la forma usual es a^b en tanto que si el exponente es menor que uno y no periódico usualmente se expresa como una raíz 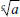y si así no fuere como una combinación de potencia y raíz .

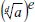Ejemplos: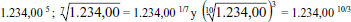

CUESTIONES PRÁCTICAS:

Formas de plantear la tasa de interés

Antes de iniciar el cálculo del interés debe tenerse presente la forma en que está planteada la tasa pues puede estar en uno de los dos siguientes tipos:

Tasa periódica
Tasa subperiódica

A su vez si es periódica puede ser:

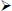Tasa nominal
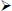Tasa efectiva

En tanto que si es subperiódica puede ser:

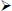Tasa proporcional
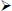Tasa equivalente

Tasa periódica o tasa subperiódica?

Generalmente la tasa que informan las entidades financieras para operaciones de descuento es una tasa anual, en tanto que los descuentos de pagarés o documentos similares no necesariamente son por lapsos iguales a un año, pueden se menores o mayores.

Por lo tanto debe, necesariamente, adecuarse la tasa al período en cuestión.

Este procedimiento puede ser de dos maneras distintas según se trate de una tasa nominal o una tasa efectiva para ese período anual.

Si la tasa es nominal debe determinarse una tasa proporcional en tanto que si es una tasa efectiva corresponde hallar una tasa equivalente.

Tasa periódica: nominal o efectiva – Tasa subperiódica: proporcional o equivalente ?

Por lo ya visto si la tasa planteada para el período es una tasa nominal debe – primeramente - proporcionalizarse al subperiodo, en tanto que si es una tasa efectiva el procedimiento es otro y consiste en determinar una tasa equivalente.

Luego de la aplicación de una tasa nominal anual debidamente proporcionalizada resultaran intereses superiores a los que se hubieran generado de la aplicación de esa tasa nominal sin subperíodos de capitalización.

Evidente es que el interés será cada vez mayor cuanto mas subperíodos de capitalización existan dentro del período.

Por ejemplo si la tasa es nominal anual y la capitalización mensual va a dar como resultado una suma de intereses mayor que si la capitalización fuera semestral.

En ninguno de los dos casos puede decirse que el resultado sea el no acordado entre las partes y por supuesto que en ambos casos existe generación de intereses sobre intereses ya generados.

Otra cosa muy distinta es fijar una tasa efectiva para el período, en tal caso se esta diciendo que el resultado o interés total generado para ese lapso debe ser el mismo que resulte de la aplicación de esa tasa para ese plazo si no existieran subperíodos de capitalización.

Luego debe encontrarse una tasa tal que capitalizada en cada uno de los subperíodos considerados de cómo resultado el mismo que se hubiera obtenido si no existieren subperíodos de capitalización dentro del período y el tiempo o plazo de la operación hubiera sido igual a la magnitud en que esta expresada la tasa.

Evidente es que mayor será la tasa de variabilidad cuanto mayor sea el período considerado, lo que no quiere decir que haya variado mas o menos, es lo mismo pero da lugar a una "ilusión numeraria" pues la realidad económico financiera es una sola mas allá del período en consideración.

Por ejemplo:

Si la tasa efectiva anual es del 25 %, el plazo de un año y el régimen de capitalización es trimestral, la tasa a aplicar para cada uno de esos subperíodos debe dar como resultado a consecuencia de su capitalización el 25 % anual. Decimos que estamos utilizando una tasa subperiódica equivalente.

En tanto que si fuera el 25 % nominal anual, el plazo de un año y el régimen de capitalización trimestral, la tasa a aplicar para cada uno de esos subperíodos dará como resultado un interés superior al 25 % para ese año. Decimos que estamos utilizando una tasa subperiódica proporcional .

"Tasa nominal o cotizada. Esta es la tasa que cotizan los prestamistas y prestatarios. Los profesionales del mercado de acciones, bonos, hipotecas, préstamos comerciales, préstamos al consumidor, banca y otros sectores más expresan todos los contratos financieros en términos de tasas nominales. Por lo tanto si se habla acerca de las tasas con que un banquero, un corredor, un prestamista de hipotecas, una compañía de financiamiento de automóviles o un funcionario de préstamos para estudiantes, por lo general se referirán a las tasas nominales. Sin embargo para que tenga significado, la cotización de la tasa nominal también debe incluir el número de periodos de composición por año". J. Fred Weston y Eugene F. Brigham, (1993) -

VARIACIONES EN EL TIEMPO

Para entender claramente el concepto "anatocismo" debe plantearse el análisis a la luz de todo lo antes visto respecto a tasas, tiempo y regímenes de capitalización.

De ese concepto - capitalización – resulta que el interés es una función exponencial y esa forma de aumentar no es patrimonio exclusivo del dinero.

Todo lo contrario es un procedimiento común a todo proceso de crecimiento, a manera de ejemplo:

La variación ( crecimiento ) poblacional si bien se expresa en forma anual no lo hace en ese período sino que varía - día a día, hora a hora, minuto a minuto, etc. - sobre la cantidad de personas existentes al final de cada uno de ellos y no en "saltos" anuales. Se puede asimilar el período al lapso anual y los subperíodos a la forma en que dividimos ese lapso.
El costo de la vida, que mensualmente se registra, no es la variación que en forma espontánea se da el último día del mes respecto a los precios del primer día. Es la variación que día a día van teniendo los precios y que por una cuestión convencional se expresan en forma mensual.
Si un litro de aceite cuesta $ 10,00 el día 01 de marzo y $ 17,00 el día 31 de marzo, en el período considerado ha variado en un 70 % en tanto que si lo subdividimos en subperíodos diarios ha variado 1,7845 % diario. El 70% mensual no es mas que el 1,7845 % diario, ambas tasas en términos relativos expresan lo mismo solo que numéricamente difieren pues están expresadas en magnitudes de tiempo diferentes.

Ello es así pues las variaciones siempre se suceden sobre el valor inmediato anterior y no sobre cualquiera otro del pasado.

Con el interés ocurre lo mismo: debe calcularse sobre el importe del período inmediato anterior, suma que ya contiene los intereses generados en el tiempo transcurrido.

Por supuesto que es posible determinar una variación para un lapso menor (subperiodo), sea este semanal, quincenal, diario, etc.

En tal caso debe tenerse presente que esa variación deberá considerar que los valores se alteran dentro del período sobre el valor final del subperiodo inmediato anterior, el cual – por supuesto - ya contiene el aumento correspondiente al día o período inmediato anterior y por lo tanto no será – matemáticamente - una cuestión lineal sino exponencial.

Luego la tasa de interés – expresada usualmente en tanto por ciento - es un ratio que indica en que parte porcentual va a variar cada unidad de capital en cada unidad de tiempo.

A medida que se modifique esa unidad de tiempo se alterará el valor de la tasa lo que hará que se altere la variación absoluta de ese capital; pero el interés, medido en valores relativos, va a ser siempre el mismo.

Es así como funcionan las finanzas, la economía y la vida en general, por lo tanto debe tenerse presente esta realidad para un racional y exacto análisis.

CONCLUSIÓN:

Por anatocismo se entiende el cálculo de intereses sobre el capital inicial mas los intereses generados hasta el período inmediato anterior.

En este caso se puede afirmar que "anatocismo" y "capitalización" son sinónimos.

El sistema financiero en su totalidad funciona en base al movimiento exponencial, luego el tratar de impedir que los valores varíen sobre su magnitud inmediata anterior es una clara demostración de desconocimiento del funcionamiento de las finanzas, es una decisión teórica de impracticable aplicación práctica.

Concretamente en esa decisión subyace un error de fondo de tal magnitud que la torna inválida pues el anatocismo siempre existe y la confusión surge a consecuencia de no tener en claro que una variación relativa no es lo mismo que una variación absoluta.

Sin duda alguna que el espíritu o intención – al considerar ilegal el anatocismo - es la defensa del deudor y tender a el bien común, pero evidentemente que no es esa la manera o forma de hacerlo.

En la búsqueda del mismo fin - otra cosa muy distinta - es fijar parámetros para el manejo o aplicación de tasas de interés por ser abusivas, expropiatorias y/o impagables o el tratar de evitar que por dolosos manejos en la publicación o utilización de esas tasas se contribuya al engaño.

Un claro ejemplo de esto se daba cuando en las pizarras de las entidades financieras se publicaban las tasas nominales, ellas – por efecto de la capitalización - no reflejaban en absoluto el rendimiento o costos real que esas mismas tasas nominales generan.

Claro ejemplo de lo antes dicho es que hoy por disposición del Banco Central de la República Argentina se deben publicar las tasas efectivas. Ella es una clara decisión que ratifica que para el análisis financiero y/o cálculo de intereses deben utilizarse procedimientos de capitalización, acumulativos o exponenciales y no los lineales resultantes de la aplicación de tasas nominales.

ANEXO I - Tasa de descuento y tasa de interés

Monto = Capital + Interés
Interés = Monto – Capital

Monto = C ( 1 + i ) ⁿ
Interes = C ( ( 1 + i ) ⁿ – 1 )

Una alternativa

Tasa de descuento

d = ( M – C ) / M =
= ( C ( 1 + i ) ⁿ – C ) / C ( 1 + i ) ⁿ
= ( ( C ( 1 + i ) ⁿ ) / C ( 1 + i ) ⁿ ) / ( C / C ( 1 + i ) ⁿ ) =
= 1 – ( 1 / ( 1 + i ) ⁿ ) =

Para la unidad de tiempo: n = 1

= ( 1 + i – 1 ) / ( 1 + i ) =
= i / ( 1 + i ) =
d = i / ( 1 + i )

Tasa de interés

i = ( M – C ) / C =
= ( C + I – C ) / C =
= I / C = i
Luego
i = d / ( 1 – d )

Otra manera:

Partiendo de la base que el valor final de una operación es igual a su valor actual multiplicado por un factor de capitalización, es decir:

V_n = V_o ( 1+ i )

Luego:

V₀ = V_n / (1+ i )
Si V_n = 1
V₀ = 1 / (1+ i ) (a)
Por otra parte:
V₀ = V_n – d
V₀ = 1 – d (b)
Luego de (b) y (a)
1 – d = 1 / (1+ i )
d = 1 - ( 1 / (1+ i ) )
d = ( 1 + i - 1 ) / (1+ i )
d = i / (1+ i )

Ejemplo:

Determinar el valor actual de una obligación cuyo valor nominal es de $ 500.000,00 que vence dentro de 62 dias, siendo la tasa de interés del 11 % efectivo para 30 dias.

Una manera de resolverlo:

V₀ = V_n / (1+ i ) ^m1/m2
V₀ = 500.000 / (1+ 0,11 ) ^{62 / 30}
V₀ = 500.000 _/ 1.240702
V₀ = 402.997,65

Otra forma:

a ) Tasa efectiva para 62 dias:

i = ( 1 + i ) ^m1/m2 – 1
i = (1+ 0,11 ) ^{62 / 30} - 1
i = 0,240702
b) Luego determinar la tasa de descuento:
d = i / (1+ i )
d = 0,240702 / (1+ 0,240702 )
d = 0,194004
c) Luego el Valor actual para la unidad de capital será:
V₀ = 1 – d
V₀ = 1 – 0,194004
V₀ = 0,8059952
d) Luego el Valor actual para el total será:
V₀ = 500.000,00 * 0,8059952
V₀ = 402.997,60

CASO PRACTICO

Planteo

Dada una tasa del 10 % nominal anual, determinar:
a - La tasa proporcional para 7 días -
b - La tasa proporcional para 70 días -
c - La tasa efectiva a 70 días partiendo de a) -
d - La tasa efectiva a 70 días partiendo de b) -
e - La tasa efectiva anual partiendo de c) -
f - La tasa efectiva anual partiendo de d) -
g - La tasa equivalente a 7 días partiendo de e) -
h - La tasa equivalente a 70 días partiendo de f) -
i – La tasa equivalente para un día.
j – La tasa equivalente para 7 días partiendo de i) -
k - La tasa equivalente para 70 días partiendo de i) -
l - La tasa equivalente para 365 días partiendo de i) -
m – Las tasas efectivas periódicas partiendo de j, k y l ) –

Consideraciones previas a la resolución:

Rendimientos reales

Para determinar la tasa que debe ser utilizada en el análisis financiero debe aplicarse el concepto de "rendimiento real" y sabemos que su fórmula es:

( 1 + i ) ^m – 1 = i_m

Aplicaciones:

" Una tasa es equivalente a otra cuando: en un mismo período de tiempo pero con diferentes subperíodos de capitalización las dos tienen el mismo rendimiento efectivo".

Siendo la incógnita i₁ , m₁ y m₂ positivos, mayores, iguales o menores que uno (1), enteros o fraccionarios, se puede expresar como que:

( 1 + i ₁ ) ^m₁ – 1 = ( 1 + i₂ ) ^m₂ – 1

( 1 + i ₁ ) ^m₁ = ( 1 + i₂ ) ^m₂

i ₁ = ( 1 + i₂ ) ^(m₂ ^{/ m}₁ ⁾ – 1

Por definición tanto m₂ como m₁ son fracciones que indican la cantidad e veces que esa tasa se va a capitalizar en el período, luego: se puede afirmar que tienen el mismo numerador y su denominador será la cantidad de unidades que del numerador toma.

Por lo tanto si:

m₁ = a/ b
m₂ = a / c

m₂ / m₁ = (a / c) / ( a / b)
m₂ / m₁ = b / c

Reemplazando en:

i ₁ = ( 1 + i₂ ) ^(m₂ ^{/ m}₁ ⁾ – 1
i ₁ = ( 1 + i₂ ) ^(b/c) – 1

Luego, como b es el denominador de la tasa que he tomado como incógnita y c es el denominador de la tasa que tengo como dato, puedo afirmar que la tasa equivalente que estoy buscando será igual a la raíz c de la tasa que tengo como dato mas uno, luego capitalizada b veces, todo eso menos 1.

Se puede interpretar ese resultado como que se esta reduciendo la tasa (dato) a la mínima unidad de cuenta posible, o sea la tasa equivalente unitaria, y luego se capitalizo tantas veces como sea necesario.

Ejemplo:

Dada una tasa del 5 % para períodos de 45 días determinar la tasa equivalente para operaciones a 90 días.

( 1 + i ₁ ) ^m₁ – 1 = ( 1 + i₂ ) ^m₂ – 1
i ₁ = ( 1 + i₂ ) ^m₂ ^{/ m}₁ – 1
i ₁ = ( 1 + i₂ ) ^{a/c / a/b} – 1
i ₁ = ( 1 + i₂ ) ^b/c – 1

m₁ = a/ b = 365/90
m₂ = a / c = 365/45

( 1 + i ₁ ) ^365/90 – 1 = ( 1 + 0,05 ) ^365/45 – 1
( 1 + i ₁ ) ^365/90 = ( 1 + 0,05 ) ^365/45
i ₁ = ( 1 + 0,05 ) ^{365/45 * 90/365} – 1
i ₁ = ( 1 + 0,05 ) ^90/45 – 1
i ₁ = 0,1025

Comprobación:

1 – Capitalizando ambas tasas al período anual

( 1 + 0,1025 ) ^365/90 – 1 = ( 1 + 0,05 ) ^365/45 – 1
( 1,1025 ) ^365/90 – 1 = ( 1,05 ) ^365/45 – 1
0,4854866 = 0,4854866

2 – Capitalizando la tasa del subperiodo menor al mayor.

( 1 + 0,05 ) ^90/45 – 1 = 0,1025

Resultados:

Análisis de los resultados:

■ Amplitud de los subperíodos, consecuencias:

Porqué el resultado de a) es numéricamente menor que el de b)?

Si una tasa nominal periódica permanece constante ante el aumento de dias de duración de los subperíodos, la consecuencia inmediata respecto a los subperíodos es que a medida que aumentan los días este "crece" y por lo tanto "caben" menos subperíodos dentro del período.

Luego:

1. Se suceden menos capitalizaciones dentro del período.
2. Las tasas subperiódicas ( proporcionales y equivalentes ) tienden a ser numéricamente mas grandes.
3. La tasa efectiva resultante disminuye, es decir que tiende a ser numéricamente menor.

Ello es a consecuencia de que al proporcionalizar la tasa por el mismo valor que luego se potencia el resultado tiende a disminuir a medida que aumentan los días del subperíodo.

Es lógico que así sea pues al permanecer constante el numerador y variar el denominador el resultado tiende a disminuir a medida que aumenta el valor del denominador.

■ Dada una tasa nominal periódica la tasa proporcional para un subperíodo es igual a la tasa equivalente que corresponde al rendimiento efectivo de la precitada tasa subperiódica.

Así es pues antes de la primer capitalización el rendimiento efectivo es igual a la tasa nominal divida la cantidad de subperiodos.

Si bien son numéricamente iguales conceptualmente son diferentes pues esa tasa es equivalente respecto a la tasa efectiva periódica y proporcional respecto a la nominal.

Por ello g) es igual a )

Esa tasa proporcional resulta ser también tasa efectiva para ese mismo subperíodo. Por ello b es igual a d.

■ Dada una tasa efectiva periódica determinar a partir de allí una tasa equivalente para un subperíodo u otros:

Esa tasa equivalente obtenida para ese subperíodo es también efectiva respecto a ese mismo subperíodo y equivalente para cualquiera otra que se determine a partir de la precitada efectiva periódica o bien de alguna otra resultante de capitalizar la equivalente hallada.

Luego a y c son equivalentes con e y a su vez e es el rendimiento efectivo de ambas para el período dado.

A su vez por ello es que b, d y h son iguales.

■ Dada una tasa efectiva periódica a partir de allí determinar la tasa equivalente para el menor subperíodo posible:

A partir de la tasa efectiva periódica se pueden determinar las tasas equivalentes para cualquier subperíodo que se desee. Casos i, j, k y l –

Esas tasas equivalentes subperiódicas así determinadas son también efectivas para cada uno de esos subperíodos.

En tanto que las tasas efectivas periódicas resultantes para esos subperíodos van a ser iguales. Caso m.

Notas

¹ Art. 623: No se deben intereses de los intereses, sino por obligación posterior, convenida entre deudor y acreedor, que autorice la acumulación de ellos al capital, o cuando liquidada la deuda judicialmente con los intereses, el Juez mandase pagar la suma que resultare, y el deudor fuese moroso en hacerlo.
² Se agrega como Anexo I un desarrollo al respecto

BIBLIOGRAFÍA
1. Miguel M. Tajani, (1970), Matemática Financiera, Buenos Aires, Argentina, Cesarini Hnos. Editores.
2. Rodolfo Apreda, (1984), Curso de Matemática Financiera en un contexto inflacionario, Buenos Aires, Argentina, Editorial Club de Estudio.
3. Gustavo Sergio Biondo, (1999), Valor del Dinero en el Tiempo, Bahía Blanca, Argentina, Editorial de la Universidad Nacional del Sur, Serie Extensión.
4. Pol Santandreu, (1996), Matemática Financiera, Barcelona, España,.Ediciones Gestión 2000 SA.
5. Alberto Motoyuki Yasukawa, (2000), Matemática Financiera, Córdoba, Argentina, Despeignes Editora.
6. J. Fred Weston y Eugene F. Brigham, (1993), Fundamentos de Administración Financiera, Decima edición, México DF, México, Mac Graw Hill Interamericana de México SA.
7. Richard A. Brealey, Stewart C. Myers y Alan J. Marcus, (1999), Principios de Dirección Financiera, Madrid, España, Mac Graw Hill Interamericana de España SA.
8. Anales de Jornadas Universitarias de Profesores de Matemática Financiera: XV Bahía Blanca (Buenos Aires), 1994; XVI Morón (Buenos Aires), 1995; XVII Resistencia (Chaco), 1996, XVIII Córdoba, 1997; XIX La Plata (Buenos Aires), 1998; XX Paraná (Entre Ríos), 1999; XXI Mar del Plata, 2000 y XXII Concordia ( Entre Ríos), 2001.