Funciones de utilidad y estimación de la aversión al riesgo: revisión de la literatura

Utility functions and estimation of risk aversion: literature review

Etelvina Stefani Chavez¹, Gastón Milanesi², Gabriela Pesce³

¹ Departamento de Ciencias de la Administración, Universidad Nacional del Sur. Becaria doctora del Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET). E-mail: chavez.etelvinastefani@gmail.com
² Departamento de Ciencias de la Administración, Universidad Nacional del Sur. E-mail: milanesi@uns.edu.ar
³ Departamento de Ciencias de la Administración, Universidad Nacional del Sur. E-mail: gabriela.pesce@uns.edu.ar

Fecha de recepción: 15/5/2017
Fecha de aceptación: 12/9/2017

Resumen
El trabajo presenta un compendio no exhaustivo de los antecedentes teóricos sobre la utilidad de los individuos y una sistematización analítica de diferentes propuestas de formas funcionales que esta puede adoptar. Se presentan la función de utilidad con aversión al riesgo absoluta constante (CARA), la función con aversión al riesgo relativa constante (CRRA), la función con aversión al riesgo absoluta hiperbólica (HARA), la función Expo-Power (EP), la función de aversión al riesgo de potencia (PRA) y la función de tres parámetros flexibles (FTP). Para cada una de ellas se detallan las características intrínsecas en cuanto a las preferencias de los individuos, teniendo en cuenta los coeficientes de aversión absoluta y relativa al riesgo. Finalmente, se realiza un análisis de sensibilidad de la utilidad y los coeficientes de aversión al riesgo frente a cambios en el nivel de riqueza, mostrando cómo se comportan las diferentes funciones.

Palabras clave: Utilidad; Aversión al Riesgo Absoluta y Relativa; Forma Funcional; Preferencias Ante el Riesgo; Elección en Condiciones de Incertidumbre.

Abstract
This paper presents an undetailed summary of the theoretical background on the utility of individuals and an analytical systematization of the different functional forms of the utility function. The constant absolute risk aversion (CARA) utility function, the constant relative risk aversion (CRRA) function, the hyperbolic absolute risk aversion function (HARA), the Expo-Power function (EP), the power risk aversion function (PRA) and the flexible three parameter function (FTP) are described. For each function, the intrinsic characteristics of the preferences of individuals are listed, taking into account the absolute and relative risk aversion coefficients. Finally, a sensitivity analysis of utility and risk aversion coefficients against changes in the level of wealth is made, showing how the different functions behave.

Keywords: Utility; Absolute and Relative Risk Aversion; Functional Form; Risk Preferences; Choice Under Uncertainty.

JEL: D810.

1. Introducción

A través de los años se han propuesto innumerables funciones de utilidad, buscando obtener una forma funcional simple y flexible que permita representar una variedad de preferencias frente al riesgo. De todas maneras, es generalmente aceptado que la función debe ser creciente respecto de la riqueza, esto es, se prefiere más a menos, y que debe ser cóncava, reflejando la aversión al riesgo que exhiben los individuos, lo que también se encuentra ampliamente demostrado en la literatura académica. Además, otras características deseadas son: (1) que presente aversión al riesgo absoluta decreciente (DARA) ante aumentos de la riqueza, ya que se supone que a medida que se incrementa la riqueza de un individuo menor será su aversión al riesgo; y (2) aversión al riesgo relativa constante (CRRA), lo que implica que las decisiones óptimas son invariables ante cambios en la escala de riqueza (Saha, Shumway, & Talpaz 1994).

En el presente trabajo se pretende hacer un relevamiento no exhaustivo de las diferentes funciones de utilidad encontradas en la literatura, describiendo sus principales características y su uso en la estimación empírica de coeficientes de aversión al riesgo. Metodológicamente, se lleva a cabo una revisión documental de textos clásicos y contemporáneos, dado que se trata de un estudio teórico del estado del arte en la temática a abordar.

La siguiente sección presenta algunos antecedentes teóricos del tema. La sección 3 describe las funciones de utilidad consideradas en este trabajo. El apartado 4 contiene un análisis de sensibilidad de las funciones presentadas en la sección anterior, para estudiar el comportamiento de la utilidad con respecto al nivel de riqueza. También, se realiza una comparación de la aversión al riesgo, tanto relativa como absoluta, que presentan las funciones de utilidad estudiadas para distintos niveles de riqueza. Finalmente, se presentan las consideraciones finales en la parte 5.

2. Antecedentes teóricos

El desarrollo de las funciones de utilidad se enmarca dentro de lo que se conoce como teoría de la elección en condiciones de incertidumbre. En este sentido, Bernoulli (1738) fue el primero en plantear que se decide a partir de la utilidad y no del valor esperado o del precio y que esa utilidad tiene una función de tipo logarítmica, es decir que la utilidad marginal es decreciente, llegando a un punto donde una unidad más de riqueza no aporta más utilidad.

Muchos años después, von Neumann y Morgenstern (1944) desarrollan la Teoría de la Utilidad Esperada, en la cual no presentan una forma funcional de utilidad, sino que establecen la forma de calcular la utilidad esperada de un conjunto de alternativas de elección planteadas en forma de loterías, cuyo cálculo sería el de la ecuación 1.

Ecuación 1

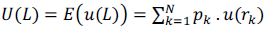Siendo U(L) la utilidad esperada de la lotería, que se calcula como la esperanza matemática de las utilidades de los resultados de las alternativas; p la probabilidad de ocurrencia de cada escenario, r su resultado correspondiente; y u(r_k) la utilidad del resultado de la alternativa k.

En teoría, se podría definir la función de utilidad de un individuo por extrapolación de las utilidades que expresa en cada alternativa de elección de diversas loterías (Cárcamo, 2016), así como también considerando los axiomas de la función que plantean los autores.

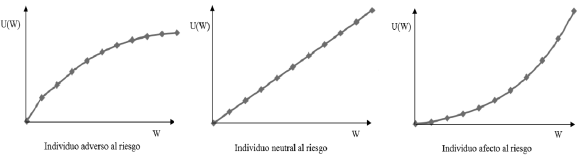
A su vez, estos autores definen los comportamientos frente al riesgo, a partir de la comparación de la utilidad derivada del resultado esperado de una lotería, comparada con la utilidad derivada del equivalente de certeza de esa lotería. De esta manera, si la primera utilidad mencionada es menor a la segunda, el agente es adverso al riesgo, si es igual es neutral y si es mayor es afecto o propenso al riesgo. Así, las personas adversas al riesgo tendrían una función de utilidad cóncava, las afectas convexa y las neutrales lineal. Estos tres comportamientos se pueden apreciar en la ilustración 1.

Ilustración 1 Función de utilidad de von Neumann y Morgenstern (1944)

Fuente: elaboración propia.

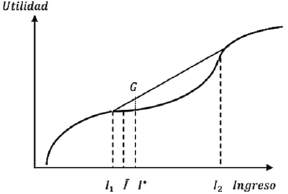
Posteriormente, Friedman y Savage (1948) proponen una función de utilidad según la cual, para ciertos niveles de riqueza, el individuo es amante al riesgo y para otros es adverso. De esta manera, la función tiene una doble inflexión, que indica ese cambio de preferencias por el riesgo, siendo primero adverso, luego amante y después adverso nuevamente, tal como se observa en la ilustración 2. Estos autores tampoco definen una forma funcional, solo plantean cómo sería la forma gráfica.

Ilustración 1 Función de utilidad de von Neumann y Morgenstern (1944)

Fuente: El Alabi (2016).

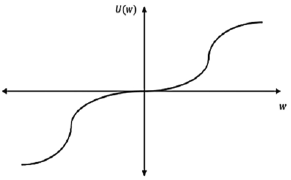
Luego, Markowitz (1952) realiza una crítica al anterior enfoque y presenta su propia curva de utilidad, que se encuentra definida tanto en la zona de ganancias como en la de pérdidas y tiene una inflexión en cada zona. Esto se da debido a que se considera que cuando se trata de montos pequeños de ganancias, las personas tienden a ser amantes del riesgo, pero cuando son montos importantes se convierten en adversos, determinando en algún punto la inflexión que marca el cambio de preferencias. Con las pérdidas ocurre lo contrario, cuando son pequeñas se tiende a ser adverso al riesgo y cuando son muy grandes se tiende a querer correr mayores riesgos (ilustración 3).

Ilustración 3. Función de utilidad de Markowitz (1952)

Fuente: El Alabi (2016).

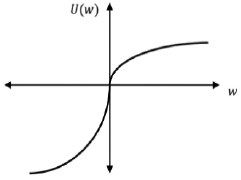
Finalmente, en 1979, Kahneman y Tversky presentan una crítica a la teoría de la utilidad esperada y presentan un modelo alternativo de decisión bajo riesgo, llamado "Prospect Theory", en el que plantean una función de utilidad en forma de S, cóncava para las ganancias y convexa para las pérdidas. Según estos autores, los agentes derivan su utilidad considerando ganancias y pérdidas, realizando la medición a partir de un punto de referencia, en lugar de tomar en cuenta la riqueza total. Esta función presenta una pendiente más inclinada para las pérdidas, reflejando la idea de que las personas son más sensibles a las pérdidas (incluso pérdidas muy pequeñas) que a las ganancias de la misma magnitud (ilustración 4).

Ilustración 4. Función de utilidad de Kahneman y Tversky (1979)

Fuente: El Alabi (2016).

3. Funciones de utilidad

Una de las primeras definiciones de funciones que permiten cuantificar el nivel de utilidad se encuentra contenida en los trabajos de Arrow (1965, 1971) y de Pratt (1964). Estos autores presentan la familia de funciones CARA (Constant Absolute Risk Aversion), la cual presenta aversión al riesgo constante respecto del nivel de riqueza total del individuo. La forma funcional propuesta se muestra en la ecuación 2.

Ecuación 2

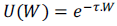Donde τ es el nivel de aversión riesgo y W es el nivel de riqueza.

A su vez, estos autores proponen que el nivel de aversión al riesgo absoluta de una función de utilidad se calcula como el ratio entre la derivada segunda y la derivada primera de la función con relación a la riqueza, tal como se expone en la ecuación 3.

Ecuación 3

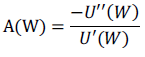Donde U'(W) es la primera derivada de la función de utilidad y U''(W) es la segunda derivada de la misma función. Así, A(W) mide la tasa a la cual la utilidad marginal decrece cuando la riqueza aumenta en una unidad. Siendo, para el caso de la función de utilidad anterior: A(W) = τ; es decir, aversión al riesgo contante absoluta (CARA) respecto del nivel de riqueza.

Por otro lado, los autores mencionados también presentan la familia de funciones de utilidad con aversión relativa al riesgo constante (CRRA por las siglas de la expresión Constant Relative Risk Aversion), que viene representada con la forma funcional de la ecuación 4.

Ecuación 4

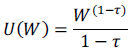Donde τ es el nivel de aversión al riesgo y W el nivel de riqueza considerado. Cuando τ = 1, la utilidad queda definida por una función logarítmica: U(W) = ln(W).

Los mismos autores definen una medida del nivel de aversión al riesgo relativa, la que proponen estimar como se expresa en la ecuación 5.

Ecuación 5

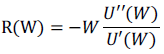En la que W es la riqueza, U'(W) es la primera derivada de la función de utilidad y U''(W) es la segunda derivada de la misma función. R(W) mide la tasa a la cual la utilidad marginal decrece cuando la riqueza aumenta en un 1 %.

La última función de utilidad presentada, que se denomina simplemente CRRA en la literatura, es ampliamente utilizada en estudios empíricos que tratan de determinar el grado de aversión al riesgo de diferentes grupos de individuos, mediante la estimación del parámetro τ. Esto se debe a que cumple con las características deseadas en una función de utilidad: es creciente, cóncava, presenta aversión relativa al riesgo constante y aversión absoluta al riesgo decreciente (DARA) (Ochoa y Vasseur, 2014). No obstante, es necesario aclarar que la función exhibe DARA solo para valores de τ mayores a cero, mientras que para valores de τ menores a cero presenta aversión al riesgo absoluta (negativa) estrictamente creciente (IARA).

Asimismo, la función CRRA implica que el sujeto no solo exhibe un valor constante de aversión al riesgo relativa para las ganancias, sino también ante pérdidas de riqueza (Milanesi, 2016).

Algunos antecedentes del uso de esta función pueden encontrarse en los siguientes trabajos: Harrison, Johnson, McInnes y Rutström (2005); Harrison, Lau y Rutstrom (2007); Harrison, Humphrey y Verschoor (2009); Harrison, Lau, Rutstrom y Tarazona-Gomez (2013); Azar y Karaguezian-Haddad (2014); Gándelman y Hernández-Murillo (2015).

En teoría, τ oscila entre -1 y 1 (Pratt, 1964), donde -1 significa que el sujeto es amante al riesgo y 1 que es adverso. Sin embargo, diferentes estudios empíricos muestran que τ toma valores dentro de un rango diferente, que va desde -0,5 a 1,25 (Pareja Vasseur y Cadavid Pérez, 2016), lo que implicaría que los comportamientos de preferencia por el riesgo no son tan extremos como en la teoría, pero la aversión se muestra aún más marcada.

Posteriormente, en 1971, Merton propone la función HARA (Hyperbolic Absolute Risk Aversion -o aversión absoluta al riesgo hiperbólica-), según la ecuación 6.

Ecuación 6

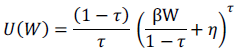Donde τ es el nivel de aversión al riesgo, β y ηson parámetros que permiten obtener distintas formas funcionales de acuerdo al valor que adopten, y W es la riqueza.

Esta función está sujeta a las restricciones: 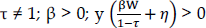. Además, η= 1 si τ = .

En el caso que τ → 1, se aplica la regla de L'Hôpital y la función se convierte en lineal: 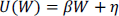; y si τ = 0 se transforma en logarítmica de la forma:.

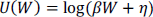Para que la función exhiba aversión al riesgo absoluta decreciente (DARA), τ debe oscilar entre y 1; si η= 0 se convierte en la función de utilidad de potencia (o CRRA) exhibiendo esa preferencia ante el riesgo; y si η= 1, se transforma en la exponencial (CARA).

Respecto de η, según el estudio empírico de Wolf y Pohlman (1983), toma valores que oscilan entre 0,243 y 0,366. Asimismo, los valores de τ se encuentran entre -0,362 y -0,180 y los de A(W) entre 1,032 y 0,824, mostrando aversión al riesgo por parte de los sujetos.

En el caso de la aversión al riesgo hiperbólica, la tolerancia al riesgo (que es la recíproca de la aversión al riesgo de Arrow y Pratt) presenta un comportamiento lineal con la riqueza (Milanesi, 2016).

Esta familia de funciones de utilidad (HARA) incluye a las cuadráticas, logarítmicas y también a las dos formas mencionadas anteriormente, esto es, la isoelástica (CRRA) y la exponencial (CARA).

Por lo tanto, HARA es una forma funcional flexible que permite representar un mayor rango de preferencias frente al riesgo que las que se pueden representar con las formas CARA y CRRA. Esto se debe a que modificando los valores de los parámetros se pueden obtener funciones de utilidad con aversión al riesgo absoluta o relativa, creciente, decreciente o constante. Esta función presenta CRRA (aversión relativa al riesgo constante) y DARA (aversión absoluta al riesgo decreciente) o IARA (aversión absoluta al riesgo creciente), dependiendo de los valores de los parámetros.

Otro aporte en este tema, se genera en 1993, cuando Saha introduce la función de utilidad Expo-Power (EP), que combina la forma exponencial con la de potencia. Su expresión se presenta en la ecuación 7.

Ecuación 7

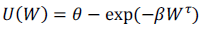Siendo θ una constante, τ el nivel de aversión al riesgo y β un parámetro adicional representando aversión al riesgo. Los parámetros están sujetos a las restricciones: θ > 1; y τ*β > 0.

En este caso, θ es solo una constante empleada para alterar la magnitud de la utilidad y no para representar una mayor cantidad de preferencias ante el riesgo. Asegura que U(W) sea positiva para todos los valores de W mayores que cero.

Asimismo, cuando τ < 1, la función exhibe DARA (aversión absoluta al riesgo decreciente), cuando τ = 1 presenta CARA (aversión absoluta al riesgo constante), y cuando τ > 1 muestra IARA (aversión absoluta al riesgo creciente). Además, cuando β < 0, exhibe DRRA (aversión relativa al riesgo decreciente) y cuando β > 0 presenta IRRA (aversión relativa al riesgo creciente).

Por otro lado, la segunda derivada de la función EP permite determinar si el individuo es adverso, neutral o amante al riesgo, según sea menor, igual o mayor a cero, respectivamente. La ecuación 8 determina el signo de la segunda derivada de la función considerada y, por consiguiente, la preferencia frente al riesgo del individuo.

Ecuación 8

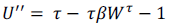Luego, Xie (2000) define la función de utilidad Power Risk Aversion (PRA). Su forma funcional está representada en la ecuación 9.

Ecuación 9

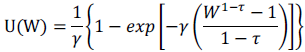Donde τ representa el nivel de aversión al riesgo y γ es un parámetro que también representa preferencias ante el riesgo. Además, la función está sujeta a las restricciones: τ ≥ 0; y γ ≥ 0.

Esta forma funcional también incluye a las funciones CARA y CRRA.

Su nombre, PRA (en el que la P representa "Power", que es la función de potencia) se justifica en el hecho de que las dos medidas de aversión al riesgo, relativa y absoluta, son funciones de potencia respecto de la riqueza. Sin embargo, mientras que el coeficiente de la aversión absoluta (A(W)) es siempre decreciente o constante en el nivel de riqueza, el coeficiente de aversión relativa al riesgo (R(W)) puede ser decreciente (cuando τ > 1), constante (cuando τ = 1) o creciente (si τ < 1).

Por otra parte, mientras más elevado sea γ, mayor será la curvatura de la función, debido a que la aversión al riesgo es lo que determina esta característica. Lo mismo ocurre con τ; la diferencia es que un mayor γ siempre implica mayor aversión, mientras que un τ más grande modifica los coeficientes de aversión al riesgo (cuando γ ≠ 0), incrementándolos para un rango de riqueza y disminuyéndolos para el otro.

Otra característica, según Xie (2000), es que la función de utilidad que él mismo propone debería representar una mejor alternativa respecto de las ampliamente utilizadas CRRA, CARA y HARA. Esto se debe a que, por un lado, no existe aún ningún estudio decisivo que valide la aceptación del supuesto de aversión al riesgo constante absoluta o relativa; y, por otro, plantea que la función de utilidad HARA es limitada en cuanto a regiones en las que se encuentra definida y es difícil de manipular debido a la complejidad de su ecuación.

Respecto de usos adicionales de la función PRA, Xie (2000) considera aplicaciones potenciales en la valoración de activos y relaciona esta función con las diferencias en las tasas de crecimiento de los diferentes países, mostrando que al permitir que el nivel de aversión relativa al riego cambie con el nivel de consumo, se puede explicar la diferencia entre dichas tasas. De todas maneras, sostiene que la aplicación de esta función a estudios microeconómicos de comportamiento humano y en valuación de activos es incluso más interesante que lo anterior.

Por último, Conniffe (2006) generaliza la función presentada por Xie, mediante la función FTP (Flexible Three Parameter), cuya expresión analítica es la de la ecuación 10.

Ecuación 10

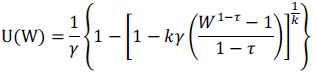Siendo W el nivel de riqueza, τ el nivel de aversión al riesgo, γ otro parámetro de aversión (cuya interpretación es igual a γ de la ecuación 9), y k una constante.

Se plantea como restricción: 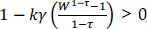, para evitar números imaginarios para valores no íntegros de 1/k.

Cuando k = 0 esta forma se reduce a la función PRA de Xie. Y cuando k = 1, se obtiene la forma lineal de aversión neutral al riesgo.

Puede exhibir IARA, DARA, CARA, IRRA, DRRA o CRRA, dependiendo de los valores que tomen los parámetros. Debido a esto, Conniffe sostiene que la función FTP puede representar un rango mayor de comportamientos frente al riesgo que el que presenta la función PRA, desarrollada por Xie.

Conniffe plantea que, para algunas combinaciones de los tres parámetros, W está limitada, ya sea por debajo (nivel mínimo) o por encima (máximo). Esto, según el autor, no es una limitación del modelo, sino que permite representar los niveles de subsistencia o de saturación de ingresos o de riqueza.

A partir de lo descripto anteriormente, se puede observar que a medida que se gana más flexibilidad en las funciones, al mismo tiempo se complejizan sus ecuaciones, debiendo incluir más parámetros para asegurar la diversidad de características deseadas ante el riesgo.

Las formas CARA y CRRA son muy simples, pero solo permiten que varíe la magnitud de la aversión al riesgo. Por otro lado, HARA, EP, PRA y FTP también permiten que varíe la magnitud de la aversión y además que la pendiente de la aversión al riesgo sea positiva o negativa. Sin embargo, esto se produce a expensas de incrementar la complejidad de las funciones (Meyer, 2007).

Por otro lado, según algunos autores, algunas funciones deben desecharse. La cuadrática y la cúbica son indeseables por presentar aversión absoluta al riesgo creciente (IARA); mientras que la exponencial negativa lo es por exhibir un comportamiento de tipo CARA y aversión relativa al riesgo creciente (IRRA) (Ochoa y Pareja Vasseur, 2014).

Además, es necesario mencionar que Wakker (2008) demuestra que la parte negativa de la función de potencia, que no suele ser considerada, permite un mejor ajuste de los datos, en el sentido de minimizar la distancia de los cuadrados entre los equivalentes ciertos observados y los que se predicen teóricamente mediante la función, siendo aún mejor que el ajuste que brinda la familia de funciones exponenciales.

A continuación, se presenta la tabla 1 que resume los comportamientos de la aversión al riesgo absoluta (A(W)) y de la relativa (R(W)) de las funciones bajo estudio. Dicha aversión puede ser creciente, constante o decreciente. En caso de que una función pueda exhibir los tres, se considera que tiene un comportamiento flexible.

Tabla 1. Cuadro comparativo del comportamiento de la aversión al riesgo de las funciones de utilidad

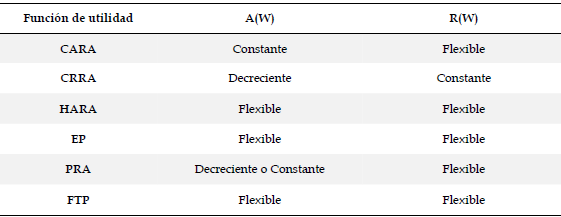
Fuente: elaboración propia.

4. Análisis de sensibilidad de la utilidad y de la aversión al riesgo

En esta sección se realiza un análisis de sensibilidad univariado, a partir de la utilización de las funciones presentadas anteriormente. El objetivo es estudiar el comportamiento de la utilidad ante cambios en los valores de la riqueza, y también el comportamiento de los coeficientes de aversión al riesgo, tanto absoluta como relativa, frente a los mismos cambios en la riqueza. En este tipo de análisis univariados, se producen cambios solamente en una de las variables independientes, céteris páribus el resto, para evaluar el efecto sobre las variables de interés, en este caso, la utilidad y la aversión.

En la tabla 2 se indican los valores tomados para cada uno de los parámetros de las funciones bajo análisis, con el objetivo de realizar las ilustraciones posteriores. Estos valores se determinan ad hoc, utilizando el mismo valor de τ en todas las funciones y estableciendo valores para los restantes parámetros que cumplan con las restricciones de cada caso.

Tabla 2. Valores de los parámetros utilizados para graficar

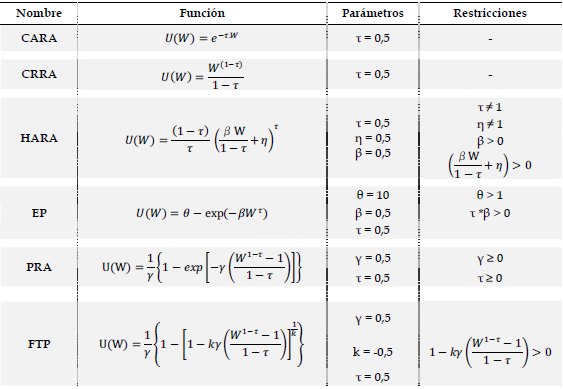
Fuente: elaboración propia.

Tal como puede observarse en la ilustración 5, las funciones de utilidad CRRA y HARA son las que presentan mayores cambios en el nivel de satisfacción por cambios en el nivel de riqueza. En los casos de las funciones EP, PRA y FPT los cambios marginales en la utilidad son casi imperceptibles en el entorno gráfico ilustrado, esto implica que la derivada parcial de la utilidad en relación a la riqueza es positiva, pero muy cercana a cero sobre todo para niveles elevados de riqueza. De hecho, las funciones PRA y FPT se encuentran casi solapadas en un buen tramo del rango de valores de la riqueza.

Ilustración 5. Funciones de utilidad ante cambios en la riqueza

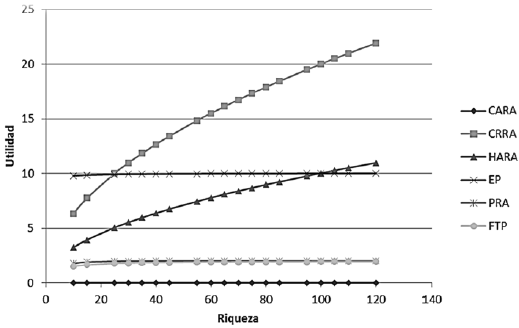
Fuente: elaboración propia.

Como se puede observar en la ilustración 6, todas las funciones de utilidad consideradas, excepto CARA, muestran un comportamiento decreciente de la aversión absoluta al riesgo (DARA), característica deseada en una buena función de utilidad.

Ilustración 6. Aversión absoluta al riesgo en función de la riqueza

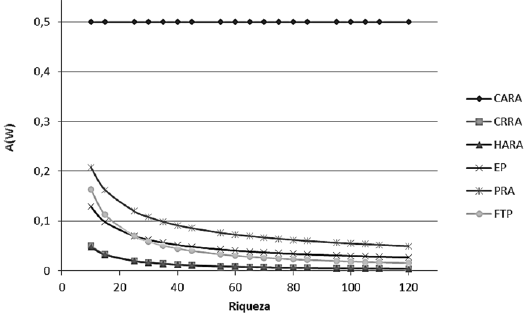
Fuente: elaboración propia.

CARA, como su nombre lo indica, presenta aversión absoluta al riesgo contante para todos los niveles de riqueza, con lo que no refleja el comportamiento deseado. Esto se debe a que, para el caso de dicha función, la medida de aversión al riesgo A(W) es igual al coeficiente de aversión al riesgo (τ), quedando A(W) definida por una constante.

Además, se aprecia que al principio las aversiones presentadas por las funciones disminuyen más rápidamente, debido a que mientras menos riqueza se posee más adverso al riesgo se es, entonces a medida que se incrementa el nivel de riqueza acumulada, la aversión absoluta va disminuyendo, correspondientemente con lo planteado en la teoría.

En la ilustración 7, se muestra la aversión relativa al riesgo que presentan las funciones de utilidad frente a diferentes valores de riqueza. En este sentido, dentro de las características deseadas de este tipo de funciones, se encuentra que exhiba aversión relativa al riesgo constante respecto de los niveles de riqueza, cuestión que se cumple para las funciones HARA, CRRA y FPT (esta última con pequeñas fluctuaciones). Pero las funciones CARA, EP y PRA presentan aversión relativa al riesgo creciente (IRRA), sobre todo la primera, que crece abruptamente con la riqueza, separándose de las demás. Esto último se debe a que R(W) es igual A(W) multiplicado por la riqueza, con lo que para el caso de CARA que presenta A(W) constante, R(W) presenta un crecimiento directamente proporcional a la riqueza.

Ilustración 7. Aversión al riesgo relativa en función de la riqueza

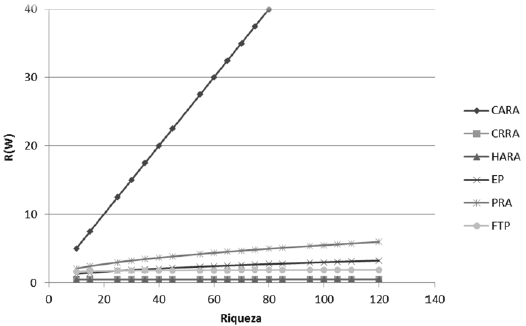
Fuente: elaboración propia.

5. Comentarios finales

En este trabajo se ha presentado un compendio no exhaustivo de los antecedentes teóricos en materia de funciones de utilidad, mostrando a su vez distintas formas funcionales que pueden ser utilizadas para representar utilidad, propuestas por diversos autores.

El análisis de los hallazgos permite afirmar que a medida que ganan flexibilidad, las funciones de utilidad también se complejizan, agregando parámetros adicionales, que pueden representar preferencias ante el riesgo, para que las funciones cumplan con las características deseadas por sus autores.

Es necesario mencionar que, aunque las funciones CRRA, HARA y FPT cumplen con los postulados deseados de aversión absoluta al riesgo decreciente ante aumentos en la riqueza y aversión relativa al riesgo constante, en la estimación del riesgo mediante estudios empíricos, la función CRRA es la utilizada en mayor medida. Esto último se debe a su simplicidad en relación con las otras formas funcionales. HARA también se emplea, aunque en menor medida. Sobre esta última, se destaca su uso para el desarrollo de otros temas de la teoría económica tales como determinación de tasas de descuento y valuación de activos.

Entre las limitaciones, es necesario destacar que se trata de un estudio preliminar no exhaustivo, lo que atenta contra la definición precisa de algunos parámetros en determinadas formas funcionales. Asimismo, la comparación entre las funciones presentadas se realiza en el campo de lo teórico (a pesar de simular comportamientos en la sección 4), lo cual no permite llegar a conclusiones rotundas sobre la precisión del ajuste de dichas funciones a las preferencias reales de los individuos.

Como futuras líneas de investigación, se propone profundizar el estudio realizado, incluyendo un mayor número de funciones, así como el testeo empírico de sus parámetros localmente. A posteriori, se abordarán otros conceptos que podrían influir en el proceso decisorio de consumo e inversión de los individuos, tales como la racionalidad limitada, los sesgos y las heurísticas.

Referencias
1. Arrow, K. J. (1965). Aspects of the theory of risk-bearing. Yrjö Jahnssonin Säätiö .
2. Arrow, K. J. (1971). The theory of risk aversion. En Essays in the theory of risk-bearing (pp. 90-120). Chicago: Markham Publishing.
3. Azar, S. A., & Karaguezian-Haddad, V. (2014). Simulating the market coefficient of relative risk aversion. Cogent Economics & Finance, 2(1), 990742. Disponible en: https://www.cogentoa.com/article/10.1080/23322039.2014.990742.pdf
4. Bernoulli, D. (1738). Exposition of a New Theory on the Measurement of Risk. Econométrica 1954, 22(1), pp. 23-36. Disponible en: https://engineering.purdue.edu/~ipollak/ece302/FALL09/notes/Bernoulli_1738.pdf
5. Carcámo, U. (2016). Los fundamentos matemáticos de la teoría de las finanzas (ii): incluyendo incertidumbre y riesgo. Semestre Económico, pp. 123-158. Disponible en: http://www.redalyc.org/pdf/1650/165013657005.pdf
6. Conniffe, D. (2006). The flexible three parameter utility function. Annals of Economics and Finance, 8(1), 57-63. Disponible en: http://aeconf.com/articles/ may2007/aef080104.pdf
7. El Alabi, E. (2016). Los montos importan: una curva de utilidad alternativa (Tesis presentada para acceder al grado de Doctor en Ciencias de la Administración), Universidad Nacional del Sur. Disponible en: http://repositoriodigital.uns.edu.ar/bitstream/123456789/2649/1/Tesis%20Doctoral%20-%20Emilio%20El%20Alabi.pdf
8. Friedman, M., & Savage, L. J. (1948). The utility analysis of choices involving risk. The journal of political economy, 56, pp. 279-304. Disponible en: https://econpapers.repec.org/article/ucpjpolec/v_3a56_3ay_3a1948_3ap_3a279.htm
9. Gándelman, N., & Hernández-Murillo, R. (2015). Risk aversion at the country level. [Working Paper 2014-005B]. Federal Reserve Bank of St. Louis, Research Division, St. Louis, MO. Disponible en: http://citeseerx.ist.psu.edu/ viewdoc/download?doi=10.1.1.589.9180&rep =rep1&type=pdf
10. Harrison, G. W., Humphrey, S. J., & Verschoor, A. (2009). Choice under uncertainty: evidence from Ethiopia, India and Uganda. The Economic Journal, 120(543), pp. 80-104.
11. Harrison, G. W., Johnson, E., McInnes, M. M., & Rutstrom, E. E. (2005). Individual choice and risk aversion in the laboratory: comment. The American Economic Review, 95(3), 897-901. Disponible en: http://citeseerx.ist.psu.edu/ viewdoc/download?doi=10.1.1.469.509& rep=rep1&type=pdf
12. Harrison, G. W., Lau, M. I., & Rutstrom, E. E. (2007). Estimating risk attitudes in Denmark: a field experiment. The Scandinavian Journal of Economics, 109(2), pp. 341-368. Disponible en: https://pdfs.semanticscholar.org/df52/ 40bb1f0bef65b41bc1006ac31aaeb7358db3.pdf
13. Harrison, G. W., Lau, M. I., Rutstrom, E. E., & Tarazona-Gomez, M. (2013). Preferences over social risk. Oxford Economic Paper, 65(1), 25-46. Disponible en: https://www.itd.bus.ucf.edu/cdn/economics/workingpapers/2005-06.pdf
14. Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica: Journal of the econometric society, 47(2), pp. 263-291. Disponible en: https://www.princeton.edu/~kahneman/docs/Publications/ prospect_theory.pdf
15. Markowitz, H. (1952). The utility of wealth. The Journal of Political Economy, 60, pp. 151-158. Disponible en: https://econpapers.repec.org/article/ ucpjpolec/v_3a60_3ay_3a1952_3ap_3a151.htm
16. Merton, R. C. (1971). Optimum consumption and portfolio rules in a continuous-time model. Journal of economic theory, 3(4), 373-413. Disponible en: http://www.people.hbs.edu/rmerton/Optimum%20Consumption%20and %20Portfolio%20Rules.pdf
17. Meyer, J. (2007). Representing risk preferences in expected utility based decision models. Annals of Operations Research, 176(1), 179-190. Disponible en: http://ageconsearch.umn.edu/bitstream/9380/1/cp07me02.pdf
18. Milanesi, G. (2016). Un modelo de opciones reales y funciones de utilidad isoelásticas para valorar I&D en mercados incompletos (Documento de trabajo). Universidad Nacional del Sur.
19. Ochoa, C. M., & Pareja Vasseur, J. (2014). Valoración de opciones reales a través de equivalentes de certeza. Revista Ecos de Economía, 18(39), pp. 49-72. Disponible en: http://www.scielo.org.co/pdf/ecos/v18n39/v18n39a03.pdf
20. Autora (2011). Incertidumbre y riesgo. En F. Rotstein (Ed.), Decisiones de inversión: métodos de evaluación, riesgo y flexibilidad estratégica (pp. 10-128). Bahía Blanca: Induvio Editora.
21. Pareja Vasseur, J. y Cadavid Pérez, C. (2016). Valoración de patentes farmacéuticas a través de opciones reales equivalentes de certeza y función de utilidad. Contaduría y Administración, 61(4), 794-814. Disponible en: http://www.redalyc.org/pdf/395/39546934011.pdf
22. Pratt, J. W. (1964). Risk-aversion in the small and in the large. Econometrica, 32(1-2), 122-136. Disponible en: http://www2.econ.iastate.edu/classes/econ642/Babcock/pratt.pdf
23. Saha, A. (1993). Expo-power utility: A 'flexible' form for absolute and relative risk aversion. American Journal of Agricultural Economics, 75(4), 905-913.
24. Saha, A., Shumway, C. R., & Talpaz, H. (1994). Joint estimation of risk preference structure and technology using expo-power utility. American Journal of Agricultural Economics, 76(2), 173-184. Disponible en: https://www.jstor.org/ stable/1243619?seq=1#page_scan_tab_contents
25. Von Neumann, J. & Morgenstern, O. (1944). Theory of Games and Economic Behavior. Princeton University Press, Estados Unidos.
26. Wakker, P. P. (2008). Explaining the characteristics of the power (CRRA) utility family. Health Economics, 17(12), 1329-1344.
27. Wolf, C., & Pohlman, L. (1983). The recovery of risk preferences from actual choices. Econometrica: Journal of the Econometric Society, 51(6), 843-850. Disponible en: https://www.jstor.org/stable/1912107?seq=1#page_scan_tab _contents
28. Xie, D. (2000). Power Risk Aversion Utility Functions. Annals of Economics and Finance, 1, 265-282. Disponible en: http://aeconf.com/Articles/Nov2000/ aef010202.pdf

© 2016 por los autores; licencia otorgada a la revista Escritos Contables y de Administración. Este artículo es de acceso abierto y distribuido bajo los términos y condiciones de una licencia Atribución-No Comercial 4.0 Internacional (CC BY-NC 4.0) de Creative Commons. Para ver una copia de esta licencia, visite https://creativecommons.org/licenses/by-nc/4.0/