On a quasilinearisation method for the Von Kärmkän flow problem with heat transfer

Z. G. Makukula^†, P. Sibanda^† and S. S. Motsa^‡

† School of Mathematical Sciences, University of KwaZulu-Natal, Private Bag X01, Scottsville 3209
Pietermaritzburg, South Africa. sibandap@ukzn.ac.za
‡ Department of Mathematics, University of Swaziland, Private Bag 4-, Kwaluseni, Swaziland
sandilemotsa@gmail.com

Abstract— A quasilinearisation method for solving the nonlinear equations is presented. The method works successively in linearizing the nonlinear equations and solving the resulting higher order deformation equations using spectral methods. We illustrate the application of the method by solving the laminar heat transfer problem in a rotating disk. Comparison between the linearisation method and numerical results obtained using the MATLAB in-built bvp4c solver reveals that the linearisation method is accurate and converges at very low orders of the iteration scheme.

Keywords— Heat Transfer; Linearisation Method; Rotating Disk; Spectral Methods.

INTRODUCTION

Disk-shaped bodies are encountered in many engineering, geophysical and meteorological applications. The study of fluid flow due to a rotating disk was pioneered by von Karman (1921) who provided the basis for the mathematical study of the rotating disk problem in an incompressible viscous flow of infinite extent. He introduced transformations that reduced the governing partial differential equations to ordinary differential equations. Since then, solutions of the von Karman equations describing different aspects of the disk flow problem such as the effect of combined viscous dissipation and joule heating in the presence of Hall and ion-slip currents, the effect of suction on the flow with or without an applied magnetic field and thermal and mass diffusive effects have been of interest to researchers in diverse fields of science.

As with most problems in science and engineering, the equations that describe swirling flow are nonlinear and do not have closed form solutions. In most instances the von Karman equations have been solved numerically using either the shooting method or the implicit finite difference scheme in combination with a linearisation technique. While numerical methods are effective and give accurate solutions, they often give no insights into the structure of the solution, particularly the effects of multi-parameters embedded in the problem. Numerical methods also often fail to give sufficient resolution to domains with very sharp changes or to problems with multiple solutions. These limitations necessitate the development of computationally improved semi-analytical methods for solving strongly nonlinear problems. Recent semi-analytical methods include, among others, the variational iteration method and the homotopy perturbation method (He, 2000, 2007), the Adomian decomposition method (Adomian, 1976), the homotopy analysis method (Liao, 2003) and the spectral-homotopy analysis methods (Motsa et al., 2010). These methods may converge slowly or fail to converge for problems that are strongly nonlinear or for problems with very large parameters.

In this paper we present a method for solving nonlinear equations that is based on iteratively linearizing the equations to obtain a system of higher order deformation equations that are solved using spectral methods. The application of the method is demonstrated by solving the laminar heat transfer problem in a rotating disk. The problem was studied by Shevchuk and Buschmann (2005) who solved the transformed ordinary differential equations using a numerical method. Other recent studies on various aspects of the rotating disk flow problem include the works of Takhar et al. (2002) who considered electrically conducting fluids in MHD flow and Arikoglu and Ozkol (2006) who considered heat transfer characteristics on MHD flow. The series of studies by Attia (2004, 2006, 2007) considered the effects of (i) ion slip, (ii) temperature dependent viscosity and (iii) ohmic heating on rotating disk flow. Sibanda and Makinde (2010) considered the effects of ohmic and viscous heat dissipation, Hall currents, porosity and an applied magnetic field on a rotating disk flow with constant properties.

II. GOVERNING EQUATIONS

We consider a disk rotating with angular velocity ω in a fluid which rotates in the same direction with a different angular velocity Ω. In cylindrical polar coordinates (r,∅ z) the Navier-Stokes equations governing the flow are (Schlichting, 1979);

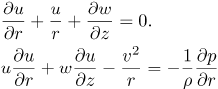	(1)
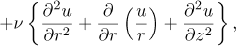	(2)
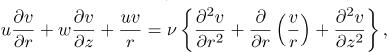	(3)
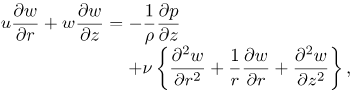	(4)
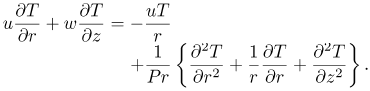	(5)

The boundary conditions are

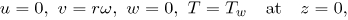	(6)
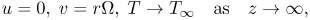	(7)

where u, v and w are the velocity components in the radial, tangential and axial directions respectively, ν is the kinematic viscosity, ρ is the density, p is the static pressure, T is the temperature and the subscripts w and ∞ refer to the wall and the outer boundary layer edge respectively, and Pr is the Prandtl number. We introduce a dimensionless coordinate 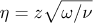and the von Kármán transformations;

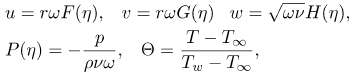(8)

where F, G and H are the dimensionless velocity components along the radial, tangential and axial directions respectively and Θ is the dimensionless temperature. The radial pressure gradient can be computed for the frictionless flow at a large distance from the wall using the condition:

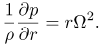(9)

Shevchuk and Buschmann (2005) showed that by using the transformations (8), the Navier-Stokes equations reduce to the following system of nonlinear ordinary differential equations,

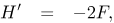	(10)
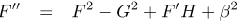	(11)
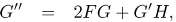	(12)
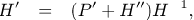	(13)
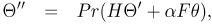	(14)

with boundary conditions

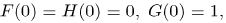	(15)
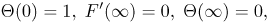	(16)
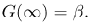	(17)

Using (10), equations (11), (12) and (14) can be expressed as

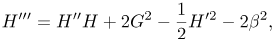	(18)
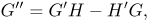	(19)
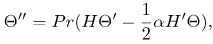	(20)

subject to

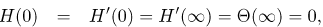	(21)
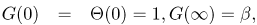	(22)

where α is a constant and Β = Ω/ω is the flow swirl parameter. Equation (13) can be used to find the pressure.

III. METHOD OF SOLUTION

The quasilinearisation method (see Makukula et al. 2010a-e, Motsa and Shateyi, 2010, Shateyi and Motsa, 2010) is applied to solve equations (18) - (20). The starting point is to assume that the independent variables H(η) , G(η) and Θ(η) may be expanded as

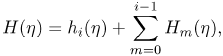	(23)
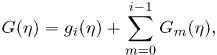	(24)
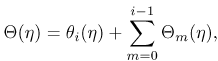	(25)

where h_i g_i and θ_i(i = 1, 2, 3,...) are unknown functions and H_m , G_m and Θ_m (m ≥ 1) are approximations that are obtained by recursively solving the linear part of the equation that results from substituting (23) - (25) into equations (18) - (20). This gives the equations,

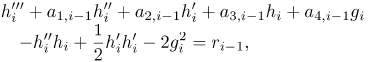	(26)
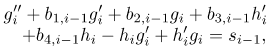	(27)
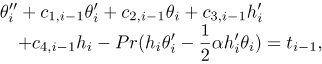	(28)

where the coefficient parameters 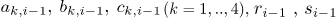, and 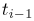, are defined as

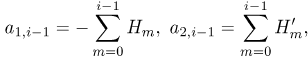	(29)
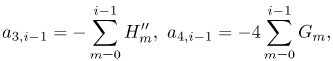	(30)
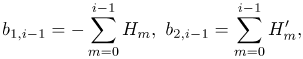	(31)
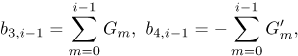	(32)
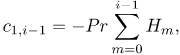	(33)
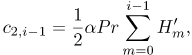	(34)
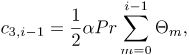	(35)
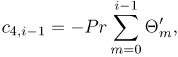	(36)
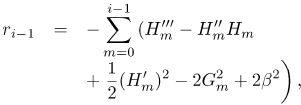	(37)
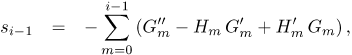	(38)
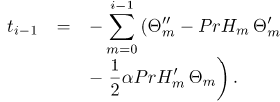	(39)

Starting from the initial approximations

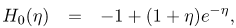	(40)
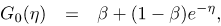	(41)
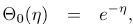	(42)

which are chosen to satisfy the boundary conditions (21) - (22), the subsequent solutions for H_m, G_m, Θ_m, m ≥ 1 are obtained by successively solving the linearized form of equations (26), (27) and (28) subject to the boundary conditions

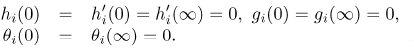(43)

Once each solution h_i, g_i and θ (i ≥ 1) has been found, the approximate solutions for H (η) , G(η) and Θ(η) are obtained as

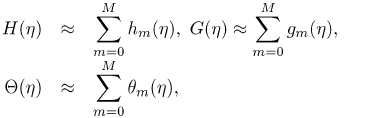(44)

where M is the order of the approximation.

Equations (26) - (28) are integrated using the Chebyshev spectral collocation method. The unknown functions are defined by the Chebyshev interpolating polynomials with the Gauss-Lobatto points defined as

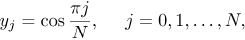(45)

where N is the number of collocation points used. The physical region [0, ∞] is transformed into the domain [—1,1] using the domain truncation technique in which the problem is solved on the interval [0, L] instead of [0, ∞). This leads to the mapping

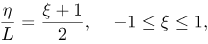(46)

where L is the scaling parameter used to invoke the boundary condition at infinity. The unknown functions hi, gi and are approximated at the collocation points by

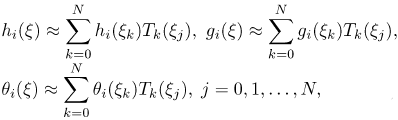(47)

where T_k is the kth Chebyshev polynomial defined as

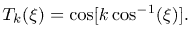(48)

The derivatives of the variables at the collocation points are represented as

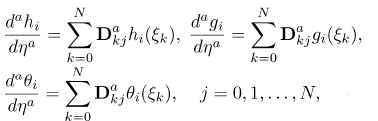(49)

where α is the order of differentiation and 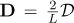with 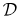being the Chebyshev spectral differentiation matrix (see Canuto et al., 1988 and Trefethen, 2000). This leads to the matrix equation

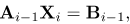(50)

in which 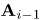is a (3N + 3) x (3N + 3) square matrix and X_i and B_i-1 are (3N + 3) x 1 column vectors defined by

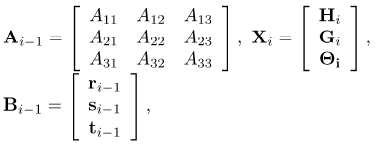(51)

with

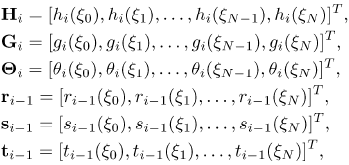
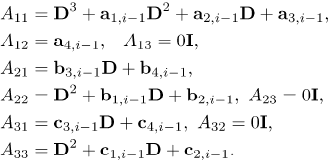
In the definitions above, 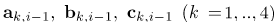are diagonal matrices of size (N + 1) x (N + 1) and I is the (N + 1) x (N + 1) identity matrix. After modifying the matrix system (50) to incorporate boundary conditions, the solution is obtained as

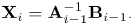(52)

IV. RESULTS AND DISCUSSION

A quasilinearisation method (the SLM) has been used to solve the nonlinear equations for the rotating disk problem. The accuracy of the method is determined by benchmarking the results with numerical results obtained using the bvp4c, an in-built MATLAB solver for boundary value problems. This solver is based on the fourth order Runge-Kutta schemes. The results were generated using N = 150 and L = 30 which was found to give good accuracy. Tables 1 - 4 show the results of the laminar heat transfer problem for a rotating disk in a forced vortex. Table 1 gives a sense of the convergence rate of the linearisation method through a comparison of the values of the axial velocity H(∞) at different orders of the SLM approximation and for different values of Β against the numerical results. Simulations show a decrease in the magnitude of the axial velocities with the swirl parameter /?. Convergence up to seven decimal places of the linearized results to the numerical results is achieved at the third order of the SLM approximation.

Table 1: Comparison of the values of the SLM solutions for H(00) with the bvp4c solutions when a = 0.25 and Pr = 0.71.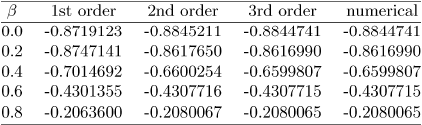

Table 2: Comparison of the values of the SLM solutions for 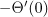with the bvp4c solutions when α = — 1 and Β = 0.2.

Table 3: Comparison of the values of the SLM solutions for 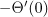with the bvp4c solutions when Pr = 0.71 and Β= 0.2.

Table 4: Comparison of the values of the SLM solutions for 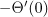with the bvp4c solutions when Pr = 5 and α = 4.

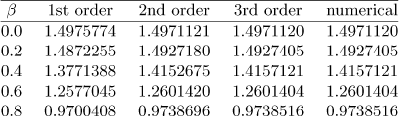
Table 2 shows the effect of increasing Prandtl numbers on the heat transfer rate. The heat transfer rate evidently increases with Prandtl numbers. A similar patten is observed in Table 3 where 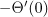increases with α.

Increasing the swirl parameter Β in Table 4 results in the surface heat transfer rate being reduced. In terms of the accuracy of the linearisation method, it is evident that convergence of the SLM results up to seven decimal place accuracy is achieved at the third order of the SLM approximation. Figures 1-4 show the results for the laminar heat transfer problem of a rotating disk in a forced vortex. Figures 1-2 show the effect of Β on the radial and axial velocity profiles respectively. Here the third order SLM approximations are plotted alongside the numerical solution. We observe an excellent agreement between the SLM and the numerical results and the results show that increasing

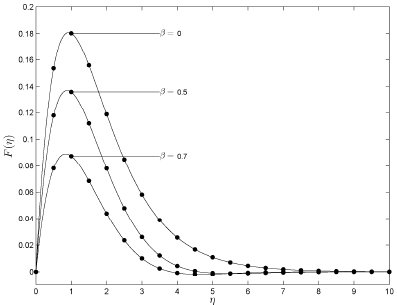
Figure 1: Comparison between the 3rd order (filled circles) and the numerical solutions (solid line) for F(η) when α = 1 and Pr = 0.25.

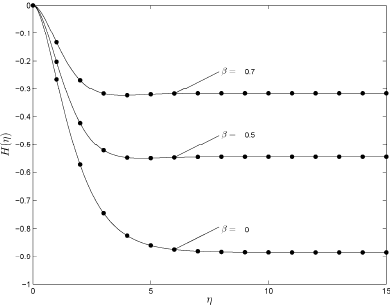
Figure 2: Comparison between the 3rd order (filled circles) and the numerical solutions (solid line) for G (η)when α = 1 and Pr = 0.25.

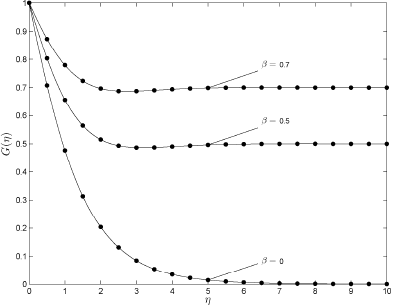
Figure 3: Comparison between the 3rd order solution (filled circles) and the numerical solution (solid line) for G(η) when a = 1 and Pr = 0.25.

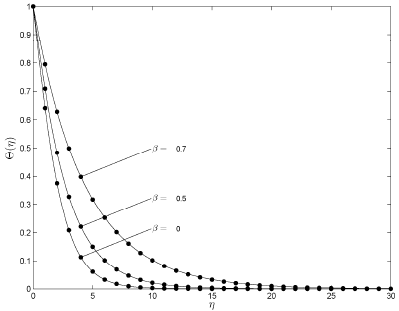
Figure 4: Comparison between the 3rd order solution (filled circles) and the numerical solution (solid line) for Θ(η) when α = 1 and Pr = 0.25.

the swirl parameter Β reduces the radial velocity while increasing the axial velocity. It is worth noting here that the radial velocity profiles given in Shevchuk and Buschmann (2005) are not consistent with some previous results in the literature, for example, those of Attia (2008) and Turkyilmazoglu (2010). Figures 3 - 4 show the effect of Β on the tangential velocity profile G(η) and the temperature Θ(η) for fixed Prandtl numbers. The agreement between the third order SLM approximations and the numerical solutions excellent. An increase in the swirl parameter leads to an increase in both the temperature and the tangential velocity profiles.

V. CONCLUSION

A successive linearisation algorithm to compute the numerical solution for the laminar heat transfer problem of a rotating disk in a forced vortex has been presented. Values of the axial velocity far from the surface of the disk were obtained for various swirl parameter values Β. An increase in H(η) was observed with increase in Β. The heat transfer rate was found for different Prandtl numbers and Β. The heat transfer rate increases with increase in the Prandtl number but decreases with Β. The axial and tangential velocity and the temperature profiles were found to increase with Β while the radial velocity profiles decreased with Β. The linearisation method was found to be accurate and rapidly convergent to the numerical results.

ACKNOWLEDGMENT
The authors wish to acknowledge financial support from the National Research Foundation (NRF).

REFERENCES
1. Adomian, G., "Nonlinear stochastic differential equations," J Math. Anal. Appl. 55, 441 - 52 (1976).
2. Arikoglu, A. and I. Ozkol, "On the MHD and slip flow over a rotating disk with heat transfer," Int. Num. J. Heat & Fluid Flow, 16, 172-184 (2006).
3. Attia, H.A., "Ion slip effect on the flow due to a rotating disk," The Arab. J. Sci. and Eng., 29, 165 - 172 (2004).
4. Attia, H.A., "Unsteady flow and heat transfer of viscous incompressible fluid with temperature-dependent viscosity due to a rotating disc in a porous medium," J. Phys. A: Math. Gen., 39, 979 - 991 (2006).
5. Attia, H.A., "Rotating disk flow and heat transfer of a conducting non-Newtonian fluid with suction-injection and ohmic heating," J. Braz. Soc. Mech. Sci. and Eng., 19, 168 - 173 (2007).
6. Attia, H.A., "Rotating disk flow and heat transfer through a porous medium of a non-Newtonian fluid with suction and injection," Comm. Nonlinear Sc. Num. Simul., 13, 1571 - 1580 (2008).
7. Canuto, C., M.Y. Hussaini, A. Quarteroni, and T.A. Zang, Spectral Methods in Fluid Dynamics, Springer-Verlag, Berlin (1988).
8. He, J.H., "A coupling method for homotopy technique and perturbation technique for non-linear problem," Int. J. Non-Linear. Mech., 35, 37 - 43 (2000).
9. He, J.H. and X.H. Hu, "Variational iteration method: New development and applications," Computers and Mathematics with Applications, 54, 115 - 123 (2007).
10. Liao, S.J., Beyond perturbation: Introduction to homotopy analysis method. CRC Press (2003).
11. Makukula, Z.G., P. Sibanda and S.S. Motsa, "On a new solution for the viscoelastic squeezing flow between two parallel plates," Journal of Advanced Research in Applied Mathematics, 2, 31 - 38 (2010a).
12. Makukula, Z.G., P. Sibanda and S.S. Motsa, "A note on the solution of the von Karman equations using series and Chebyshev spectral methods," Mathematical Problems in Engineering, doi: 10.1155/2010/528956 (2010b).
13. Makukula, Z.G., P. Sibanda, S.S. Motsa, "A novel numerical technique for two-dimensional laminar flow between two moving porous walls," Mathematical Problems in Engineering, doi: 10.1155/2010/528956 (2010c).
14. Makukula, Z.G., P. Sibanda, S.S. Motsa, "A note on the solution of the von Krmn equations using series and Chebyshev spectral methods," Boundary Value Problems, doi:10.1155/2010/471793 (2010d).
15. Makukula, Z.G., P. Sibanda, S.S. Motsa, "On new solutions for heat transfer in a visco-elastic fluid between parallel plates," International Journal of Mathematical Models and Methods in Applied Sciences, 4, 221 - 230 (2010e).
16. Motsa, S.S. and S. Shateyi, "A new approach for the solution of three-dimensional magneto-hydrodynamic rotating flow over a shrinking sheet," Mathematical Problems in Engineering, doi: 10.1155/2010/586340 (2010).
17. Motsa, S.S., P. Sibanda and S. Shateyi, "A new spectral-homotopy analysis method for solving a nonlinear second order BVP," Commun. Nonlinear Sci. Numer. Simul., 15, 2293 - 2302 (2010).
18. Shateyi, S. and S.S. Motsa, "Variable viscosity on magnetohydrodynamic fluid flow and heat transfer over an unsteady stretching surface with Hall effect," Boundary Value Problems, doi: 10.1155/2010/257568 (2010).
19. Schlichting, H., Boundary layer theory, McGraw Hill, NY (1979).
20. Shevchuk, I.V. and M.H. Buschmann, "Rotating disk heat transfer in a fluid swirling as a forced vortex," Heat Mass Transfer, 41, 1112 - 1121 (2005).
21. Sibanda, P. and O.D. Makinde, "On MHD flow and heat transfer past a rotating disk in a porous medium with ohmic heating and viscous dissipation," International Journal of Numerical Methods for Heat & Fluid Flow, 20, 269 - 285 (2010).
22. Takhar, H.S., A.K. Sing and G. Nath, "Unsteady MHD flow and heat transfer on a rotating disk in an ambient fluid," Int. J. Therm. Sci., 41, 147 -155 (2002).
23. Trefethen, L.N., Spectral Methods in MATLAB, SIAM (2000).
24. Turkyilmazoglu, M., "Unsteady mhd flow with variable viscosity: Applications of spectral scheme," Int. J. Therm. Sci., 49, 563 - 570 (2010).
25. von Karman, T., "Uberlaminare und turbulence reibung," ZAMM, 1, 233 - 252 (1921).

Received: December 15, 2010.
Accepted: May 16, 2011.
Recommended by Subject Editor Walter Ambrosini.