Influences of temperature dependent viscosity and thermal conductivity on the unsteady flow and heat transfer of a micropolar fluid over a stretching sheet

M. Modather^†‡ , A. M. Rashad^† and S. M. M. El-Kabeir^†‡

^† Department of Mathematics, South Valley University, Faculty of Science, Aswan, Egypt.
^‡ Department of Mathematics, College of Science and Humanitarian Studies, AL-Kharj University, Saudi Arabia.
am_rashad@yahoo.com

Abstract — This paper is devoted to describe the analysis of unsteady boundary layer flow and heat transfer of a viscous, incompressible micropolar fluid having temperature-dependent viscosity and thermal conductivity over a non-isothermal horizontal stretching sheet. The fluid viscosity and the thermal conductivity are assumed to vary as inverse linear functions of temperature. The unsteady boundary layer equations for the momentum, angular momentum and thermal energy are simplified using suitable transformations. The resulting system of nonlinear ordinary differential equations is solved numerically by employing a shooting technique with fourth order Runge-Kutta integration scheme. The effects of the various parameters on the velocity, microrotation and temperature profiles are presented graphically. In addition, tabulated results for the skin-friction coefficient, Nusselt number and couple stress at the plate are presented and discussed.

Keywords — Unsteady Flow; Micropolar Fluid; Stretching Sheet; Temperature Dependent Viscosity and Thermal Conductivity.

I. INTRODUCTION

The theory of microfluids, as developed by Eringen (1964) has been a field of active research for the last few decades as this class of fluids represents mathematically many industrially important fluids, like paints, blood, body fluids, polymers, colloidal fluids and suspension fluids. This theory takes into account the initial characteristics of the substructure particles which are allowed to undergo rotation. Micropolar fluids are fluids with microstructure belonging to a class of fluids with non-symmetrical stress tensor. Physically, they represent fluids consisting of randomly oriented particles suspended in a viscous medium. Gorla (1995) has studied the unsteady mixed convection in micropolar boundary-layer flow over a vertical surface where unsteadiness arises as a result of time-varying nature of the free stream velocity as well as the wall temperature. Kim (2001) considered unsteady convection flow of micropolar fluid past a vertical porous plate embedded in a porous medium. The flow of a magneto-micropolar fluid past a continuously moving plate is analyzed by Seddeek (2003). The study of the mixed convection flow of a continuously moving flat plate placed in a parallel moving stream of a micropolar fluid was provided by Bhargava et al. (2003). The natural convection flow of a micropolar fluid past a continuously moving vertical porous flat plate has been studied numerically by Rahman and Sattar (2006). Ishak et al. (2007) have studied the problem of steady boundary-layer flow of a micropolar fluid on a continuously moving or fixed permeable surface. EL-Kabeir and Gorla (2007) studied the effects of transverse magnetic field on natural convection of a micropolar fluid-saturated porous medium around heated vertical surfaces. The steady two-dimensional mixed convection flow of a micropolar fluid over a non-linear stretching sheet is investigated by Hayat et al. (2008). Patil and Kulkarni (2008). The steady mixed convection boundary layer flow over a vertical surface immersed in an incompressible micropolar fluid is considered by Ishak et al. (2009).

Most of the existing analytical studies for this problem are based on the constant physical properties of the ambient fluid. However, it is known (see, Herwing and Gersten, 1986) that these properties may change with temperature, especially for fluid viscosity. To accurately predict the flow and heat transfer rates, it is necessary to take into account this variation of viscosity and thermal conductivity. Hossain and Munir (2001) studied the natural convection flow of a viscous fluid about a truncated cone with temperature dependent viscosity and thermal conductivity. The interaction of forced convection and thermal radiation during the flow of a surface moving continuously in a flowing stream of micropolar fluid with variable viscosity have been considered by EL-Kabeir (2004). Elbarbary and Elgazery (2004) studied the effects of variable viscosity and variable thermal conductivity on heat transfer from moving surfaces in a micropolar fluid. Hassanien et al. (2003) investigated variable viscosity and thermal conductivity effects on combined heat and mass transfer in mixed convection over a wedge in porous media. The effects of variable viscosity and thermal conductivity effects on MHD flow and heat transfer in viscoelastic fluid over a stretching sheet were investigated by Salem (2007). Rahman and Sattar (2007) studied the transient convective flow of micropolar fluid past a continuously moving vertical porous plate in the presence of radiation Elgazery (2009) analyzed the effects of variable viscosity and thermal diffusivity on MHD flow of a micropolar fluid under the effects of chemical reaction, Hall and ion-slip currents.

The present investigation is concerned with the effects of temperature-dependent viscosity and thermal conductivity on an unsteady two-dimensional laminar flow of a micropolar fluid from a non-isothermal stretching sheet. In formulating the equations governing the flow both the viscosity and the thermal conductivity of the fluid are considered to be linear function of temperature. The governing differential equations are transformed into a dimensionless form using similarity variables and then solved numerically by employing a shooting method. The effects of the various parameters such as, the variable viscosity, thermal conductivity and unsteady and micropolar parameters on the velocity, microrotation and temperature profiles are presented graphically. In addition, tabulated results for the skin-friction coefficient, Nusselt number and wall couple stresses at the plate are presented and discussed.

II. MATHEMATICAL FORMULATION

Consider the unsteady two-dimensional laminar flow of a viscous incompressible micropolar fluid with temperature dependent viscosity and thermal conductivity past a semi-infinite stretching sheet in the region y > 0, as shown in Fig. 1. Keeping the origin fixed, two equal and opposite forces are suddenly applied along the x- axis, which results in stretching of the sheet and hence, flow is generated. At the same time, the wall temperature of the sheet is suddenly raised from T_∞ to T_w(t,x)(> T_∞). As stated in the introduction, the fluid properties are assumed to be constant, except for the fluid viscosity and thermal conductivity which are taken as a linear function of temperature. Then under the usual boundary layer approximations, the governing equations for the problem can be written as follows, see Elbashbeshy and Bazid (2004) and Sharidan et al. (2006):

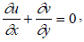	(1)
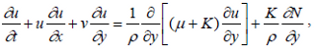	(2)
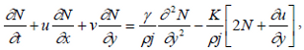	(3)
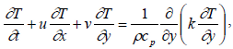	(4)

In the above equations t is the time u and v are the components of fluid velocity in the x and y directions respectively, ρ the density of ambient fluid, N the component of microrotation (angular velocity), j is the micro-inertia density, γ is the spin-gradient viscosity and T is the fluid temperature in the boundary layer region.

The boundary conditions which satisfy the above equations are as follows:

t < 0:u = v = N = 0, T = T∞ for any x, y,
t ≥ 0:u = uw (t,x), v = N = 0, T = Tw (t,x)
u → 0, N → 0, T → T∞ as y → ∞	(5a)

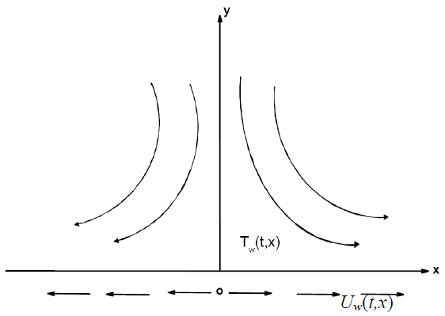
Fig. 1: Physical model and coordinate system.

We assume now that the velocity of the sheet u_w(t,x) and the sheet temperature T_w(t,x) has the following form:

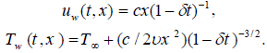(5b)

The flow is caused by the stretching of the sheet which moves in its own plane with the surface velocity u_w(t,x)=cx(1-δt)^-1, where c (stretching rate) and c are positive constants having dimension time^-1 (with 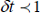, 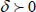which measures the unsteadiness). It is noted that the stretching rate c(1-δt)^-1 increases with time since c>0. The surface temperature of the sheet varies with the distance x from the slot and time t in the form T_w(t,x ) = T_∞ + (c/2υx²)(1 - δt)^-3/2. It should be noted that when t=0 (initial motion), Eqs. (1)-(4) describe the case of steady flow over a stretching sheet. The particular form of u_w(t,x) and T_w(t,x) presented in this paper has been chosen in order to devise a similarity transformation (Ishak et al., 2007), which transform the governing partial differential Eqs. (1)-(4) into a set of highly nonlinear ordinary differential equations.

In the present investigation, we use two semi-empirical formulae for viscosity and thermal conductivity, which introduced by Hossain and Munir (2001), as follows:

μ = μ_f (1 + (1/μ_f)(dμ/dT)_f (T - T_∞)), (6a)

and

k = k_f (1 + (1/k_f)(dk/dT)_f (T - T_∞)), (6b)

where the suffix "f" denotes the quantities outside the boundary layers.

Now we define the following dimensionless variables:

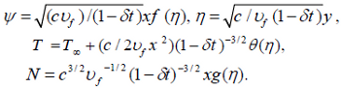(7)

where ψ is the stream function satisfying the continuity equation, f(η) is the dimensionless stream function, η is pseudo-similarity variable, g(η) is the dimensionless microrotation or angular velocity, θ(η) is the dimensionless temperature of the fluid in the boundary layer region, υ_f=μ_f /ρ is the free stream kinematic viscosity.

Substituting Eqs. (6) and (7) into Eq. (1), which is satisfied identically, and into Eqs. (2)-(5) produces the following similarity equations:

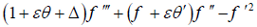	(8)
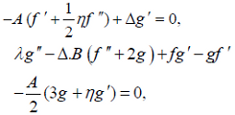	(9)
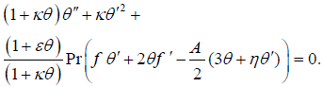	(10)

The corresponding boundary conditions transform to:

f(0) = 0, f'(0) = 1, g(0) = 0, θ(0) = 1,
f'(∞) = 0, g(∞) = θ(∞) = 0.	(11)

where ε = (1/μ_f) (d μ/dT)_f (T_w - T_∞) is the viscosity variation parameter, κ=(1/μ_f)(dk/dT)_f(T_w-T_∞) is the thermal conductivity parameter, Δ=Κ/ρυ_f is the dimensionless parameter of vortex viscosity, A=δ/c is the non-dimensional constant which measures the flow and heat transfer unsteadiness, λ=(γ/jρυ_f) is the dimensionless parameter of spin-gradient viscosity, B=(υ_f (1-δt)/jc) is the dimensionless parameter of micro-inertia density, and Pr=((1+κθ)/(1+εθ))Pr_∞ is the Prandtl number and Pr_∞=(μ_fc_f/k_f) is the is the ambient Prandtl number.

The quantities of physical interested, namely, the local skin friction C_f, the wall couple stress, m_w and the rate of heat transfer in terms of local Nusselt number Nu_x are prescribed by:

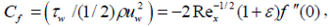	(12)
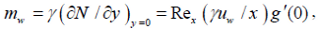	(13)
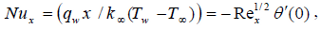	(14)

where Re_x=u_wx/υ_f is the local Reynolds number, τ_w is the skin friction and q_w is the heat transfer from the sheet are given by:

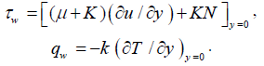(15)

III. RESULTS AND DISCUSSION

The non-linear ordinary differential Eqs. (8)-(10) subject to the boundary conditions (11) have been solved numerically by employing a shooting technique with fourth order Runge-Kutta integration scheme. Calculations were carried out for the value of the Prandtl number 1.0, the viscosity-variation parameter e ranged from 0 to 1.0, the thermal conductivity variation parameter k ranged from 0.0 to 1.0, unsteady parameter A ranged from 0.0 to 2.0 and the micropolar parameter Δ=0.0, 0.5, 1.5, are summarized with B=0.1 and λ=0.5. To verify the proper treatment of the problem, the solutions have been compared with the corresponding case of Newtonian fluid (Δ=0.0) with constant viscosity and thermal conductivity (ε=κ=0) with those cases reported by Elbashbeshy and Bazid (2004) and Sharidan et al. (2006) in Table 1 and the comparisons are found to be in a very good agreement.

Table 1. Values of skin friction coefficient -f"(0) and the heat transfer rate -θ'(0), for various values of A and Pr to the Newtonian fluid (Δ=0) with constant viscosity and thermal conductivity (ε=κ=0).

Table 2 displays the results for the values of the local skin friction coefficient as well as, Nusselt number and the wall couple stress, respectively to show the effect temperature dependent viscosity and thermal conductivity in the flow of micropolar fluids over an unsteady stretching sheet. From this table, it is observed that an increase in the value of the viscosity variation parameter ε, leads to a decrease in the value of the velocity gradient at the surface -f"(0) (the skin friction coefficient) and wall couple stress -g'(0) and hence produces an increase in the local Nusselt number, which represents the heat transfer rate at the stretching surface -θ'(0). Moreover, the effect of viscosity variation on the local skin friction coefficient and heat transfer rate is more pronounced while is less effective with wall couple stress. On other hand, it is further observed that as thermal conductivity variation parameter κ increases, there is a decrease in the local skin friction coefficient as well as the local Nusselt number and wall couple stress decrease. The increasing in κ leads to a significant difference in the values of Nusselt number but slight difference in both values of the skin friction coefficient and wall couple stress. The opposite trend is observed for the effect of unsteady parameter A, i.e. increasing A is to increase the skin friction coefficient and Nusselt number (heat transfer rate), while is less effective with a decrease in the wall couple stress. It is also observed that as micropolar parameter Δ increases for fixed values of the other parameters, both the wall couple stress and the Nusselt number increase while the skin friction coefficient decreases. As expected, the microrotation effects are more dominant near the sheet surface. In addition, the results show that the skin friction coefficient is higher in the case of Newtonian fluids (Δ=0.0) than that of micropolar fluids. This is because the micropolar fluids offer greater resistance (resulting from dynamic viscosity and vortex viscosity) to the fluid motion when compared to a Newtonian fluid.

Table 2. Values of the skin friction coefficient -f"(0), the rate of heat transfer rate -θ'(0) and the wall couple stress -g'(0), for various values of ε, κ, A and Δ, at Pr=1.0, B=0.1 and λ=0.5

Figures 2-4 display the dimensionless of velocity f'(η), microrotation g(η) and temperature θ(η) profiles for various values of the viscosity variation parameter e and the micropolar parameter Δ, respectively, while the other parameters are fixed. It is observed that the velocity and temperature across the boundary layer, increase with increasing e and microrotation or angular velocity decreases near the sheet surface but the reverse happens as one moves away from it for every value of the viscosity-variation parameter considered here. These results show that increasing the viscosity variation is to accelerate the velocity and hence produces a decrease in the temperature. Further, the boundary-layer thickness increases with an increase in e which in turn decreases the velocity gradient at the surface and wall couple stress -g'(0), while increases the rate of heat transfer -θ'(0), see, Table 2, and hence produces a decrease in the skin friction coefficient, Nusselt number. A similar behaviour was observed for the micropolar parameter Δ. As expected, the velocity and temperature inside the boundary layer increase with an increase in micropolar effects, whereas this effect is not found to be much more significant in the regime far away from the leading edge of the sheet surface. Further, it is clear that microrotation increases with increase in micropolar parameter quite effectively. Clearly the rate of change of microrotation is large for large values of micropolar parameter. Thus microconcentration is an important parameter influencing microrotation.

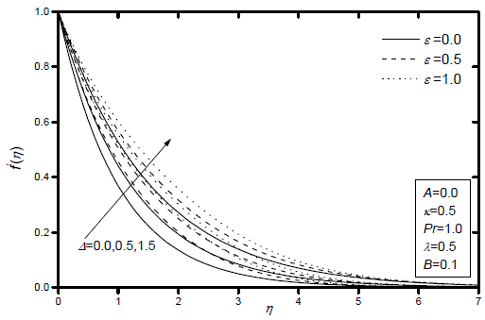
Fig. 2: Effects of the viscosity variation parameter ε and the micropolar parameter Δ on velocity profiles.

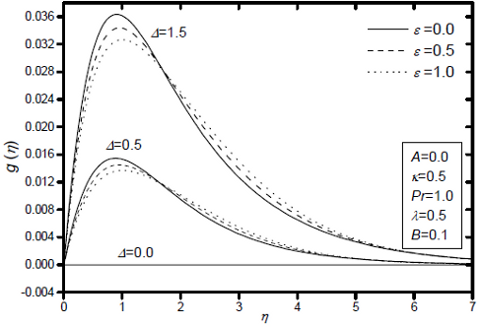
Fig. 3: Effects of the viscosity variation parameter ε and the micropolar parameter Δ on microrotation profiles.

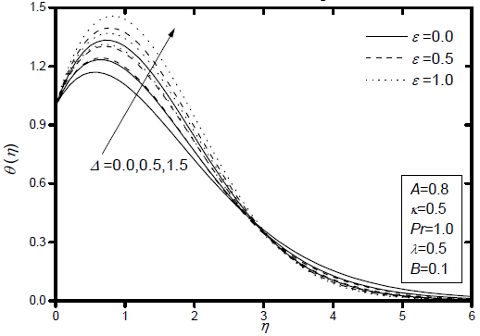
Fig. 4: Effects of the viscosity variation parameter ε and the micropolar parameter Δ on temperature profiles.

Figures 5-7 display the dimensionless of velocity f'(η), microrotation g(η) and temperature θ(η) profiles for various values of unsteady parameter A and the thermal conductivity variation parameter κ, respectively, while the other parameters are fixed. it can be seen that the velocity and temperature of the fluid increase as κ increases, while is less effective with the microrotation profiles. The opposite trend is observed for the effect of A, i.e. increasing A is to decrease the velocity, microrotation and temperature profiles, except for A=0.0. In this case A=0.0 (steady-flow case) the temperature profiles overshoot its value at the sheet surface, as can be seen from Fig.7. This behaviour is in agreement with the results of Elbashbeshy and Bazid (2004) and Sharidan et al. (2006). Moreover, the boundary-layer thickness decreases with an increase in A which in turn increases the skin friction coefficient and the Nusselt number. In addition, the effect of κ on the boundary-layer separation is not very pronounced compared to the effects of A.

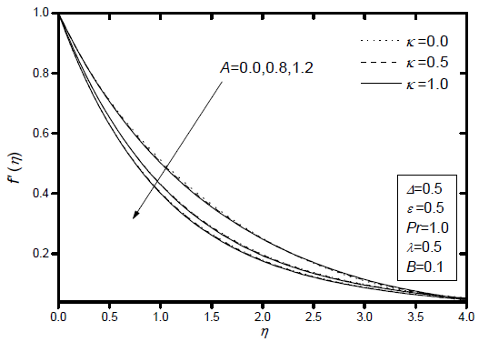
Fig. 5: Effects of the unsteady parameter A and the thermal conductivity variation parameter κ on velocity profiles.

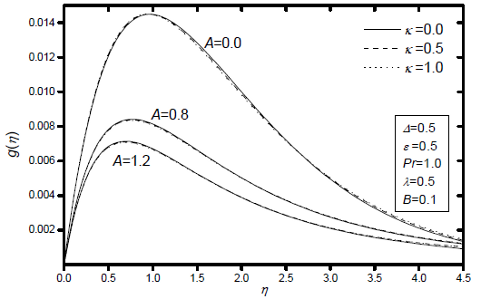
Fig. 6: Effects of the unsteady parameter A and the thermal conductivity variation parameter κ on microrotation profiles.

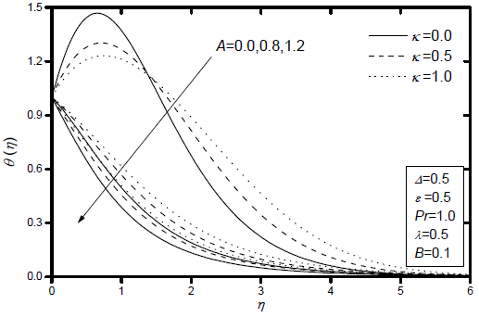
Fig. 7: Effects of the unsteady parameter A and the thermal conductivity variation parameter κ on temperature profiles.

IV. CONCLUDING REMARKS

In the present work we studied the two-dimensional laminar flow of a viscous incompressible micropolar fluid with temperature dependent viscosity and thermal conductivity over a unsteady stretching sheet. The governing equations reduced to local non-similarity boundary layer equations using suitable transformations and then solved using the Runge-Kutta numerical integration, procedure in conjunction with shooting technique. The numerical results for the velocity, microrotation and temperature profiles were illustrated graphically, while the values of the skin friction coefficient and the local Nusselt number were presented in tables, for various values of parameters. It was shown that the numericalvalues of the skin friction coefficient and the local Nus-selt number compared well with previously published results, for some particular cases of the present problem. The numerical results showed that micropolar fluids display drag reduction compared to the classical Newtonian fluids, and consequently enhanced both the heat transfer rate at the stretching surface and wall couple stress. Further, an increase in thermal conductivity variation parameter reduce the heat transfer rate. The opposite trends were observed for the effects of unsteady parameter and viscosity variation parameter on the heat transfer characteristic. Moreover, both the skin friction coefficient and the wall couple stress decreased as both the viscosity and thermal conductivity parameters increased and increasing the unsteady parameter decreased the skin friction coefficient while is less effective with the wall couple stress.

REFERENCES
1. Bhargava, R., L. Kumar and H.S. Takhar, "Mixed convection from a continuous surface in a parallel moving stream of a micropolar fluid," Heat and Mass Transfer, 39, 407-413 (2003).
2. Elbarbary, E.M.E. and N.S. Elgazery, "Chebyshev finite difference method for the effects of variable viscosity and variable thermal conductivity on heat transfer from moving surfaces with radiation," Int. J. Thermal Sciences, 43, 889-899 (2004).
3. Elbashebeshy, E.M.A. and M.A.A. Bazid, "Heat transfer over unsteady stretching surface," Heat Mass Transfer, 41, 1-4 (2004).
4. Elgazery, N.S., "The effects of chemical reaction, Hall and ion-slip currents on MHD flow with temperature dependent viscosity and thermal diffusivity," Commun. Nonlinear Sci. Num. Simul., 14, 1267-1283 (2009).
5. EL-Kabeir, S.M.M. and R.S.R. Gorla, "MHD Effects on Natural Convection in a Micropolar Fluid at a Three-Dimensional Stagnation Point in a Porous Medium," Int. J. Fluid Mechanics Research, 34, 145-158 (2007).
6. El-Kabeir, S.M.M., "Radiative effects on forced convection flows in micropolar fluids with variable viscosity," Can. J. Phys., 82, 151-165 (2004).
7. Eringen, A.C., "Simple microfluids," Int. J. Eng. Sci., 2, 205-217 (1964).
8. Gorla, R.S.R., "Unsteady mixed convection in micropolar boundary layer flow on a vertical plate," Fluid Dynam. Res., 15, 237-250(1995).
9. Hassanien, I.A., A.H. Essawy and N.M. Moursy, "Variable viscosity and thermal conductivity effects on combined heat and mass transfer in mixed convection over a UHF/UMF wedge in porous media: the entire regime," Applied Mathematics and Computation, 145, 667-682 (2003).
10. Hayat, T., Z. Abbas and T. Javed, "Mixed convection flow of a micropolar fluid over a non-linearly stretching sheet," Physics Letters A, 372, 637-647 (2008).
11. Herwing, H. and K. Gersten, "The effect of variable properties on laminar boundary layer flow," Warm Staffuberter, 20, 47-52 (1986).
12. Hossain, M.A. and M.S. Munir, "Natural convection flow of a viscous fluid about a truncated cone with temperature dependent viscosity and thermal conductivity," Int. J. Numerical Methods Heat & Fluid Flow, 11, 494-510 (2001).
13. Ishak, A., R. Nazar and I. Pop, "Boundary-layer flow of a micropolar fluid on a continuously moving or fixed permeable surface," International Journal of Heat and Mass Transfer, 50, 4743-4748 (2007).
14. Ishak, A., R. Nazar and I. Pop, "Dual solutions in mixed convection boundary layer flow of micropolar fluids," Commun. Nonlinear Sci. Num. Simul., 14, 1324-1333 (2009).
15. Kim, Y.J., "Unsteady Convection Flow of Micropolar Fluids Past a Vertical Porous Plate Embedded in a Porous Medium," Acta Mech., 148, 1-4 (2001).
16. Patil, P.M. and P.S. Kulkarni, "Effects of chemical reaction on free convective flow of a polar fluid through a porous medium in the presence of internal heat generation," Int. J. Thermal Sciences, 47, 1043-1054 (2008).
17. Rahman, M.M. and M.A. Sattar, "Magnetohydrodynamic Convective Flow of a Micropolar Fluid Past a Continuously Moving Vertical Porous Plate in the Presence of Heat Generation/Absorption," J. Heat Transfer, 128, 142-152 (2006).
18. Rahman, M.M. and M.A. Sattar, Transient convective flow of micropolar fluid past a continuously moving vertical porous plate in the presence of radiation," International Journal of Applied Mechanics and Engineering, 12, 497-513 (2007).
19. Salem, A.M., "Variable viscosity and thermal conductivity effects on MHD flow and heat transfer in viscoelastic fluid over a stretching sheet," Physics Letters A, 369, 315-322 (2007).
20. Seddeek, M.A., "Flow of a magneto-micropolar fluid past a continuously moving plate," Physics Letters A, 306, 255-257 (2003).
21. Sharidan, S., T. Mahmood and I. Pop, "Similiarity solutions for the unsteady boundary Layer flow and heat transfer due to a stretching sheet," Int. J. Applied Mechanics and Engineering, 11, 647-654 (2006).

Received: August 6, 2010.
Accepted: June 8, 2011.
Recommended by Subject Editor Walter Ambrosini.