Servicios Personalizados
Articulo
Latin American applied research
versión On-line ISSN 1851-8796
Lat. Am. appl. res. vol.43 no.2 Bahía Blanca abr. 2013
Soret effect on an unsteady free convective flow past a vertical plate in slip flow regime with periodic temperature variation
N.ahmed, H.kalita andd.kalita
Department of Mathematics, Gauhati University, Guwahati 781014, Assam,India.
saheel_nazib@yahoo.com
Abstract— An attempt has been made to study the Soret effect on an unsteady free convective flow past a vertical plate in slip-flow regime with periodic temperature variation. Analytical solution of the problem has been obtained depending on the physical parameters including the Prandtl number Pr , the Grashof number for heat transfer Gr , the Grashof number for mass transfer Gm , the Schmidt number Sc , the Soret number Soetc. The influence of these parameters on velocity field, species concentration field, temperature field, skin-friction and the rate of heat and mass transfer at the plate are discussed graphically.
Keywords— Thermal Diffusion; Slip-flow; Rarefaction; Variable Suction; Viscous Dissipation
I. INTRODUCTION
In the last few decades, much attention has been given to the theory of unsteady free convective flows that deal with temperature variation. The change in temperature causes density variation which leads to free convection current in the fluid. During the course of the day the change in atmospheric flow is caused by temperature gradients. Many researchers have carried out the study of free convection from vertical semi-infinite plates under different physical situations. In most of the investigations, the plates are assumed to be maintained at a constant temperature, which is also the temperature of the surrounding stationary fluid.
The transient free convection flow in the unsteady flow phenomena in the cooling towers is useful from practical point of view. However, in some cases free-convection flow is enhanced by superimposing oscillating temperature on the mean plate-temperature. In the initial stage of melting adjacent to a heated surface on transient heating of insulating air gapes by heat input at the start-up of furnaces, transient natural convection is of much interest.
Soundalgekar and Wavre (1977) investigated the unsteady free convection flow past an infinite vertical plate with constant suction and mass transfer. They assumed that the plate temperature oscillates in such a way that its amplitude is small. The free convection on a horizontal plate in a saturated medium with prescribed heat transfer coefficient was studied by Ramanaiah and Malarvizhi (1991). Vighnesam and Soundalgekar (1998) presented the results of the combined free and forced convection flow of water at 4ºC from a vertical plate with variable temperature. Unsteady free convection flow past a vertical porous plate was studied by Anwar (1998). The effect of a fluctuating surface temperature and concentration on natural convection flow from a vertical flat plate was given by Hossain et al (2001). The effect of variable suction on transient free convective viscous incompressible flow past a vertical plate with periodic temperature variation in a slip flow regime was studied by Sharma and Chaudhary (2003). Sharma (2005) has studied the influence of periodic temperature and concentration on unsteady free convective viscous incompressible flow and heat transfer past a vertical plate in slip flow regime.
However in the above mentioned works, the thermal diffusion (Soret) effect was not taken into account. This assumption is justified when the concentration level is very low. The flux of mass caused due to temperature gradient is known as the Soret effect or the thermal diffusion effect. The experimental investigation of the thermal diffusion effect on mass transfer related problems was first done by Charles Soret in 1879. There after this thermal diffusion is termed as the Soret effect in honour of Charles Soret. In general the Soret effect is of a smaller order of magnitude than the effect described in Fickâs law and very often it is neglected in mass transfer process. Though this effect is quite small, but the devices can be arranged to produce very steep temperature gradient so that the separation of components in mixtures is affected. Eckert and Drake (1972) have emphasized that in the cases concerning isotope separation and in mixtures between gases with very light molecular weight (H2, He) and for medium molecular weight (N2, air), Soret effect is found to be of considerable magnitude such that it can not be ignored. Following Eckert and Drake (1972) work several other investigators have carried out model studies on the Soret and Dufour effects in different heat and mass transfer problems. Some of them are Dursunkaya and Worek (1992), Kafoussias and Williams (1995), Sattar and Alam (1994), Alam et al. (2006) and Raju et al. (2008).
hmed and Kalita (2009) investigated the effect of the thermal diffusion as well as magnetic field on free convection and mass transfer flow through porous medium, taking into account the effect of a heat source. The Soret and magnetic field effects on a transient free convection flow through a porous medium bounded by a uniformly moving infinite vertical porous plate in presence of a heat source was studied by Ahmed and Kalita (2012). Ahmed and Kalita (2010) have extended their work taking into account the effect of chemical reaction on the flow and transport characteristics.
At the macroscopic level, it is accepted that the boundary condition for a viscous fluid at a solid wall is one of "no-slip". While the no-slip boundary condition has been proven experimentally to be accurate for a number of macroscopic flows, it remains an assumption that is based on physical principles. In fact, nearly two hundred years ago Navier (1823) proposed a general boundary condition that incorporates the possibility of fluid slip at a solid boundary. Navier (1823) proposed condition assumes that the fluid slip velocity at a solid surface is proportional to the shear stress at the surface. The mathematical form of the Navier (1823) proposed condition on slip velocity as emphasized by Goldstein (1965) is v=g(dv/dy) where γ being the slip coefficient, v the slip velocity and y the normal coordinate. The fluid slippage phenomemenon at solid boundaries appear in many applications such as in micro-channels or nano- channels and in applications where a thin film of light oil is attached to the moving plates or when the surface is coated with special coating such as thick monolayer of hydrophobic octdecyltrichorosilane. Due to practical applications of the fluid slippage phenomemenon at solid boundaries, several scholars have carried out their research work in that literature, the names of whom Yu and Amed (2002), Watanebe and Mizunuma (1998), Jain and Sharma (2006), Khaled and Vafai (2004) and Poonia and Chaudhary (2012) are worth mentioning.
The aim of the present work is to investigate the Soret effect on an unsteady free convective flow past a vertical plate in slip-flow regime with periodic temperature variation. This work is an extension of the work done by Jain and Sharma (2006) to take into account the effect of thermal diffusion.
II. MATHEMATICAL FORMULATION
We now consider an unsteady free convective two-dimensional flow of a viscous incompressible fluid past an infinite vertical flat porous plate in a slip-flow regime, with variable suction by making the following assumptions
| (i) | The plate is subjected to a normal periodic suction velocity. |
| (ii) | All the fluid properties except the density in the buoyancy force term are constants. |
| (iii) | The Eckert number E is small. |
| (iv) | The temperature of the plate oscillates about a non zero constant mean. |
We consider the flow in the X-direction, which is taken along the length of the plate (vertically upwards) and Y-axis is normal to it and directed into the fluid region. As the plate is of infinite length in X-direction, all the physical quantities except possibly the pressure p are assumed to be independent of  . Under these assumptions, the physical quantities are functions of
. Under these assumptions, the physical quantities are functions of 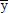 and
and 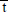 only.
only.
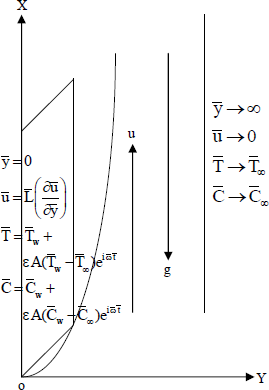
Fig 1. The flow configuration
Thecontinuity equation:
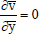 which holds for which holds for | |
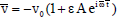 | (1) |
The Momentum Equation:
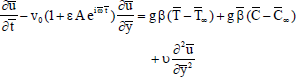 | (2) |
The energy equation:
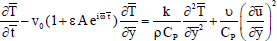 | (3) |
The species continuity equation:
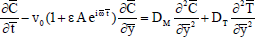 | (4) |
The relevant boundary conditions are
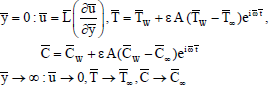 | (5) |
We now introduce the following non-dimensional quantities:
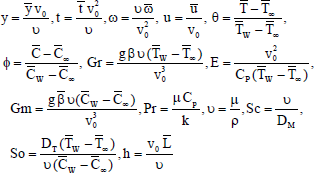 |
All the physical variables and parameters are defined in the nomenclature.
The dimensionless form of the Eqs. (2), (3) and (4) are as follows:
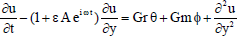 | (6) |
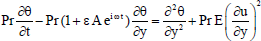 | (7) |
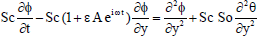 | (8) |
The boundary conditions (2-5) in non-dimensional form reduce to:
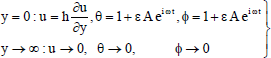 | (9) |
III.METHOD OF SOLUTION
Assuming the amplitude of oscillation εto be small, we represent the velocity u, temperature θand species concentration ϕnear the plate as
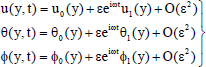 | (10) |
Substituting (10) in Eqs. (6) to (8) and equating the coefficients of ε0and ε0and neglecting those of ε2and higher powers, the following differential equations are obtained:
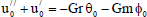 | (11) |
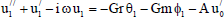 | (12) |
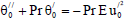 | (13) |
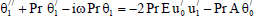 | (14) |
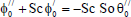 | (15) |
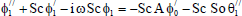 | (16) |
subject to the following boundary conditions:
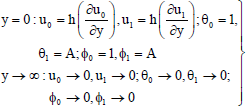 | (17) |
where dashes denote differentiation with respect to y.
The equations (11) to (16) are still coupled for the variables u0 , u1 , θ0 , θ1, ϕ0 and ϕ1
To solve them we note that E<1for all incompressible fluids and we assume that
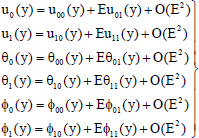 | (18) |
Substituting from (18) in Eqs. (11) to (16) and by equating the coefficients of E0and E1in each of the equations and neglecting the higher powers of E, we obtain the following second order ordinary differential equations:
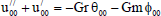 | (19) |
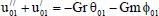 | (20) |
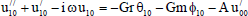 | (21) |
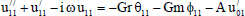 | (22) |
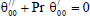 | (23) |
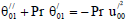 | (24) |
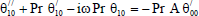 | (25) |
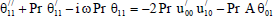 | (26) |
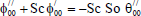 | (27) |
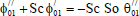 | (28) |
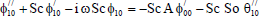 | (29) |
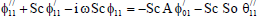 | (30) |
The boundary conditions (17) reduce to
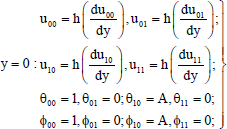 | (31) |
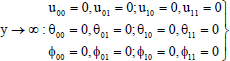 | (32) |
The solutions of the equations from (19) to (30) subject to the boundary conditions (31) and (32) are as follows
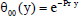 | (33) |
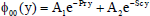 | (34) |
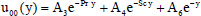 | (35) |
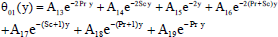 | (36) |
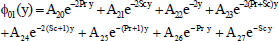 | (37) |
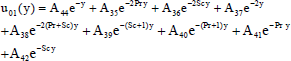 | (38) |
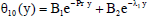 | (39) |
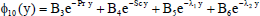 | (40) |
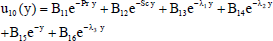 | (41) |
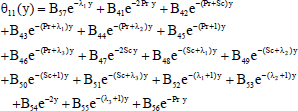 | (42) |
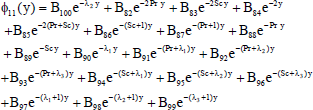 | (43) |
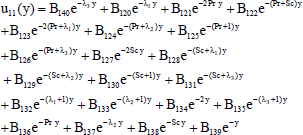 | (44) |
The constants involved in the solutions are obtained but not presented here for the sake of brevity.
Now by substituting the Eqs. (33) to (44) in Eq. (10) and splitting into real and imaginary parts and taking the real parts only, we get the expressions for the temperature, species concentration and velocity profiles as follows:
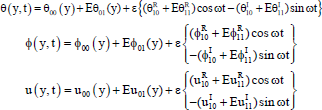 |
where
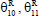 =Real part of
=Real part of 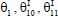 =Imaginary parto of θ1,
=Imaginary parto of θ1,
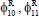 =Real part of
=Real part of 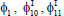 =Imaginary parto of ϕ1,
=Imaginary parto of ϕ1,
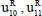 =Real part of
=Real part of 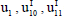 =Imaginary parto of u1
=Imaginary parto of u1
IV.COEFFICIENT OF SKIN FRICTION
The shear stress distribution is given by
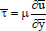 | (45) |
The skin-friction in the non-dimensional form on the plate y = 0 in the direction of free stream is given by
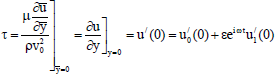 | (46) |
The Eq. (46) can be broken up into real and imaginary parts and taking the real part only, we get the skin friction τ as
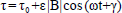 | (47) |
where
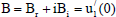 | (48) |
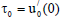 | (49) |
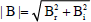 | (50) |
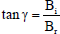 | (51) |
V.COEFFICIENT OF THE RATE OF HEAT TRANSFER
The coefficient of the rate of heat transfer (Nusselt number) between the fluid and the plate is given by
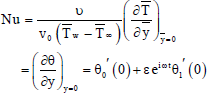 | (52) |
Splitting the Eq. (52) into real and imaginary parts and taking the real part only, we get
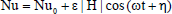 | (53) |
where
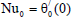 | (54) |
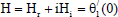 | (55) |
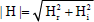 | (56) |
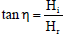 | (57) |
VI.COEFFICIENT OF MASS TRANSFER
The coefficient of the rate of mass transfer (Sherwood number) between the fluid and the plate is given by
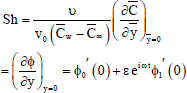 | (58) |
Splitting the equation (58) into real and imaginary parts and taking the real part only, we get
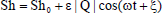 | (59) |
where
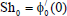 | (60) |
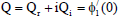 | (61) |
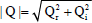 | (62) |
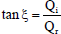 | (63) |
The expression for τ0, Nu0, Sh0, Br, Bi, Hr, Hi, Qr and Qiare obtained but not presented here for the sake of brevity.
VI.COEFFICIENT OF MASS TRANSFER
In order to discuss the effects of various parameters on the flow and transport characteristics near the plate, we have carried out numerical calculations for u,ϕ,θ,τ Nu and Sh which are respectively the non-dimensional velocity field, concentration field, temperature field, skin friction at the plate, Nusselt number at the plate and the Sherwood number at the plate for different values of So, Sc, E, h, ω and t keeping the values of Gr, Gm, A, ε fixedfixed at 10, 5, 0.2, and 0.001 respectively. The value of the Prandtl number Pris taken to be 0.7 which corresponds to the air at 20ºC. The Schmidt number Sc are taken in such a way that they represent the diffusing chemical species of common interest in air (for example Sc=0.22 for H2, Sc=0.60 for H2O, Sc=0.78 for NH3). The values of the other physical parameters are chosen arbitrarily.
The effect of Soret number So, Schmidt number Sc, Eckert number E and rarefaction parameter h on velocity u against y are presented in Figs. 2 to 5 respectively. It is seen from these figure that the velocity u increases as So, Sc, E and h are increased indicating the fact that the thermal diffusion effect or slip at the surface accelerates the fluid motion whereas the mass diffusivity causes this motion to retard. This phenomenon is consistent with the physical reality .These figures further simulate that the fluid velocity first increases in a thin layer adjacent to the plate and there after it asymptotically decreases as y increases. This is because of the effect of the buoyancy force near the plate. We also observe from these figures that u is maximum at about y = 1 and then falls for large values of y. Further we note from the figure 4 that the effect of h on u is insignificant as y → ∞.
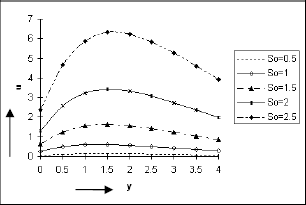
Figure 2: Velocity distribution against y for Pr=0.7, Sc=0.6, Gr=10, Gm=5, A=0.2, h=0.4, ω=1, E=0.05, ε=0.001, t=π/2.
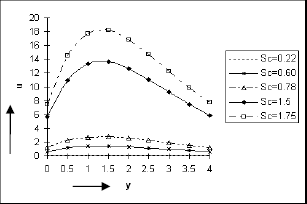
Figure 3: Velocity distribution against y for Pr=0.7, So=0.5, Gr=10, Gm=5, A=0.2, h=0.4, ω=1, E=0.05, ε=0.001, t=π/2.
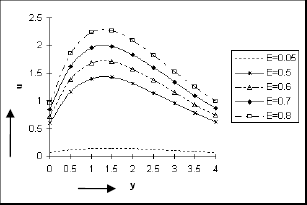
Figure 4: Velocity distribution against y for Pr=0.7, So=0.5, Sc=0.60, Gr=10, Gm=5, A=0.2, h=0.4, ω=1, ε=0.001, t=π/2.
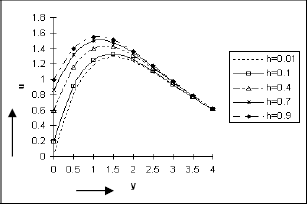
Figure 5: Velocity distribution against y for Pr=0.7, So=0.5, Sc=0.60, Gr=10, Gm=5, A=0.2, ω=1, E=0.05, ε=0.001, t=π/2.
The Figs. 6 to 9 depict the change of behaviour of species concentration ϕ against y under the effects of thermal diffusion, Schmidt number, Eckert number and rarefaction parameter respectively. Figures 6, 7 and 8 indicate that an increase in So, Sc and E causes the species concentration ϕ to increase in magnitude near the plate whereas this behaviour takes a reverse trend as we move away from the plate. It is well suppurated form the physical principles that the concentration level generally rises under the effects of thermal diffusion and frictional heat and drops due to mass diffusion. We see from figure 9 that ϕ increases in magnitude sharply for small values of increasing y, irrespective of the choice of the values of h and then ϕ again decreases in magnitude thereafter as y increases.
PARRAFO

Figure 6: Species Concentration against y for Pr=0.7, Sc=0.6, Gr=10, Gm=5, A=0.2, h=0.4, ω=1, E=0.05, ε=0.001, t=π/2.
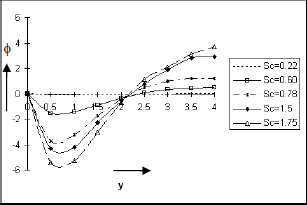
Figure 7: Species Concentration against y for Pr=0.7, So=0.5, Gr=10, Gm=5, A=0.2, h=0.4, ω=1, E=0.05, ε=0.001, t=π/2.

Figure 8: Species Concentration against y for Pr=0.7, So=0.5, Sc=0.60, Gr=10, Gm=5, A=0.2, h=0.4, ω=1, ε= 0.001, t=π/2.
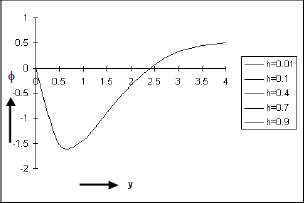
Figure 9: Species Concentration against y for Pr=0.7, So=0.5, Sc=0.60, Gr=10, Gm=5, A=0.2, E=0.05, ω=1, ε= 0.001, t=π/2.
In Figs. 10 and 11 the effects of E and h on the temperature field θ against y are shown. It is observed from Fig. 10 that the temperature θ increases as E increases and the temperature field θ increases in a thin layer adjacent to the plate and there after it decreases asymptotically as y increases. This finding has an excellent agreement to the fact that the frictional heat causes the fluid temperature to rise. The Fig. 11 indicates that the temperature field remains almost invariant under the effect of rarefaction parameter h. That is the effect of slip velocity on the temperature distribution is not countable.
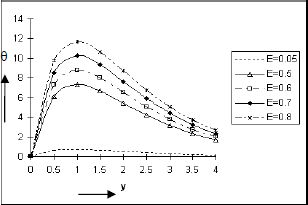
Figure 10: Temperature distribution against y for Pr=0.7, So=0.5, Sc=0.60, Gr=10, Gm=5, A=0.2, h=0.4, ω=1, ε= 0.001, t=π/2.
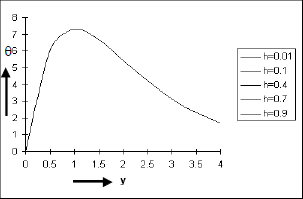
Figure 11: Temperature distribution against y for Pr=0.7, So=0.5, Sc=0.60, Gr=10, Gm=5, A=0.2, ω=1, ε= 0.001, t=π/2.
The influence of the Soret number So, Schmidt number Sc, Eckert number E and rarefaction parameter h on the skin friction τat the plate are displayed in Figs. 12 to 15. From Figs. 12, 13 and 14, it is clear that the magnitude of the skin friction τ rises when the values of the parameters So, Sc and E are increased which indicates the viscous drag on the plate increases due to thermal-diffusion, dissipative heat and increasing Schmidt number . That is the frictional resistance on the plate is lowered under mass diffusivity. Again Fig. 15 exhibits a rise in τ with a fall in h and this phenomenon is consistent with the Navier (1823) proposed condition on fluid slip. Further, we note from these figures that τ is not significantly affected by the frequency parameter ω.
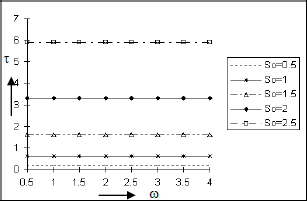
Figure 12: Skin friction at the plate y = 0 against the frequency parameter ω for Pr=0.7, Sc=0.6, Gr=10, Gm=5, A=0.2, h=0.4, E=0.05, ε=0.001, t=π/2.
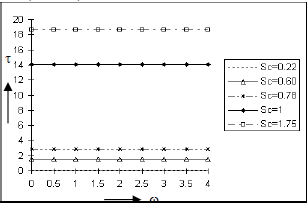
Figure 13: Skin friction at the plate y = 0 against the frequency parameter ω for Pr=0.7, So=0.5, Gr=10, Gm=5, A=0.2, h=0.4, E=0.05, ε=0.001, t=π/2.
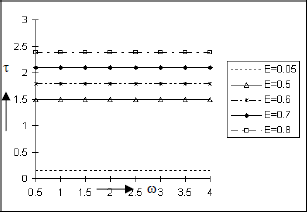
Figure 14: Skin friction at the plate y = 0 against the frequency parameter ω for Pr=0.7, So=0.5, Sc=0.6, Gr=10, Gm=5, A=0.2, h=0.4, ε= 0.001, t=π/2.
Figure 15: Skin friction at the plate y = 0 against the frequency parameter ω for Pr=0.7, So=0.5, Sc=0.06, Gr=10, Gm=5, A=0.2, E=0.05, ε=0.001, t=π/2.
Figures 16 and 17 demonstrate how the rate of heat transfer in terms of Nusselt number is affected by E and h. It is clear from Fig. 16 that |Nu| increases as E increases which indicates that the rate of heat transfer from the plate to the fluid becomes fast due to viscous dissipation of energy; whereas from Fig. 16 we notice that |Nu| increases as h decreases.
Figure 16: Nusselt Number at the plate y = 0 against the frequency parameter ω for Pr=0.7, So=0.5, Sc=0.6, Gr=10, Gm=5, A=0.2, h=0.4, ε=0.001, t=π/2.
Figure 17: Nusselt Number at the plate y = 0 against the frequency parameter ω for Pr=0.7, So=0.5, Sc=0.60, Gr=10, Gm=5, A=0.2, E=0.05, ε=0.001, t=π/2.
The Figs. 18 to 21 exhibit the nature of the Sherwood number Sh against the frequency parameter w under the effect of Soret number So, Schmidt number Sc, Eckert number E and rarefaction parameter h respectively. We see from figures 18, 19, and 20 that the coefficient of mass transfer at the plate in terms of Sherwood number Sh increases as So, Sc and E but from Fig. 21, it is clear that Sh increases as h decreases. Figures 16-21 show that heat and mass transfer are analogous processes.
Figure 18: Sherwood Number at the plate y = 0 against the frequency parameter ω for Pr=0.7, Sc=0.6, Gr=10, Gm=5, A=0.2, h=0.4, E=0.05, eε=0.001, t=pπ/2.
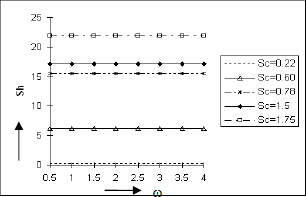
Figure 19: Sherwood Number at the plate y = 0 against the frequency parameter ω for Pr=0.7, So=0.5, Gr=10, Gm=5, A=0.2, h=0.4, E=0.05, ε=0.001, t=π/2.
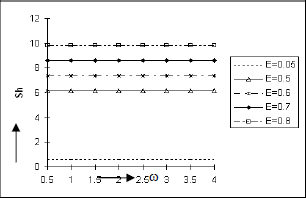
Figure 20: Sherwood Number at the plate y = 0 against the frequency parameter ω for Pr=0.7, So=0.5, Sc=0.6, Gr=10, Gm=5, A=0.2, h=0.4, ε=0.001, t=π/2.
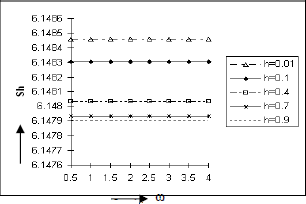
Figure 21: Sherwood Number at the plate y = 0 against the frequency parameter ω for Pr=0.7, So=0.5, Sc=0.6, Gr=10, Gm=5, A=0.2, E=0.05, ε=0.001, t=π/2.
The effect of the time t on first order velocity u1, species concentration ϕ1 and temperature field θ1 against y are presented in Figs. 22 to 24 respectively. The Fig. 22 shows that the magnitude of the first order velocity decreases as t increases in 0<t<π/2 and the direction of u1 is opposite to the direction of the buoyancy force. The same figure further indicates that there is acceleration in the upward vertical direction for the first order flow as t increases in π/2≤t≤3π/2. It is inferred from the Fig. 23 that the first order concentration level ϕ1 of the fluid rises with time for π/4≤t≤π/2 and the magnitude of ϕ1 falls as t increases in 0≤t≤π/4 near the plate. The figure 24 clearly establishes the fact that the first order temperature field θ1 drops when t is increased for 0≤t≤π/4 and |θ1|rises up with t in π/4<t≤π/3 near the plate and this behaviour takes reverse trend as we move away from the plate. It is worthwhile to mention that the zeroth order velocity or temperature or concentration is steady and so it is not influenced due to variation of time.
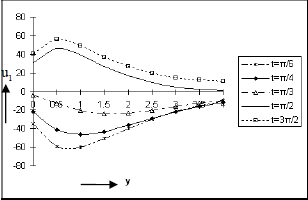
Figure 22: First order Velocity distribution against y for Pr=0.7, So=0.5, Sc=0.6, Gr=10, Gm=5, A=0.2, h=0.4, ω=1, E=0.05, ε=0.001.
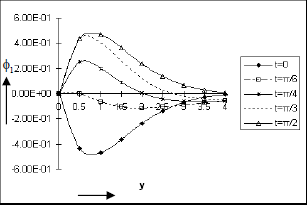
Figure 23: First order Species Concentration against y for Pr=0.7, So=0.5, Sc=0.6, Gr=10, Gm=5, A=0.2, h=0.4, ω=1, E=0.05, ε=0.001.
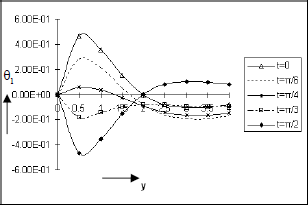
Figure 24: First order Temperature distribution against y for Pr=0.7, So=0.5, Sc=0.60, Gr=10, Gm=5, A=0.2, h=0.4, ω=1, E=0.05, ε=0.001.
VII. CONCLUSIONS
(a). The fluid velocity increases under thermal diffusion and viscous heat dissipation.
(b). The velocity slip at the plate leads to an increase in the fluid velocity.
(c). A decrease in mass diffusivity accelerates flow.
(d). The species concentration field increases in magnitude under thermal diffusion and viscous heat dissipation.
(e). A decrease chemical molecular mass diffusivity causes the magnitude of species concentration to increase.
(f). The viscous heat dissipation raises the temperature field.
(g). The magnitude of the skin friction at the plate increases under the effect of thermal diffusion and viscous heat dissipation. Further a decrease in the velocity slip causes the skin friction to increase.
(h). A decrease in chemical molecular mass diffusivity leads to an increase in the skin friction.
(i). The magnitude of heat flux at the plate rises under viscous heat dissipation and with a fall in velocity slip.
(j). The magnitude of mass flux at the plate rises under the influence of thermal diffusion and viscous heat dissipation.
(k). A fall in each of chemical molecular mass diffusivity and velocity slip leads to an increase in the magnitude of mass flux at the plate.
(l). The skin friction, heat flux and mass flux at the plate are not affected by the frequency parameter.
NOMENCLATURE
Ais the suction parameter,
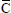 is the species concentration of the fluid,
is the species concentration of the fluid,
Cpis the specific heat at constant pressure,
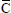 wis the species concentration of the fluid at the plate,
wis the species concentration of the fluid at the plate,
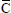 ∞is the species concentration far away from the plate,
∞is the species concentration far away from the plate,
DMis the coefficient of chemical molecular diffusivity,
DTis the coefficient of chemical thermal diffusivity,
Eis the Eckert number,
Gmis the Grashof number for mass transfer,
Gr is the Grashof number for heat transfer,
gis the acceleration due to gravity,
his the rarefaction parameter,
kis the thermal conductivity,
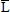 is the characteristic dimension in the flow fluid,
is the characteristic dimension in the flow fluid,
Pris the Prandtl number,
Scis the Schmidt number,
Sois the Soret number,
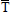 is the fluid temperature,
is the fluid temperature,
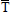 wis the temperature of the fluid at the plate,
wis the temperature of the fluid at the plate,
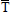 ∞is the fluid temperature far away from the plate,
∞is the fluid temperature far away from the plate,
tis the time,
uis the non dimensional fluid velocity in the boundary layer,
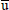 is the dimensional fluid velocity in the boundary layer,
is the dimensional fluid velocity in the boundary layer,
v0is the mean suction velocity,
yis the non dimensional distance from the plate,
βis the coefficient of volume expansion for heat transfer,
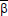 is the coefficient of volume expansion for mass transfer,
is the coefficient of volume expansion for mass transfer,
ρ is the fluid density,
µis the coefficient of viscosity,
υis the kinematic viscosity,
θis the non dimensional temperature,
ϕis the non dimensional species concentration,
ωis the frequency parameter,
εis the small reference parameter.
ACKNOWLEDGEMENT
The authors are highly grateful to UGC for supporting this work under MRP F. No. 36-96/2008(SR)
REFERENCES
1. Ahmed, N and D. Kalita, "Effect of thermal diffusion and magnetic field on an unsteady free convective flow with mass transfer through a porous medium in presence of a heat source," International J. of Math. Sci. & Eng. Appl., 3, 267-281(2009a).
2. Ahmed, N and H. Kalita, "Oscillatory MHD free convective flow through a porous medium with mass transfer, Soret effect and chemical reaction," Indian Journal of Science and Technology, 3, 929-924 (2010).
3. Ahmed, N and H. Kalita, "Soret and magnetic field effects on a transient free convection flow through a porous medium bounded by a uniformly moving infinite vertical porous plate in presence of a heat source," Int. J. of Appl. Math and Mech, 8, 1-12 (2012).
4. Alam, S., M.M. Rahman, A. Maleque and M. Ferdows, "Dufour and Soret effects on steady MHD combined free-forced convective and mass transfer flow past a semi-infinite vertical plate," Thammasat Int. J. Sci. Tech, 11, 1-12 (2006).
5. Anwar, K, "MHD unsteady free convection flow past a vertical porous plate," ZAAM, 78, 255-270 (1998).
6. Durunkya,Z. and W.M .Worek, "Diffusion-Thermo and Thermal diffusion effects in transient and steady natural convection from vertical surface," Int. J. Heat Mass Transfer, 35, 2060-2065 (1992).
7. Eckert, E.R.G. and R.M. Drake, "Analysis of Heat and Mass Transfer," Mc Grow-Hill, New York,(1972)
8. Goldstein, S., Modern Developments in Fluid Dynamics Dover, New York (1965)
9. Hossain, M.A., S. Hussain and D.A.S, Rees, "Influence of fluctuating surface temperature and concentration on natural convection flow from a vertical flat plate," ZAAM, 81, 699-709 (2001).
10. Jain, S.R. and P.K, Sharma, "Effect of viscous heating on flow past a vertical plate in slip-flow regime with periodic temperature variations," J. Rajasthan. Acad. Phy. Sci.,5,383-398 (2006).
11. Kafoussias, N.G. and E.M. Williams, "Thermal - diffusion and diffusion-Thermo effects on mixed free forced convective and mass transfer boundary layer flow with temperature dependant viscosity," Int. J. Eng. Sci., 33, 1369-1384 (1995).
12. Khaled, A.R.A. and K. Vafai, "The effect of the slip condition on Stokes and Couette flows due to an oscillating wall, exact solutions," Int. J. Nonlinear Mech., 39, 759-809 (2004).
13. Navier, C.L.M.H., Mem Acad. Sci. Inst. France,1, 414- 416 (1823).
14. Poonia, H. and R.C. Chaudhary, "The influence of radiative heat transfer on MHD oscillating flow in a planner channel with slip condition," Internationl Journal of Energy & Technology, 4, 1-7 (2012).
15. Raju, .M.C., S.V.K. Varma, P.V. Reddy and S. Saha , "Soret effects due to natural convection between heated inclined plates with magnetic field," Journal of Mechanical Engineering, 39, 65-70 (2008).
16. Ramanaiah, G. and G. Malarvizhi, "Free convection on a horizontal plate in a saturated porous medium with prescribed heat transfer coefficient," Acta Mech., 87, 73-80 (1991).
17. Sattar, M.A and M.M Alam, "Thermal diffusion as well as transpiration effects on MHD free convection and mass transfer flow past an accelerated vertical porous plate," Indian J. Pure Appl. Math., 25, 679-688 (1994).
18. Sharma, P.K, "Influence of periodic temperature and concentration on unsteady free convective viscous incompressible flow and heat transfer past a vertical plate in slip-flow regime," Mathematics: Ensenanza Universitaria XIII, 51-62 (2005).
19. Sharma, P.K. and R.C,. Chaudhary "Effect of variable suction on transient free convective viscous in compressible flow past a vertical plate with periodic temperature variable in slip flow regime," EJER, 8, 33-38 (2003).
20. Soundalgekar, V.M. and P.D.Wavre "Unsteady free convection flow past an infinite vertical plate with constant suction and mass transfer," Int. J. Heat Mass Transfer, 20, 1363-1373 (1977).
21. Vighnesam, N.V. and V.M Soundalgekar, "Combined free and forced convection flow of water at 4ºC from a vertical plate with variable temperature," Ind. J of Engineering and Material Science, 5, 124-126 (1998).
22. Watanebe, K. andY.H. Mizunuma, "Slip of Newtonian fluids at solid boundary," JSME Int. J. Ser., B41, 525-529 (1998).
23. Yu, S. and T.A. Amed, "Slip- flow heat transfer in rectangular micro channels," Int. J. Heat Mass Transfer, 44, 4225-4234 (2002).
Received: December 16, 2011
Accepted: July 23, 2012
Recommended by Subject Editor: Walter Ambrosini