Set-membership estimation theory for coupled mimo Wiener-like models

M.P. Alvarez†, L.R. Castro‡, J.L. Figueroa§ and O.E. Agamenonni*

^† Dto. de Matemática, Univ. Nac. del Sur, 8000 B. Blanca, Argentina. palvarez@criba.edu.ar
^‡ Dto. de Matemática and IIIE (UNS-CONICET), Univ. Nac. del Sur, 8000 B. Blanca, Argentina. lcastro@uns.edu.ar
^§ Dto. de Ing. Eléc. y de Comp., IIIE (UNS-CONICET), UNS, 8000 B. Blanca, Argentina. Dto. de Ing. Mecánica, Univ. Nac. del Litoral, 7500 Santa Fe, Argentina. jfigueroa@uns.edu.ar
^* Dto. de Ing. Eléc. y de Comp., CIC and IIIE (UNS-CONICET), UNS, 8000 B. Blanca, Argentina. oagamen@uns.edu.ar

Abstract — In this paper, an approach for identifying coupled multiple-input, multiple-output (MIMO) Wiener-like models is presented. Each multiple-input, single-output (MISO) model structure contained in the MIMO model is parameterized using FInite sets of discrete Laguerre transfer functions followed by High Level Canonical Piecewise Linear (HLCPWL) that represents the static memoryless nonlinear block. For each MISO model, the parameters of the HLCPWL functions are found via Set-membership (SM) estimation theory, under mild error constraints. In this way, each MISO Wiener-like model is described as a set of parameters for the nonlinear static subsystem, whose values are obtained by solving a linear programming problem. The MIMO Wiener-like model structure is then represented as a set of coupled input-output MISO models, converting the identification of a coupled MIMO system into the identification of MISO systems. In order to validate the proposed identification algorithm, an illustrative example is provided.

Keywords — Wiener Like-Models; Nonlinear Systems Identification; HLCPWL Functions; Set-Membership Estimation Theory; UBB Error.

I. INTRODUCTION

Controller design, fault detection, optimization, prediction and simulation are based on models that describe the dynamic behavior of a real system, making the identification of nonlinear dynamical systems from multiple-input, multiple-output data a very important subject.

Block-oriented models have proved useful as simple nonlinear models that describe the behavior of a great number of nonlinear dynamical systems over a large operating range. They consist of the interconnection of a linear, time-invariant dynamical block 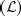and a static memoryless nonlinear block 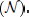One advantage of these models is that they combine a simple parametrization as well as good approximation properties. Furthermore, they require low computational effort and are suitable for controller design, making them attractive as models for control. For a complete state of the art and recent advances in this area, the reader is referred to Giri and Bai (2010).

In this work we assume that a parametric coupled MIMO system is identified using a Wiener-like structure for each MISO nominal model contained in the MIMO model. The linear dynamic part of each MISO model is represented by a finite number of Laguerre filters (álvarez et al., 2011), while the static nonlinearity is represented by HLCPWL functions (Lin et al., 1994; Julián et al., 1999).

This model has the advantage of reducing the identification of each MISO nonlinear dynamical system to two simpler steps: the identification of a linear dynamic system and the approximation of a nonlinear static function using some adequate structure.

In the literature, several approaches can be found to perform the nominal identification of block-oriented nonlinear models. Within this class, two of the most widely used model structures are the Wiener model, where 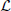precedes 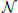(Wigren, 1993), and the Hammerstein model, where 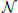is followed by 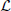(Haber and Unbehauen, 1990). These structures are present in a wide variety of fields with applications in the area of communications (Hadjiloucas et al., 2004), medicine (Celka and Colditz, 2002), biology (Hunter and Korenberg, 1986) and chemical engineering (Zhu, 1999) ; Visala et al., 1999). A detailed review of applications can be found in Janczak (2005).

Results for the Wiener models identification using different linear dynamic representation, as well as different nonlinear approximation approaches, have been presented (Billings, 1980; Castro et al., 2003; Agamennoni, 2004). The main difficulty in the identification of nonlinear block-oriented systems is that the internal signal is not available for measurement. Most of the contributions assume invertibility of the nonlinearity (Gomez and Baeyens, 2004). identification of SISO Wiener models with non-invertible nonlinearity, when the measurement errors are assumed to be unknown but bounded, have been provided in (Cerone et al., 2003; Cerone and Regruto, 2005).

This paper extends the results of álvarez et al. (2011) to MIMO dynamical systems, where the identification structure proposed for a SISO system is a Wiener-like model. In this model, the dynamic linear part is realized by using Laguerre filters and the method used for evaluating the minimum number of them is based on the Lipschitz coefficients (He and Asada, 1993). The static nonlinearity is represented by HLCPWL functions whose parameters are identified by using Set membership estimation theory, assuming that the parameters of Laguerre filters have been already identified. Furthermore, in álvarez et al. (2011) it is proved that this identification structure allows any discrete SISO nonlinear system with fading memory to be uniformly approximated. The model is nonlinear, easily identifiable from input/output (I/O) data and can predict the response of the system on arbitrarily large time horizons. These features make the actual approximation structure particularly

In order to find the optimal approximating model for a fixed number of Laguerre functions, we have to address the problem of choosing the optimal pole. In this case, we use the I/O data of the system to identify a first order ARX model, where the parameters are adjusted by using a least-squares method. The desired pole can be obtained with these parameters and this is associated to the pole of these basis functions. The reader is referred to Oliveira e Silva (2000) for some procedures to solve this problem.

The approximation of a static nonlinear function using a suitable structure requires the choice of an adequate representation that should satisfy several restrictions. First, it should allow any continuous function to be represented uniformly, and secondly it must be efficient from the point of view of the number of parameters needed to approximate a given function. Another relevant factor is the availability of a suitable algorithm for automatically adjusting the parameters. The identification of the static nonlinear functions with HLCPWL functions uses the least number of parameters and the algorithm for computing the approximation is very efficient.

In order to estimate the parameters of the HLCPWL functions, the problem is formulated within the Setmembership (SM) framework (see, e.g. Milanese (1989); Milanese and Vicino (1991) for surveys on the topic). In SM estimation theory, the uncertainty is described using an unknown but bounded additive noise, called UBB error. In this context, the estimation of the model that minimizes the worst-case identification error, is usually referred to as SM identification. In this work, the problem of estimating the parameters of the HLCPWL functions will be described in the SM identification formalism, assuming UBB error.

The paper is organized as follows. In Section II the model structure is presented. The concepts and results about HLCPWL functions and Wiener modeling are briefly summarized and the approximation structures are described. In Section III the approach for identifying the HLCPWL mapping within the framework of Set-membership estimation theory is presented and the model structure is addressed. This is the main contribution of this paper: a mechanism for MIMO Wiener-like model characterization that converts the problem of identifying the coupled MIMO dynamical system into the identification of MISO ones by applying SM theory for estimating the parameters. In Section IV an example that shows the identification capabilities of the presented structure is reported. Finally, in Section V some concluding remarks are drawn and future work is outlined.

II. MODEL STRUCTURE

In the description of block-oriented models, several approaches can be found in the literature for performing the identification process. In this article, we focus on a particular and widely-used type of block-oriented nonlinear models, the Wiener-like model, and assume it has a parametric representation.

The approach herein allows for the identification of coupled MIMO nonlinear systems to be described as the identification of a set of MISO ones.

Suppose that a Lipschitz continuous, nonlinear coupled dynamic system is excited by a sequence of multiple inputs 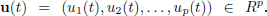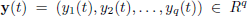are the respective outputs of the real system at each instant 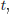being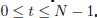

Let the pairs of input/output vectors corresponding to each SISO nonlinear dynamic system contained in the given coupled MIMO one.

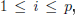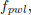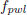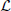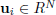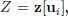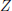Figure 1 depicts the structure used for the SISO Wiener-like model. It consists of a finite set of linear filters for each input vector u_i, followed by a nonlinear static mapping , where is a HLCPWL function. That is, the linear model maps the input vector into the intermediate signal where is a 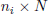matrix. The number of rows depend of the number 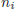of Laguerre filters used in each input vector u_i, and the overall model output is the output y_j of the nonlinear block. It is assumed that each measured output vector yj contains a UBB additive noise component e_j . Then the model structure is given by

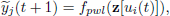(1)

for 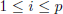and for each 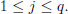The HLCPWL functions are defined on a compact domain S of the form

(2)

where 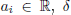is the grid size and ndiv 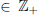is the number of divisions associated with the 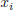axis. The domain S is partitioned by means of a simplicial boundary configuration H (Julian et al., 1999).

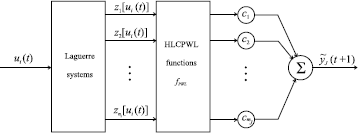
Figure 1: SISO Wiener-like model structure.

The space 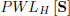of all continuous PWL mappings defined over the domain S partitioned with a simplicial boundary configuration H (Chien and Kuh, 1977), is a linear vector space. According to Julian (1999), any 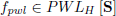can be written as

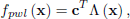(3)

where c is a vector of parameters and Λ is the matrix of the HLCPWL basis functions defined on S.

Starting from Eq. (1) we propose a model structure for the given coupled MIMO nonlinear system as a set of coupled input-output MISO ones. These are composed by the union of p finite sets of discrete-time Laguerre filters applied to each entry followed by a HLCPWL function. The output model is given by

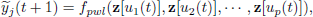(4)

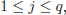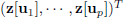for each where is a 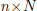matrix with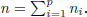

Then, from Eqs. (3) and (4) we obtain

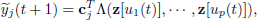(5)

where 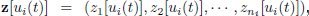for 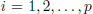are the outputs of the Laguerre filters for each input 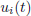and is the vector of unknown parameters of the nonlinear block which must be estimated.

In order to obtain the MISO model structure we determine the parameter cj by applying SM theory.

III. NONLINEAR MAPPING IDENTIFICATION

Assuming that

(6)

it can be easily verified that the outputs of the Laguerre filters satisfy the bound

(7)

where Therefore, the domain of the HLCPWL functions can be defined as the set

(8)

that is partitioned as described above.

Also, the input to the nonlinear mapping, i.e. the output of the linear filters, should be spread over all the simplices. Depending on the input, it is possible to have a large concentration of input/output data in a few simplices and a small number of data in most of them. To overcome this problem, we can use a simple algorithm (Castro, 2001) that removes data points from the simplices with high quantity of data points making its distribution more uniform. Besides, it guarantees the identification of all the simplices and keeps the computations easy on the number of samples.

Based on SM estimation theory (Milanese and Tempo, 1985; Kacewicz et al., 1997; Kacewicz, 1999; Garulli et al., 2000; Casini, 2004), in this section we describe the procedure for identifying the nonlinear mapping of the model.

We assume that the noise vector is UBB in 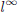norm, i.e.

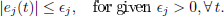(9)

We have to determine a HLCPWL function to approximate the mapping g between the Laguerre filters output and the system output 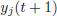related by

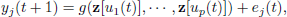(10)

for all In order to apply the SM estimation theory for finding the parameters of the HLCPWL functions, we need to define different spaces.

Let 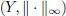the normed space of dimension N that contains the noisy measurements 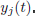The finite-dimensional normed space X is the space of unknown parameters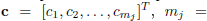 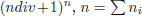is the number of Laguerre filters and ndiv is the number of cells associated with the x_i axis in Eq. (2).

According to Eq. (5), the information operator can be chosen as 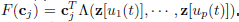Therefore, in this case 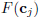is linear.

In what follows, we calculate a set estimator and the central algorithm for the estimation of the parameters c_j .

The set of Feasible Parameter Set (Casini, 2004) is defined, according to Eq. (9), as

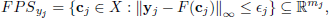(11)

and we can assure that the set FPS_yj is a convex polytope, given that 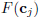is linear and the norm in the space Y is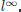

Since the set FPS_yj might have a very complex shape, great attention has been devoted to algorithms that approximate it. Most common approaches use orthotopes or ellipsoids as approximating regions. In this paper we use minimum volume outer box (MOB) and maximum volume inner box (MIB) with faces parallel to the coordinate axis.

For each k, both boxes can be computed by finding the maximum ranges of possible variations of the feasible values 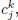, given by the values uncertainty intervals 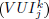defined as

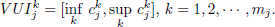(12)

The sets 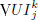give the length of each side, along the corresponding k-th coordinate axis, of the axis aligned box of minimal volume containing FPS_yj . This requires the solution of 2m_j linear programming problems with mj variables and 2N inequality constraints, for each 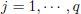as stated in the next theorem.

Theorem III.1 Let 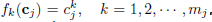For each k, the intervals 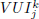can be found by solving the following linear programming problems

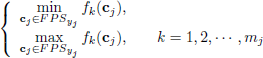(13)

subject to

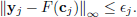(14)

Proof : The proof is immediate taking into account Eqs. (11) and (12).

To obtain the central algorithm in norm, its suffices to compute the Chebyshev center of the previously determined box, as stated in (Milanese and Tempo, 1985; Casini, 2004). The worst-case identification error is then given by the Chebyshev radius (Casini, 2004).

IV. NUMERICAL EXAMPLE

Steam Generation Unit

The process studied in this example consists of a 200 MW drum boiler. The model for this unit developed by Ray and Dutta Majumder (1983) is given by:

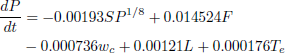(15)

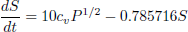(16)

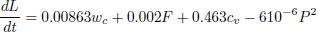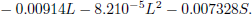	(17)

The states of the boiler's model are the drum pressure P, the steam flow to the high pressure turbine S and the drum level L. The states P and L are the controlled variables. It has two optimization variables, that are also manipulated variables: the fuel input F and the feed water input w_c, and two disturbances: the feed water temperature T_e and the control valve setting c_v. The stationary values of the state variables are presented in Table 1 1.

Henceforth we will call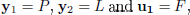

We generated a data set of 30000 samples with sampling time of 20 seconds and a random input signal was added to their nominal values. These random disturbances can take values between ±20% of the nominal value. Each value is maintained for a number of samples, in order to identify the steady-state gain. To illustrate the situation, unfavorable acquisition noise measurements are introduced, namely output data are corrupted with noise bounded by 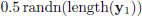and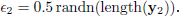

The 20000 first samples are devoted to identification and other 10000 to validation. The identification process was carried following the description given in álvarez et al. (2011). In this case, a Laguerre expansion of order 1 was selected with poles 0.95 and 0.8.

Table 1: Variables of UGVD

The nominal model fpwl was identified using estimators based on the feasible system set Eq. (11), the inputs being the outputs of the Laguerre filters. The number of identified parameters for each nonlinear structure was 9, which is equal to the number of HLCPWL functions in the representation. The estimated noise bounds were ε1 = 3.54 and ε2 = 2.71, for the available measurements y₁, y₂, respectively.

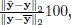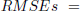
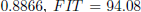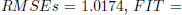
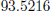For the output system y₁, the root mean square error and the FIT index, defined by attained by the model are and on the identification and validation data sets, respectively. The worst-case optimal error for the identification is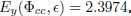

For the output system y₂, the 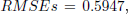on the identification data set and 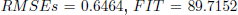on the validation data sets. The worst-case optimal error for the identification is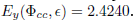

Figures 2 and 3 presents the dynamic behavior of the models 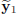and 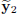compared to the system outputs y₁ and y₂.

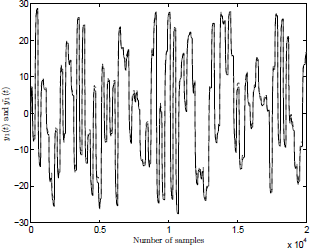
Figure 2: Laguerre-HLCPWL model. System (y1: solid line), model (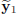: dotted line).

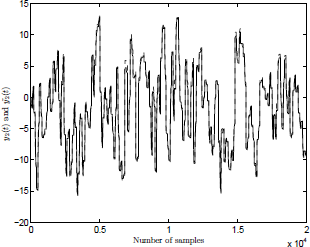
Figure 3: Laguerre-HLCPWL model. System (y2: solid line), model (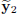: dotted line).

A validation study was performed on the validation set. In Figures 4 and 5 it can be seen that the model process mismatch is very small. It should also be noted that a first-order Laguerre model and only nine parameters for each MISO systems were used.

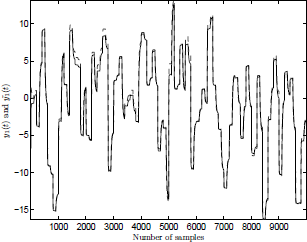
Figure 4: Laguerre-HLCPWL model on the validation set. System (y1: solid line), model (: dotted line).

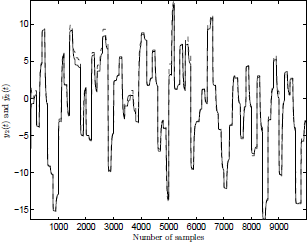
Figure 5: Laguerre-HLCPWL model on the validation set. System (y2: solid line), model (: dotted line).

V. CONCLUSIONS

A model evaluation from input-output data of a coupled MIMO nonlinear dynamic system using Setmembership estimation theory has been presented. The identified model is a Wiener-like structure, a special type of block oriented models, which is represented as a set of input-output MISO models. The linear part of each MISO model can be represented in a parametric way using rational orthonormal bases and the static nonlinearity is represented parametrically. In this work, discrete-time Laguerre filters applied to each entry ui of the dynamic system describe the main dynamic characteristics and HLCPWL functions describes the static nonlinearity.

The parameters of the HLCPWL representation were identified based on a SM approach. The advantage of this approach is that the only assumption on the noise is that it has to be bounded, in contrast with standard approaches, that rely on statistical assumptions of the noise such as stationarity, uncorrelated, etc. Estimation was stated as an optimization problem which is a linear programming one. Results show the potential of the proposed modeling technique and that a good approximation can be attained with just a few parameters. It is important to note that the HLCPWL functions have a simple electronic implementation, and thereby it is possible to develop a real-time implementation of this model structure for a large class of systems. The study of an optimal input design for the identification process within the Setmembership framework is a point of further research.

VI. ACKNOWLEDGMENTS
This work was partially supported by grants PGI 2010, SEGCyT, UNS and PICT 2010, No 1421, FONCyT, ANPCyT, Argentina

REFERENCES
1. Agammenoni, O.E., I. Skrjanc, M. Lepetic, H. Chiacchiarini and D. Matko, " Nonlinear uncertainty model of a magnetic suspension system," Math. and Computer Modelling, 40, 1075-1087 (2004).
2. Álvarez, M.P., L. R. Castro and O. E. Agamennoni, " Setmembership estimation theory for Wiener modelling using HLCPWL functions," Int. Journal on Modeling, identification and Control (IJMIC), 14(1-2), 13- 26 (2011).
3. Billings, S.A, "Identification of nonlinear systems - a survey, " IEEE Proc. Pt. D., 6, 272-284 (1980).
4. Casini, M., Set - Membership Estimation: an Advanced Tool for Systems identification, Tesis Dottorato in Ingegneria dell'Informazione, Universita degli Studi di Siena, Siena, Italy (2004).
5. Castro, L.R., O. Agamennoni and C. D'Attellis, " Identification structure using rational wavelets: Examples of application," Appl. Numerical Mathematics, 47, 345- 363 (2003).
6. Castro, L.R., Wavelets racionales en la representación de sistemas dinámicos no lineales, PhD Thesis, Depto. de Ing. Eléctrica, Universidad Nacional del Sur, Bahía Blanca, Argentina (2001).
7. Celka P. and P. Colditz, " Nonlinear nonstationary Wiener model of infart eeg seizures," IEEE Trans. Biomed. Eng., 49(6), 556-564 (2002).
8. Cerone, V., V. M. Milanese and D. Regruto, " Parameters set evaluation of Wiener models from data with bounded output errors," Proc. of the 13th IFAC Symposium on System identification, Rotterdam, the Netherlands, 849-854 (2003).
9. Cerone, V. and D. Regruto, " Set-membership identification of Wiener models with non-invertible nonlinearity, " Proc. of the 16th IFAC World Congress, Prague, Czech Republic, (2005).
10. Chien, M., and E. Kuh, " Solving nonlinear resistive networks using piecewise-linear analysis and simplicial subdivision," IEEE Trans. on Circ. and Syst., CAS- 24, 305-317 (1977).
11. Garulli, A., A. Vicino and G. Zappa, " Conditional central algorithms for worst-case set membership identification and filtering," IEEE Transactions on Automatic Control, 45(1), 14-23 (2000).
12. Giri, F. and Er-Wei Bai, Block-oriented Nonlinear System identification, Lecture Notes in Control and Information Sciences, 404, Springer-Verlag (2010).
13. Giarre, L.B. Z. Kacewicz and M. Milanese, " Model quality evaluation in set membership identification," Automatica, 33(6), 1133-1139 (1997).
14. Gómez, J.C. and E. Baeyens, " identification of blockoriented nonlinear systems using orthonormal bases," Journal of Process Control, 14, 685-697 (2004).
15. Haber, R. and H. Unbehauen, " Structure identification of nonlinear dynamic systems - a survey on input/output approaches," Automatica, 26(4), 651-677 (1990).
16. Hadjiloucas, S., A. Izhac, R. K. H. Galvao, J. W. Bowen and V. M. Becerra, " State-space model identification of a wirelessthz network," Conference Digest of the 2004 Joint 29th International Conference on Infrared and MilmeterWaves, 2004 and 12th International Conference on Terahertz Electronics, 375-376 (2004).
17. He, X and H. Asada, "A New Method for identifying Orders of input-Output Models for Nonlinear Dynamic Systems," Proc. of the ACC, 2520-2523 (1993).
18. Hunter, I.W. and M. J. Korenberg, " The identification of nonlinear biological systems: Wiener and Hammerstein cascade models," Biol. Cybern, 55(2-3), 135-144 (1986).
19. Janczak, A., Identification of nonlinear systems using neural networks and polynomial models, 310, Springer, Berlin (2005).
20. Julián, P., High Level Canonical Piecewise Linear Representation: Theory and Applications. Phd Thesis, DIEC-Universidad Nacional del Sur, Bahía Blanca, Argentina (1999).
21. Julián, P., A. Desages and O. Agamennoni, " High level canonical piecewise linear representation using a simplicial partition," IEEE Trans. on Circuits and Systems I, 46, 463-480 (1999).
22. Kacewicz, B.Z., " Worst-case conditional system identification in a general class of norms," Automatica, 35, 1049-1058 (1999).
23. Lin, J.N., H. Xu, and R. Unbehahuen, " A generalization of canonical piecewise-linear functions," IEEE Trans. on Circ. and Syst., 41, 345-347 (1994).
24. Milanese, M., Estimation theory and prediction in the presence of unknown but bounded uncertainty: A survey, Robustness in identification and control, M. Milanese, R. Tempo and A. Vicino, Eds., Plenum Press, NY (1989).
25. Milanese, M. and R. Tempo, " Optimal algorithms theory for robust estimation and prediction," IEEE Trans. on Automatic Control, 30(8), 730-738 (1985).
26. Milanese, M. and A. Vicino, " Optimal algorithms estimation theory for dynamic systems with set membership uncertainty: an overview," Automatica, 27, 997-1009 (1991).
27. Oliveira e Silva T., "Optimal Pole Conditions for Laguerre and Two-Parameter Kautz Models: A Survey of Known Results," in System identification (SYSID 2000), Ed. Smith, R., Pergamon, 2, 457-462 (2000).
28. Ray, K.S. and D. Dutta Majumder, " Simulation of a nonlinear steam generating unit," Proc. of the int. conference on systems, man and cybernetics, 1, 705 (1983).
29. Visala, A., H. Pitkaanen and J. Paanajaarvi, " Wiener nn models and robust identification," International Joint Conference on Neural Networks (IJCNN 99), Washington, DC, USA.
30. Wigren, T., " Recursive prediction error identification using the nonlinear Wiener model," Automatica, 29, 1011-1025 (1993).
31. Zhu, Y., " Distillation column identification for control using wiener model," Proc. of the American Control Conference, San Diego, CA, USA, 5, 3462-3466 (1999).

Received: May 05, 2012
Accepted: October 21, 2012
Recommended by: G. Schlotthauer & M. E. Torres