Necessary condition on the onset of double-diffusive convection in couple-stress fluid in hydromagnetics saturated by a porous medium

G.C. Rana^† and R.C. Thakur^‡

^† Department of Mathematics, NSCBM Govt. P. G. College, Hamirpur-177 005, Himachal Pradesh, INDIA E. Mail: drgcrana15@gmail.com
‡ Department of Mathematics, Govt. P. G. College, Dhaliara-177 103, Himachal Pradesh, INDIA

Abstract— In this paper, the effect of magnetic field on double-diffusive convection in couple-stress fluid saturating a porous medium is considered. By applying linear stability theory and normal mode analysis method, a necessary condition is derived which states that the viscoelastic double-diffusive convection at marginal state, cannot manifest as stationary convection if the thermal Rayleigh number R, the medium permeability parameter P_l the couple-stress parameter F, the stable solute gradient S, medium porosity e and the Chandrasekhar number Q, satisfy the inequality

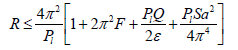
the result clearly established the stabilizing character of couple-stress parameter, stable solute gradient and magnetic field whereas destabilizing character of medium permeability and porosity.

Keywords— Couple-Stress Fluid; Double-diffusive Convection; Magnetic Field; Porous Medium.

I. INTRODUCTION

The problem of double-diffusive convection in porous media has attracted considerable interest during the last few decades, because it has various applications in geophysics, food processing, soil sciences, ground water hydrology and nuclear reactors etc. A detailed account of the thermal convection of a Newtonian fluid, under varying assumptions of hydrodynamics and hydromagnetics has been given by Chandrasekhar (1981). Lapwood (1948) has studied the convective flow in a porous medium using linearized stability theory. The Rayleigh instability of a thermal boundary layer in flow through a porous medium has been considered by Wooding (1960).

In all the above studies, the fluid is considered to be Newtonian. Although the problem of thermal convection has been extensively investigated for Newtonian fluids, relatively little attention has been devoted to this problem with non-Newtonian fluids. With the growing importance of non-Newtonian fluids with magnetic field in modern technology and industries, the investigations on such fluids are desirable. One such type of fluid is couple-stress fluid. Stokes (1966) proposed and postulated the theory of couple-stress fluid. One of the applications of couple-stress fluid is its use to the study of the mechanism of lubrication of synovial joints, which has become the object of scientific research. A human joint is a dynamically loaded bearing which has articular cartilage as the bearing and synovial fluid as lubricant. When fluid film is generated, squeeze film action is capable of providing considerable protection to the cartilage surface. The shoulder, knee, hip and ankle joints are the loaded-bearing synovial joints of human body and these joints have low-friction coefficient and negligible wear. Normal synovial fluid is clear or yellowish and is a viscous, non- Newtonian fluid.

According to the theory of Stokes (1966), couple-stresses are found to appear in noticeable magnitude in fluids. Since the long chain hylauronic acid molecules are found as additives in synovial fluid. Walicki and Walicka (1999) modeled synovial fluid as couple-stress fluid in human joints. Sharma and Thakur (2000) have studied the couple-stress fluid heated from below in hydromagnetics.

A good account of convection problems in a porous medium is given by Vafai and Hadim (2000), Ingham and Pop (1981) and Nield and Bejan (2006). Sharma and Rana (2001) have studied thermal instability of a incompressible Walters' (model B') elastico-viscous in the presence of variable gravity field and rotation in porous medium whereas stability of incompressible Rivlin-Ericksen elastico-viscous superposed fluids in the presence of uniform horizontal magnetic field in porous medium studied by Rana et al. (2011). Recently, Kumar (2011) studied stability of stratified couple-stress dusty fluid in the presence of magnetic field through porous medium whereas Rana and Sharma (2011) studied the hydromagnetic thermosolutal instability of compressible Walters' (model B') rotating fluid permeated with suspended particles in porous medium and found that magnetic field completely stabilizes the system.

Keeping in mind the importance in various applications mentioned above, our main aim in the present paper is to study the effect of magnetic field on double-diffusive convection in couple-stress elastico-viscous fluid in a porous medium.

II. MATHEMATICAL MODEL AND PERTURBATION EQUATIONS

Here, we consider an infinite, horizontal, incompressible couple-stress viscoelastic fluid of depth d, bounded by the planes z=0 and z=d in an isotropic and homogeneous medium of porosity e and permeability k₁, which is acted upon by gravity g(0,0,-g) and uniform vertical magnetic field H(0,0,H). This layer is heated and soluted from below such that a steady adverse temperature gradient β(=|dT/dz|) and a uniform solute gradient β'(=|dC/dz|) are maintained. The character of equilibrium of this initial static state is determined by supposing that the system is slightly disturbed and then following its further evolution.

Let ρ, ν, μ_c, μ_e, p, ε, T, C, α, α', H(0,0,H) and v(0, 0,0), denote respectively, the density, kinematic viscosity, couple-stress viscosity, magnetic permeability, pressure, medium porosity, temperature, concentration, thermal coefficient of expansion, solute coefficient of expansion, magnetic field and velocity of the fluid.

The equations expressing the conservation of momentum, mass, temperature, concentration and Maxwell's equations for couple-stress fluid in a porous medium (Chandrasekhar, 1981; Sharma and Thakur, 2000; Kumar, 2011) are

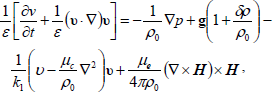	(1)
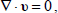	(2)
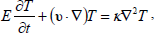	(3)
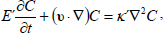	(4)
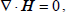	(5)
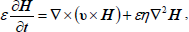	(6)

where E=ε+(1-ε) (ρ_sc_s)/(ρ₀c_f), ρ_s, c_s,, ρ₀, c_f denote the density and heat capacity of solid (porous) matrix and fluid respectively and E' is a constant analogous to E but corresponding to solute rather than heat; k, k' are the thermal diffusivity and solute diffusivity respectively.

The equation of state is

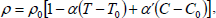(7)

where the suffix zero refers to values at the reference level z = 0.

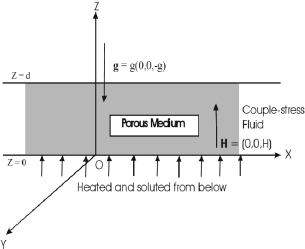
Fig. 1. Schematic sketch of physical situation

The initial state of the system is taken to be quiescent layer (no settling) with a uniform particle distribution number. The initial state is

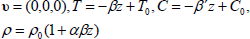(8)

is an exact solution to the governing equations.

Let v(u,v,w), θ, δp, δρ denote, respectively, the perturbations in fluid velocity v(0,0,0), temperature T, pressure p and density ρ.

The change in density dp caused by perturbation θ in temperature is given by

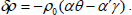(9)

The linearized perturbation equations governing the motion of fluid are

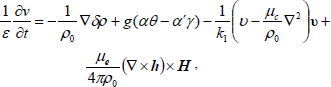	(10)
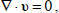	(11)
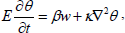	(12)
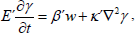	(13)
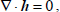	(14)
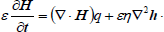	(15)

III. NORMAL MODE ANALYSIS

Following the normal mode analyses, we assume that the perturbation quantities have x, y and t dependence of the form

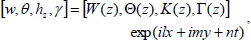(16)

where l and m are the wave numbers in the x and y directions, k=(l₂+m₂)^1/2 is the resultant wave number and n is the frequency of the harmonic disturbance, which is, in general, a complex constant.

Using expression (14) in equations (10), (12), (13) and (15) become

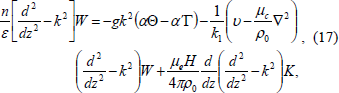	(17)
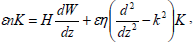	(18)
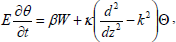	(19)
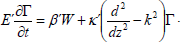	(20)

Equation (17) -(20) in non-dimensional form, become

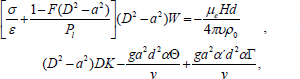	(21)
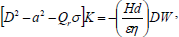	(22)
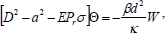	(23)
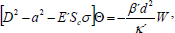	(24)

where we have put a=kd, σ=nd²/υ, and P_l= k₁/d² is the dimensionless medium permeability, P_r=υ/k is the thermal Prandtl number, Q_r=υ/h, is the magnetic Prandtl number, S_c=υ/k' is the Schmidt number, F=μ_c/(μd²) is the couple-stress parameter and D'=d (d/dz)=dD and dropping "dash" for convenience.

Substituting W=W', K=(Hd/εη)K', Θ=(βd²/k)Θ' and Γ=(β'd²/κ')Γ^* in Eqs. (21)-(24) and dropping "dash" for convenience, we obtain

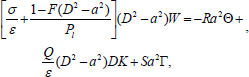	(25)
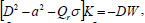	(26)
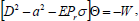	(27)
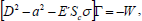	(28)

where R=gαβd⁴/(υκ) is the thermal Rayleigh number, S=gα'β'd⁴/(υκ') is the analogous solute Rayleigh number and Q=μ_eπ²d²/(4pυρ₀η) is the Chandrasekhar number.

Here we assume that the temperature at the boundaries is kept fixed, the fluid layer is confined between two boundaries and adjoining medium is electrically non-conducting. The boundary conditions appropriate to the problem are (Chandrasekhar, 1981)

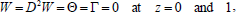(29)

and the components of h are continuous. Since the components of the magnetic field are continuous and the tangential components are zero outside the fluid, we have

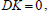(30)

on the boundaries.

Then, we prove the following theorem:

THEOREM: If R>0, F>0, Q>0 and σ=0, then the necessary condition for the existence of non-trivial solution (W,Θ,Κ,Γ) of Eqs (25)-(28) together with the boundary conditions (29) and (30) is that

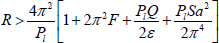
Proof: If the instability sets in stationary convection and "principle of exchange of stability" is valid, the neutral or marginal state will be characterized by σ=0 Thus the relevant governing Eqns. (21)-(23) reduces to

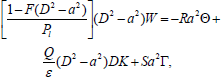	(31)
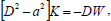	(32)
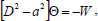	(33)
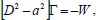	(34)

together with the boundary conditions (29) and (30).

Multiplying Eqn. (31) by W^* (the complex conjugate of W) throughout and integrating the resulting equation over the vertical range of z, we get

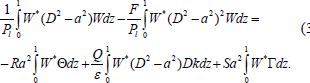(35)

Taking complex conjugate on both sides of Eqn. (33), we get

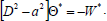(36)

Therefore,

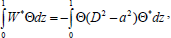(37)

Now, taking complex conjugate on both sides of Eqn. (34), we get

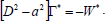(38)

Therefore,

(39)

Further,

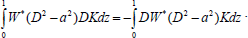(40)

Using Eqn. (32) in Eqn. (40), we get

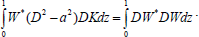(41)

Using Eqns. (37), (39) and (41) in the right hand side of Eqn. (35), we obtain

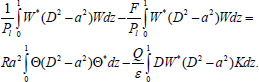(42)

Integrating term by term on both sides of Eqn. (34) for an appropriate number of times by making use of boundary conditions (24) and (25), we obtain

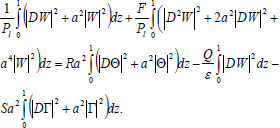(43)

Since W, K and Θ satisfy W(0)=0= W(1), Θ(0)=0=Θ(1), K(0)=0=K(1), we have by Rayleigh-Ritz inequalities

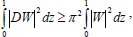	(44)
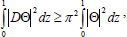	(45)
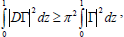	(46)

and

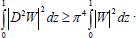(47)

Multiplying equation (33) by Θ^* (the complex conjugate of Θ), integrating by parts each term of resulting equation on the right hand side for an appropriate boundary condition, namely Θ(0)=0=Θ(1), it follows that

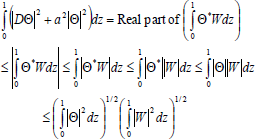(48)

(by using Cauchy-Schwartz inequality). Thus, inequalities (48) can be written as

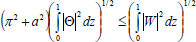(49)

Combining inequalities (36) and (37), we obtain

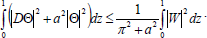(50)

Similarly, we can write

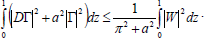(51)

Thus, if R>0, F>0, Q>0 , using the inequalities (44), (47), (50) and (51), the Eqn. (43) becomes

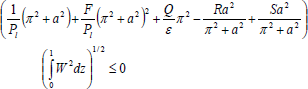(52)

Therefore, we must have

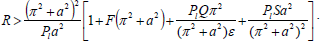
Since the minimum value of (π²+a²)²/(a²) is 4π² at a²=π²>0, hence, we necessarily have

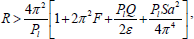(53)

which completes the proof of the theorem.

From physical point of view, the above theorem states that the onset of instability at marginal state in a couple-stress fluid heated and soluted from below in hydromagnetics saturating a porous medium cannot manifest as stationary convection, if the thermal Rayleigh number R, the couple-stress parameter F, the stable solute gradient S, the medium porosity, the medium permeability and the Chandrasekhar number Q, satisfy the inequality

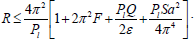(54)

IV. CONCLUSION

The effect of magnetic field on double-diffusive convection in couple-stress fluid saturating a porous medium has been investigated. From the above theorem, the main conclusions are as follows:

1. The necessary condition for the onset of instability as stationary convection for couple-stress elastico-viscous fluid is

   

2. The sufficient condition for non-existence of stationary convection at marginal state is

   

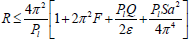
3. In the inequality (53), the thermal Rayleigh number R>0, is directly proportional to the couple-stress parameter F. Thus, couple-stress parameter has stabilizing effect on the system which is identical with the results derived by Sharma and Thakur (2000) and Kumar (2011).

4. In the inequality (53), the thermal Rayleigh number R>0, is directly proportional to the Chandrasekhar number Q, which mathematically established the stabilizing effect of magnetic field on the system as derived by Sharma and Thakur (2000), Kumar (2011) and Rana and Sharma (2011).

5. In the inequality (53), the thermal Rayleigh number R>0, is directly proportional to the stable solute gradient S, which mathematically established the stabilizing effect of stable solute gradient on the system as derived by Rana and Sharma (2011).

6. The medium permeability and porosity have destabilizing effects on the system as can be seen from inequality (53), which is an agreement with the earlier work of Sharma and Thakur (2000), Rana et al. (2011), Kumar (2011) and Rana and Sharma (2011).

REFERENCES
1. Chandrasekhar, S., Hydrodynamic and Hydromagnetic Stability, Dover Publication, New York (1981).
2. Ingham, D. and L. Pop, Transport Phenomena in Porous Media, Elsevier, New York (1981).
3. Kumar, V., "Stability of stratified couple-stress dusty fluid in the presence of magnetic field through porous medium," Appl. and Appl. Math., 6, 510-521 (2011).
4. Lapwood, E. R., "Convection of a fluid in porous medium," Proc. Camb. Phil. Soc. 44, 508-519 (1948).
5. Nield, D.A. and A. Bejan, Convection in Porous Medium, Springer, New York (2006).
6. Rana, G.C., V. Sharma and S. Kumar, "Stability of incompressible Rivlin-Ericksen elastic- iscous superposed fluids in the presence of uniform horizontal magnetic field in porous medium," J. Appl. Math. Fluid Mech., 2, 41-47 (2011).
7. Rana, G.C. and V. Sharma, "Hydromagnetic thermosolutal instability of compressible Walters' (model B') rotating fluid permeated with suspended particles in porous medium,".Int. J. of Multiphysics, 5, 325-338 (2011).
8. Sharma, R.C. and K.D. Thakur, "Couple-stress fluid heated from below in hydromagnetics," Czech. J. Phys., 50, 753-758 (2000).
9. Sharma, V. and G.C. Rana, "Thermal instability of a Walters' (model B') elastico-viscous fluid in the presence of variable gravity field and rotation in porous medium," J. Non-Equilib. Thermodyn., 26, 31-40 (2001).
10. Stokes, V.K., "Couple-stress in fluids,". Phys. Fluids, 9, 1709-1715 (1966).
11. Vafai, K. and H.A. Hadim, Hand Book of Porous Media, M. Decker, New York (2000).
12. Walicki, E. and A. Walicka "Inertial effect in the squeeze film of couple-stress fluids in biological bearings," Int. J. Appl. Mech. Engg. 4, 363-373 (1999).
13. Wooding, R.A., "Rayleigh instability of a thermal boundary layer in flow through a porous medium," J. Fluid Mech. 9, 183-192 (1960).

Received: July 19, 2012
Accepted: December 26, 2012.
Recommended by Subject Editor: Cecil Coutinho.