Servicios Personalizados
Articulo
Latin American applied research
versión On-line ISSN 1851-8796
Lat. Am. appl. res. vol.45 no.1 Bahía Blanca ene. 2015
Predictive Generalized Minimum Variance Control of Nonlinear Multivariable Systems with Non-analytical Modules
J. Wang
Jiangsu Procince Key Laboratory of Aerospace Power Systems, College of Energy & Power Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China. jiqiang.wang@nuaa.edu.cn
Abstract— For most of the control methods, it is implicitly assumed that a mathematically analytical model can be obtained before control design. This is not always feasible for many engineering systems whose analytical models are either very difficult or expensive to obtain. To handle this situation, linearization or identification techniques are usually deployed to obtain an analytical model. This paper, however, proposes a novel method to tackle directly those systems with non-analytical modules. The method does not rely on the inversion of the nonlinear system and is henceforth computationally economic. Important results are obtained on control design for nonlinear multivariable systems with non-analytical modules. Input saturation, robustness and practical implementation issues are also discussed. The proposed method is finally validated through its application to a robotic manipulator..
Keywords— Onlinear Systems; Non Analytical Modules; Nonlinear Predictive Control; Input Saturation.
I. INTRODUCTION
Nonlinear systems theory has developed rapidly over recent decades including concepts such as zero dynamics and normal forms (Isidori, 1995), passivity and dissipativity (van der Shaft, 1996), nonequilibrium theory (Byrnes, 2000), etc. As a consequence, a number of nonlinear control design techniques have been well established such as feedback linearization (Isidori, 1995), recursive designs including backstepping and forwarding (Sepulchre et al., 1997), energy-based control design for nonholonomic dynamical systems (Block et al., 2003) and nonlinear model predictive control (Mayne et al., 2000), to name just a few.
For most of control design methodologies, however, it is implicitly assumed that a mathematically analytical model can be found as expressed by differential/difference equations, or differential-algebraic equations. In many engineering systems, however, analytical expression of the system models can be very difficult or expensive to obtain. In fact, many practical systems are expressed using lookup tables or even C/Fortran codes. To handle this situation, linearization or identification techniques are used to first obtain a mathematically analytical model of the system under consideration, before any particular control design method is deployed. In this paper, however, a new approach is proposed that control design can be carried out directly based on the non-analytical models. Essentially a design framework for nonlinear multivariable systems with non-analytical modules is introduced where many specific control methods can be exercised. In this paper, a predictive control method is presented to illustrate the design framework. A brief introduction to predictive control is given in sequence.
Model Based Predictive Control (MBPC) has been very successful in industrial applications over the past three decades. The most popular predictive control algorithms are Dynamic Matrix Control (DMC) (Cutler and Ramaker, 1979; 1980) and Generalized Predictive Control (GPC) (Clarke et al., 1987a; 1987b), although almost all vendors have adopted a DMC-like approach (Qin and Badgwell, 1996; Morari and Lee, 1999). However these approaches are based on linear models and are thus inadequate to handle systems described by nonlinear models. Moreover, most systems are inherently nonlinear and this necessitates developing methods utilizing nonlinear models to achieve optimal performance over wide range of system operations.
There has been a rich history of research in the field of nonlinear model predictive control (NMPC). Many approaches have been proposed such as infinite horizon NMPC (Meadows and Rawlings, 1993) and quasi-infinite horizon NMPC (Chen and Allgöwer, 1998), contractive NMPC (De Oliveira and Morari, 2000), etc. Excellent reviews of existing NMPC techniques can be found in Mayne et al. (2000), De Nicolao et al. (2000), Rawlings (2000). Commercially available NMPC technology can be found in Qin and Badgwell (2003). Some new developments and challenges in NMPC can be referred to Magni et al. (2009) and Grüne and Pannek (2011).
One of the key questions in NMPC is closed-loop stability. As a result, most of the approaches employ a Lyapunov-based strategy where construction of Lyapunov functions for stability guarantee, e.g. via the introduction of end constraints becomes the main concern. Unlike these "stability guaranteed" approaches, the control strategy introduced here is motivated by the need to produce a control law, which is very simple to implement in industry (Grimble, 2008). In fact, many of the stability-guaranteed NMPC requiring on-line optimization are computationally expensive (De Oliveira and Morari, 2000) and there is a natural demand for a practical control law for nonlinear systems that has a sound but relatively simple theoretical basis. A promising approach is based on the generalization of an operator approach to nonlinear control, namely nonlinear generalized minimum variance control that has been developed by Grimble (Grimble, 2005; Grimble, 2008; Grimble and Pang, 2007; Grimble and Majecki, 2008). The current design method builds upon previous results on Nonlinear Generalized Minimum Variance (NGMV) control that was derived for nonlinear multivariable systems using a state space approach (Grimble, 2007; Grimble, 2008). A polynomial approach also exists as described in Grimble et al. (2007). The new development here is an extension to state space time-varying systems as well as the new feature of handling input saturation constraint and the discussion of robustness issues. The presentation of this paper is as follows: the nonlinear system model is introduced in Section 2; the criteria of determining performance index is discussed in Section 3; the optimal predictive control law is obtained in Section 4; controller properties and implementation are analyzed in Section 5; Section 6 addresses handling of input saturation while robustness issues are discussed in Section 7; Section 8 provides a case study to demonstrate the proposed design strategy and finally Section 9 concludes the work.
II. PROBLEM FORMULATION
The system model is shown in Fig. 1. The system structure is motivated by the demand to replicate the real industrial systems while producing simple results. It is assumed that the system dynamics can be separated into a nonlinear element and a linear element, possibly time-varying models with channel delays. For many industrial processes, analytical models can be very difficult or expensive to obtain. It is often the case that system dynamics are represented by lookup tables, neural networks or even a piece of C/Fortran codes, particularly for those complex nonlinear systems operating on a large envelope. It can be extremely challenging to design a control system providing good performance over the whole envelope. Needless to say most of the control theories assume that an analytical model exists before control design. Therefore it is necessitated that a control design method can be developed for handling such non-analytical systems.
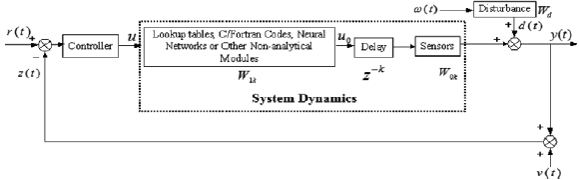
Fig. 1: Block diagram for control of general nonlinear systems.
Refer to Fig. 1, the system model is represented by a nonlinear, non-analytical module W1k, followed by the channel delay z-k with sensors dynamics W0k. The system is also affected by disturbances d(t) and measurement noise v(t). It is required to design a controller that can provide acceptable performance for such a multivariable nonlinear systems with channel delay. To proceed, the related signals are listed for easy reference.
Non-analytical module can be expressed as:
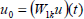 | (1) |
Linear Subsystem with Channel Delay: The linear subsystem including the channel delay is represented by the following linear time-invariant state-space model:
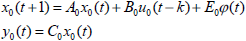 | (2) |
where ø(t), together with ω(t) that drives the disturbance model to be introduced below, is assumed to be a zero-mean white noise signal with identity covariance matrices. It should be noted that there is no loss of generality with this assumption. For example, a sensor signal can be represented as a linear system (usually a first order inertia process) driven by white noise. With this interpretation, the linear disturbance model can be readily written down in state-space form as follows:
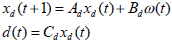 | (3) |
This disturbance model can then be combined with the above linear subsystem:
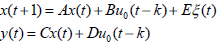 | (4) |
with: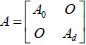 ,
, 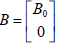 ,
, 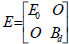 ,
, 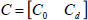 and D = D0. The vector signals are:
and D = D0. The vector signals are: 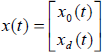 and
and 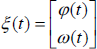 .
.
The signals shown in Fig.1 can now be listed as follows:
Error signal:
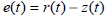 | (5) |
Plant output:
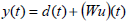 | (6) |
with
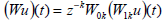 | (7) |
Observation signal:
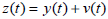 | (8) |
The future values of states and outputs can also be obtained as follows:
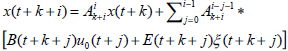 | (9a) |
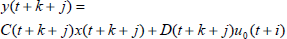 | (9b) |
where the algebra of A is defined as:
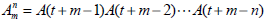 with m ≥ n and
with m ≥ n and 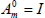 .
.
III. PERFORMANCE INDEX SELECTION
The nonlinear optimal control laws often involve the "inversion" of the nonlinear process, however, the non-analytical module in Fig. 1 may prevents such an inversion operation and consequently, a mechanism must be devised to obtain the optimal control law. The performance index is carefully chosen so that a simple control law is produced. The other criterion is that the resulting control law should recover the conventional Generalized Predictive Control (GPC) controller, when the nonlinear subsystem becomes linear. This is very important since the equivalence will provide considerable confidence in generalizing the control law to nonlinear systems.
To motivate the choice of the performance index to be minimized in the nonlinear predictive GMV framework, a brief review of the derivation of the GPC controller is provided where for the moment the input will be taken to be that for the linear time varying subsystem.
In GPC, the performance index to be minimized may be defined as:
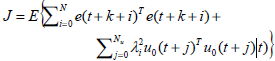 | (10) |
where 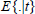 } is the conditional expectation operator, conditioned on measurements up to time t, N is the prediction horizon, k is the process delay and Nu is the control horizon. λj denotes the control signal weighting. Using the notations introduced above the performance index (10) can be rewritten as:
} is the conditional expectation operator, conditioned on measurements up to time t, N is the prediction horizon, k is the process delay and Nu is the control horizon. λj denotes the control signal weighting. Using the notations introduced above the performance index (10) can be rewritten as:
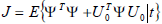 | (11) |
where 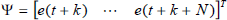 and
and 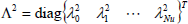 .
.
To minimize J the procedure for optimizing the deterministic signals can be utilized and this results in setting the gradient of the cost function (with respect to control U0) to zero. Then the vector of GPC control law can be shown to be:
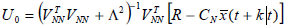 | (12) |
where the signal vectors are:
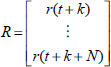 and
and 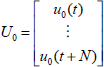 ;
;
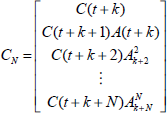 with the matrix VNN as below.
with the matrix VNN as below.
In deriving (12), the output has been assumed to be that of the combined linear model. Now (12) can be rewritten as:
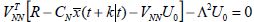 | (13) |
That is:
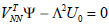 | (14) |
Consider now a new signal to be minimized involving a weighted sum of error and control input as follows:
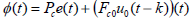 | (15) |
The vector of future values of the signal may be written as:
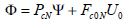 | (16) |
Comparing with (14), it is seen that if the weightings in the above equation are defined as:
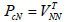 | (17) |
and
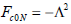 | (18) |
then minimization of the performance index (10) will be fully equivalent to the minimization of the following generalized minimum variance (GMV) type of performance index:
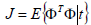 | (19) |
with  as defined in (15) and (16). This is the case since the minimization of the GMV index (19) results in setting Φ to be zero and (16) then becomes (14).
as defined in (15) and (16). This is the case since the minimization of the GMV index (19) results in setting Φ to be zero and (16) then becomes (14).
These results can be summarized as follows:
Proposition: (Connection with GPC): The minimization of the GPC performance index (10) is equivalent to the minimization of the GMV form of performance index defined by 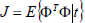 (Eq. 19) with
(Eq. 19) with 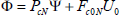 and the weightings defined by
and the weightings defined by 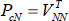 (Eq. 17) and
(Eq. 17) and 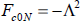 (Eq. 18).
(Eq. 18).
Proof: The proof follows easily from the above reason.
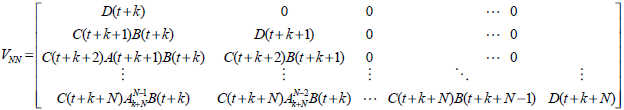 |
As a consequence of this connection, the minimization of the GMV performance index (19) will result in the same control law with GPC, if the system dynamics is linear. This provides the confidence in choosing (19) as the performance index for the nonlinear predictive GMV control problem. However from Fig. 1 it is seen that the actual input to the system is the control signal u(t), rather than the input to the linear subsystem. A new signal may then be defined including the weighting of the control signal u0 as follows:
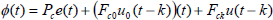 | (20) |
The vector of future values of the signal can be written as:
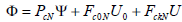 | (21) |
where:  and weightings
and weightings 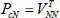 and
and 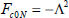 as in (17) and (18); the weighting FckN will have simple diagonal form:
as in (17) and (18); the weighting FckN will have simple diagonal form:
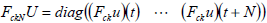 | (22) |
The performance index involves the minimization of the variance of (21) defined as follows:
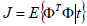 | (23) |
This performance index will be adopted as that of the nonlinear predictive GMV control problem. As having indicated in the above reasoning: if the nonlinear subsystem in Fig. 1 is absent, the control costing term FckN can be set to zero. Then the minimization of (23) is equivalent to the minimization of (10) according to Proposition 1; the resulting optimal controller then reverts to the conventional GPC controller. This is the fundamental rationale behind selecting (23) as the performance index to the nonlinear predictive GMV control problem.
IV OPTIMAL CONTROL LAW DESIGN
The optimal control law comes from setting (21) to zero:
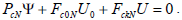 | (24) |
That is:
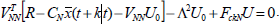 | (25) |
Since 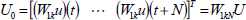 then (25) can be rewritten as:
then (25) can be rewritten as:
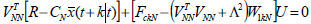 | (26) |
The optimal predicted state 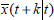 can be computed from (9) as:
can be computed from (9) as:
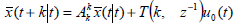 | (27) |
where 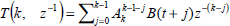 . The state
. The state 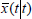 can be computed using the well-known time-varying Kalman filter (Grimble and Johnson, 1988).
can be computed using the well-known time-varying Kalman filter (Grimble and Johnson, 1988).
Inserting (27) into (26) results in the following optimality condition:
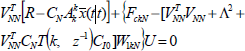 | (28) |
with 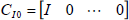 .
.
The optimal control law can then be obtained in the following two alternative forms:
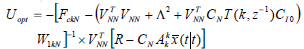 | (29) |
or
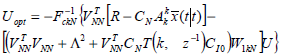 | (30) |
These important results are summarized in the following statement:
Theorem: Nonlinear Predictive GMV (NPGMV) Optimal Control Solution
Consider the nonlinear delayed multivariable system represented by Eqs. (1)-(3) as in Fig. 1, the control law that minimizes the multi-step predictive cost function
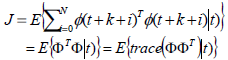 |
with 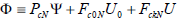 is given by:
is given by:
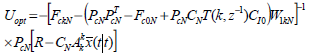 | (31) |
where 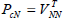 and
and 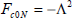 . The current control can be more conveniently obtained from the first component in the alternative expression:
. The current control can be more conveniently obtained from the first component in the alternative expression:
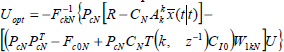 | (32) |
Proof: The proof follows from collecting the results leading to the controllers (29) and (30). Replacing 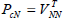 and
and 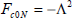 gives the desired result.
gives the desired result.
It is noted that the optimal control law (31) is of more conceptual interest and the second form of the controller (32) will be of great value for implementation. Controller implementation is discussed next.
V CONTROLLER PROPERTIES AND IMPLEMENTATION
Now invoking the receding horizon principle, the optimal control signal u(t) can be obtained by left-multiplying 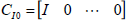 on both sides of (32):
on both sides of (32):
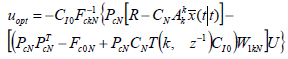 | (33) |
or
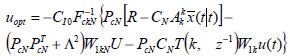 | (34) |
Decompose the symmetric matrix 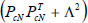 into
into 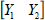 such that:
such that:
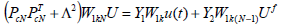 | (35) |
where Uf is the vector of future control signals and 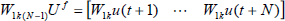 .
.
Substitute (35) into (34) the optimal control signal can now be expressed as:
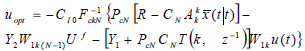 | (36) |
Noting 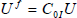 ,
, 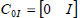 , the optimal control signal (36) can be conveniently implemented as in Fig. 2.
, the optimal control signal (36) can be conveniently implemented as in Fig. 2.
Fig. 2: Nonlinear Predictive GMV Optimal Controller Implementation with input saturation.
Remark 1: It is noted from Fig. 2 that the implementation of the optimal control signal u(t) does not rely on the inverse of the nonlinear system, thus reducing the complexity and computational burden of the controller usually associated with nonlinear controls. This provides confidence in producing a simple control law that is easy to implement in industrial applications.
VI CONSTRAINT HANDLING: INPUT SATURATION
One of the most important constraints for any control system design is the input constraint, e.g. actuators will eventually saturate. This can cause detrimental effects on system performance. The power of the NPGMV control is that it can handle the input saturation easily. This is so since the input saturation characteristic Sat(.) can be viewed as a nonlinear function of the input signal u(t). This nonlinearity can be included into the nonlinear module W1k
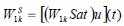 | (37) |
Then all the results derived above are valid with respect to the nonlinear subsystem 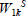 . In specific, the optimal control signal (36) holds for
. In specific, the optimal control signal (36) holds for 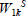 . Then the implementation scheme still applies and is clearly equivalent to simply applying the saturation characteristics to the optimal control signal u(t) as illustrated in Fig. 2. Therefore handling input saturation may only involve detuning the weighting matrices Fck. No additional controller and computational complexities are required.
. Then the implementation scheme still applies and is clearly equivalent to simply applying the saturation characteristics to the optimal control signal u(t) as illustrated in Fig. 2. Therefore handling input saturation may only involve detuning the weighting matrices Fck. No additional controller and computational complexities are required.
Remark 2: Extensive simulations have shown that the input saturation can be handled even without detuning the weighting matrices. But it should be noted that in practice, performance may deteriorate due to the fact that saturation can have changing dynamics, and this may introduce fluctuations to control signals.
VII. ROBUSTNESS ISSUES AND SMALL CONTROL
For any control system, it is important to be robust against modeling uncertainties. Comparing with mathematically analytical models, the proposed system structure regarding W1k as a non-analytical module may have the potential to be more accurate. But an analysis of the influence of a modeling error in W1k on control performance is still necessary. However, as the optimal control signal involves future predictions that are computed through W1k, and the number of computations using W1k is equal to the prediction horizon N. The analysis can be very complicated and rule-of-thumb design guidelines may be appropriate.
As the computational burden can be relieved using a small prediction horizon, e.g. N=1 is adequate. For real time applications, a small prediction horizon N and a small control weighting Fc0N=-Λ2 are applied (see the discussion below Fig. 8 in the next section). In this case, controller performance behaves similar to the following nonlinear generalized minimum variance control:
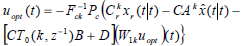 | (37) |
Fig. 8: System Performance for Varying λ: (a) q1 & control τ1 (b) q2 & control τ2.
This can be further manipulated into:
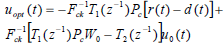 | (38) |
The above equation represents a feedback loop, and with the assumption that the nonlinear module, the linear subsystem is L-stable, an application of small gain theorem results in the claim that the system will closed-loop L-stable if the following condition is satisfied:
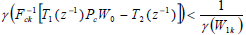 | (39) |
where γ(.) denotes the gain of the L operator.
It remains to see that a choice of small gain in 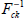 will decrease the closed-loop gain. This implies that system robustness is increased (due to small gain theorem again).
will decrease the closed-loop gain. This implies that system robustness is increased (due to small gain theorem again).
To proceed, now define 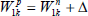 with
with 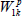 the real plant,
the real plant, 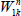 the model and Δ the additive uncertainty. The output yp now becomes:
the model and Δ the additive uncertainty. The output yp now becomes:
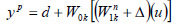 | (40) |
That is
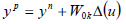 | (41) |
If Δ(u) decreases with u, then (yp-yn) will decrease for large gain in Fck. That is, a small gain in 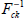 will reduce the value in (yp-yn) while enhancing the robustness.
will reduce the value in (yp-yn) while enhancing the robustness.
Remark 3: It is reasonable to assume that the system uncertainty is associated with the nonlinear module W1k while the linear subsystem Wok can be relatively accurately modeled.
Remark 4: It is seen that small gain in 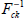 can enhance the system robustness (small gain theorem) while mitigating the detrimental effect of additive uncertainty Δ on performance. A choice of small control signal is also desirable as for practical applications, small control signal implies less energy consumption.
can enhance the system robustness (small gain theorem) while mitigating the detrimental effect of additive uncertainty Δ on performance. A choice of small control signal is also desirable as for practical applications, small control signal implies less energy consumption.
VIII. OPTIMAL PREDICTIVE CONTROL OF ROBOTIC MANIPULATOR
The optimal controller design introduced above will be illustrated in a two-link robotic manipulator shown in Fig. 3. The objective is to control the vector of joint angular positions q with the vector of torques τ applied at the manipulator joints so that they follow a desired trajectory qd.
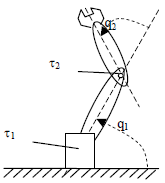
Fig. 3: Two-Link Robotic Manipulator
The dynamics of the system is highly nonlinear and can be described by the following differential equation:
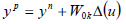 | (42) |
where H(q) is the inertia matrix, 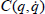 is a vector of centripetal and Coriolis torques and g(q) is a vector of torques due to gravity. For the purpose of the example, assume the manipulator is operating in the horizontal plane, and hence g(q) = 0 . A detailed system description and the numerical values for the parameters can be found in Slotine and Li (1991), where it was shown that a multi-loop PD controller could be used to move the links to required fixed positions. In this study it will be shown that a stabilizing NPGMV controller can be designed based on this PD controller and detuned to provide better performance, particularly under input saturation constraint. Effects of prediction horizon N and control weighting Δ2 are also illustrated.
is a vector of centripetal and Coriolis torques and g(q) is a vector of torques due to gravity. For the purpose of the example, assume the manipulator is operating in the horizontal plane, and hence g(q) = 0 . A detailed system description and the numerical values for the parameters can be found in Slotine and Li (1991), where it was shown that a multi-loop PD controller could be used to move the links to required fixed positions. In this study it will be shown that a stabilizing NPGMV controller can be designed based on this PD controller and detuned to provide better performance, particularly under input saturation constraint. Effects of prediction horizon N and control weighting Δ2 are also illustrated.
To proceed, the open-loop model is separated into the nonlinear and linear subsystems as shown in Fig. 4. Note that the system model is continuous and a sampling rate of Ts=2ms is adopted to discretize both the system and the PD controller. The linear subsystem states are then estimated using a Kalman filter with a unity measurement noise covariance and process disturbance covariance.
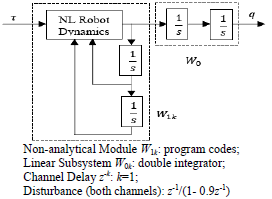
Fig. 4 Separation of Two-Link Robot Model
NPGMV Design with Input Saturation
The NPGMV controller is first designed based on the nominal stabilizing PD controller CPD(z-1): the dynamic weightings Fck is initially chosen as Fck=-CPD(z-1). The performance for N=10 and Λ2=λ×diag(1.0,0.6) with λ=0.5 is shown in Fig. 5. Also shown is the performance of the PD controller.
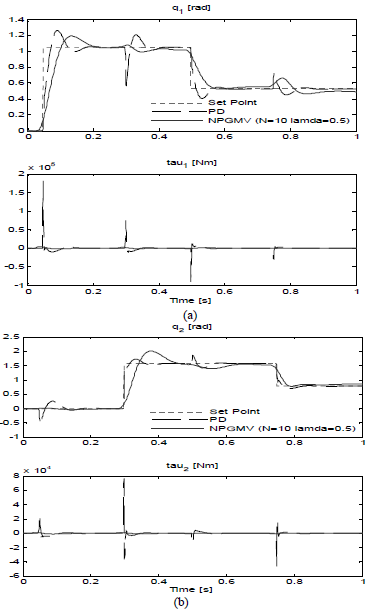
Fig. 5: Position Control of the Two-Link Robotic Manipulator: PD and NPGMV Control Designs (a) q1 & control τ1 (b) q2 & control τ2.
From Fig. 5, the NPGMV controller does not markedly improve the system performance. But it is observed that the magnitude of the control signal is much smaller than that of PD controller. The magnitude of the NPGMV control signal is in the range of [-2200, 4700] for τ1 and [-900, 1700] fo r τ2. Suppose now that due to input saturation, τ1 should be restricted in [-1700, 4000] and τ2 should be in [-600, 1500]. Then it is found that a simple detune of the NPGMV controller through decreasing the gain of the control weighting Fck achieves the above requirement, while the performance of the corresponding PD controller, with the same input constraint, deteriorates substantially. The performance of both controllers is shown in Fig. 6. It is seen that NPGMV controller handles the input saturation easily and results in much improved performance.
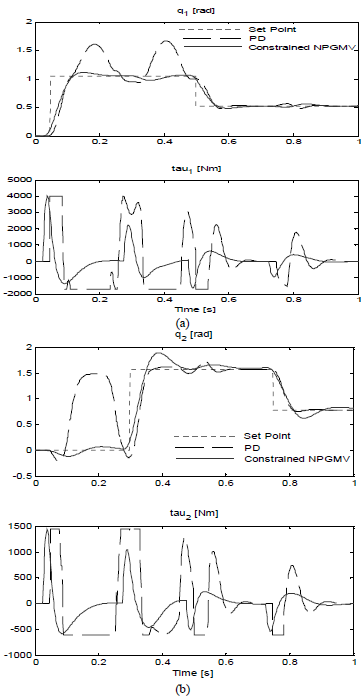
Fig. 6: PD and NPGMV Control Designs with Input Saturation: (a) q1 & control τ1 (b) q2 & control τ2.
Varying Prediction Horizon N and Weighting Λ2
The system performance for different prediction horizon (varying N) with fixed control weighting Δ2=diag(0.5,0.3) is shown in Fig. 7. Figure 8 shows the performance for different control weighting Δ2=λ×diag(1.0,0.6) (varying λ) with fixed prediction horizon N=10.
Fig. 7: System Performance for Varying N: (a) q1 & control τt1 (b) q2 & control τ2.
The results above confirm with the rule-of-thumb choice of design parameters in conventional GPC. Now recall the optimal controller implementation illustrated in Fig. 2: the future control signal involves the prediction from the nonlinear subsystem. The prediction horizon N determines the number of nonlinear subsystem blocks required for the computation of future control signal. Therefore the computational burden can be reduced significantly if the prediction horizon N is small, e.g. N=1. A short prediction horizon damps the closed loop system as seen from Fig. 7, so does a large control weighting Λ2 shown in Fig. 8. For nonlinear real time control applications, it is thus desirable to use a short prediction horizon and a small control weighting. The system performance for N=1 with varying control weighting is shown in Fig. 9. It is seen that a choice of λ=0.1 provides a good closed loop performance. It is also noted that, although not shown in Fig. 9, the PD controller destabilizes the closed loop system with the input signal magnitude saturating at the level of that for λ=0.1.
Fig. 9: System Performance for N=1 with Varying λ (Λ2=λ×diag(1.0,0.6)) λ: (a) q1 & control τ1 (b) q2 & control τ2.
Finally it should be stressed that the nonlinear predictive GMV design can be performed relatively easily and thus it will be convenient for practical implementation. In conclusion, based on a nominal stabilizing PD controller, an optimal NPGMV controller can be easily determined to improve system performance, even under the input saturation constraint. The NPGMV controller can then be detuned through either prediction horizon N or control weighting, in case additional performance is required. For real time control, a short prediction horizon N can be used and the controller can then be detuned through control weightings.
IX CONCLUSIONS
A design framework has been proposed particularly targeting those nonlinear systems with non-analytical modules. As this non-analytical module may contain lookup tables, program codes, or any other black box representations, the proposed design methodology can be applied into many engineering systems.
Another feature of the proposed method is that it does not rely on the inversion of the nonlinear process and henceforth is computationally economic. Also, the method can handle input saturation without generating additional computational burden. Although lack of stability guarantee, extensive simulations show that based on an existing PID controller, closed-loop stability can be obtained while a detuning of the weighting matrices can provide a better performance. Finally, it is worth pointing out that the proposed method handles the non-analytical systems without resorting to linearization or identification technique, therefore the work reported here should shed some light on direct control of non-analytical nonlinear systems.
Acknowledgements
This work is supported by the NUAA Fundamental Research Funds (NS2013020). The author is grateful for the fruitful discussion with Professor M.J. Grimble and Dr. R. Katebi of Industrial Control Centre, University of Strathclyde. The software support from Dr. Pawel Majecki is also greatly acknowledged.
REFERENCES
1. Block, A.M., J. Baillieul, P. Crouch and J. Marsden, Nonholonomic Mechanics and Control, Springer, (2003).
2. Byrnes, C.I., Toward a nonequilibrium theory for nonlinear control systems, Lecture Notes in Control and Information Sciences, Springer Berlin (2000).
3. Chen, H. and F. Allgöwer, "A quasi-infinite horizon non-linear model predictive control scheme with guaranteed stability," Automatica, 34, 1205-1217 (1998).
4. Clarke, D.W., C. Mohtadi and P.S. Tuffs, "Generalized predictive control-Part I: the basic algorithm," Automatica, 23, 137-148 (1987a).
5. Clarke, D.W., C. Mohtadi and P.S. Tuffs, "Generalized predictive control-Part II: extensions and interpretations," Automatica, 23, 149-160 (1987b).
6. Cutler, C.R. and B.L. Ramaker, "Dynamic matrix control-a computer control algorithm," 86th AIChE National Meeting, Houston, TX (1979).
7. Cutler, C.R. and B.L. Ramaker, "Dynamic matrix control-a computer control algorithm," Joint Automatic Control Conference, San Francisco, CA (1980).
8. De Nicolao, G., L. Magni and R. Scattolini, "Stability and robustness of nonlinear receding horizon control," In F. Allgöwer and A. Zheng (Editors), Nonlinear Predictive Control, Birkhäuser, 3-23 (2000).
9. De Oliveira, S.L. and M. Morari, "Contractive model predictive control for constrained nonlinear systems," IEEE Transactions on Automatic Control, 45, 1053-1071 (2000).
10. Grimble, M.J., "Nonlinear generalized minimum variance feedback, feedforward and tracking control," Automatica, 41, 957-969 (2005).
11. Grimble, M.J., "Why Industry Needs Improved and Practical Nonlinear Control: A Challenge for Today," IEEE Mediterranean Conference on Control and Automation, Athens, Greece, 27-29 June (2007).
12. Grimble, M.J., "Simple polynomial approach to nonlinear control," CDC Symposium to honor Bill Wolovich, Cancun, Mexico, 7 Dec. (2008).
13. Grimble, M.J. and M.A. Johnson, Optimal Multivariable Control and Estimation Theory: Theory and Applications, John Wiley, London (1988).
14. Grimble, M.J. and P. Majecki, "Nonlinear GMV control for unstable state dependent multivariable models," 47th IEEE CDC Conference, Cancun, Mexico, December (2008).
15. Grimble, M.J., P. Majecki and L. Giovanini, "Polynomial approach to nonlinear predictive GMV control," European Control Conference, Kos, Greece (2007).
16. Grimble, M.J. and Y. Pang, "NGMV control of state dependent multivariable systems," 46th IEEE CDC, 1, 1628-1633 (2007).
17. Grüne, L. and J. Pannek, Nonlinear Model Predictive Control: Theory and Algorithms, Communications and Control Engineering, Springer, London (2011).
18. Isidori, A., Nonlinear Control Systems, Springer Verlag, London (1995).
19. Magni, L., D.M. Raimondo and F. Allgower (eds), Nonlinear Model Predictive Control: Towards New Challenging Applications, Lecture Notes in Control and Information Sciences, Springer-Verlag (2009).
20. Meadows, E.S. and J.B. Rawlings, "Receding horizon control with an infinite horizon," American Control Conference, San Francisco, 2926-2930 (1993).
21. Mayne, D.Q., J.B. Rawlings, C.V. Rao and P.O.M. Scokaert, "Constrained model predictive control: stability and optimality," Automatica, 26, 789-814 (2000).
22. Morari, M. and J.H. Lee, "Model predictive control: past, present and future," Computers and Chemical Engineering, 23, 667-682 (1999).
23. Qin, S.J. and T.A. Badgwell, "An overview of industrial predictive control technology," In J.C. Kantor, C.E. Garcia, B. Carnahan, Proceedings of the 5th International Conference on chemical process control (CPC-V), Tahoe City, CA, AIChE Symposium Series No. 316, 93, 232-256 (1996).
24. Qin, S.J. and T.A. Badgwell, "A survey of industrial model predictive control technology," Control Engineering Practice, 11, 733-764 (2003).
25. Rawlings, J.B., "Tutorial overview of model predictive control," IEEE Control System Magazine, 20, 38-52 (2000).
26. Sepulchre, R., M. Jankovic and P.V. Kokotovic, Constructive Nonlinear Control, Springer-Verlag, New York (1997).
27. Slotine, J.J.E. and W. Li, Applied Nonlinear Control, Prentice Hall (1991).
28. Van der Shaft, A.J., L2 Gain and Passivity Techniques in Nonlinear Control, Springer-Verlag, Heidelberg (1996).
Received: April 17, 2013.
Accepted: August 3, 2014.
Recommended by Subject Editor: Jorge Solsona.