Servicios Personalizados
Articulo
Latin American applied research
versión On-line ISSN 1851-8796
Lat. Am. appl. res. vol.45 no.1 Bahía Blanca ene. 2015
Lubrication predictions for total knee prosthesis made of hard materials
J. Di Paolo and M.E. Berli
Grupo de Investigación en Mecánica de Fluidos, Departamento de Ingeniería Industrial
Facultad Regional Santa Fe, Universidad Tecnológica Nacional, Lavaise 610, 3000, Santa Fe, Argentina jdipaolo@bioingenieria.edu.ar
Abstract— The lubricated contact zone in a total knee prosthesis is modeled, where femoral and tibial components are supposed to be made of hard materials (high stiffness and hardness) and lubricated by a non Newtonian fluid (synovial liquid). To determine optimal relations among geometric parameters, load and film thickness, a generalized Reynolds equation was solved by means of finite element method. Although mix lubrication regime is predominant, it is shown that increasing conformity, it could be assure a full-film lubrication regime in most of the gait cycle. These results might be a reference to make more durable total knee prostheses.
Keywords— Knee Prosthesis; Lubrication; Ceramic to Ceramic Contact; Film Thickness; Finite Element Method.
I. INTRODUCTION
When the knee joint is seriously damaged and not able to move, as in the case of advanced osteoarthritis, it must be removed and replaced by total knee prosthesis. Although this is a solution for the patient, this implant has a relatively short life, up to 15 years (Berli et al., 2009), period after which it must be replaced being this a great trauma for the patient. The mechanical performance of the prosthesis is poorer than the natural knee one, being polyethylene particles liberation from wear the most frequent causes for its removal. Wear may be diminished by modifying the mechanics properties of materials, the geometry and slip velocity, characteristics that influence the generation of a lubricant film between the components of the prosthesis to avoid solid-solid contact.
In this sense, experimental a theoretical two-dimensional studies for representative knee prostheses, assuming full film lubrication of in contact compliant materials, showed that low rigidity, high viscosity and high conformity geometries, promote a lifelong of prostheses because of the reduction of wear (Mongkolwongrojn et al., 2010; McCann et al., 2009; Su et al., 2010; Pascau et al., 2009).
Alternatively to current prostheses, totally rigid prostheses are being studied in order to develop implants that could have a longer life in the body (Hutchings, 2003; Scholes et al., 2003; Udofia and Jin, 2003; Jin and Dowson, 1999). In this sense, there is more experience in hip prosthesis, for which the precision in the manufacturing process assures a high conformity between the acetabular cup and the femoral head. However, implant lifetime or premature failures have not being elucidated and they give merits for subsequent studies.
Surfaces roughness of materials used for making prostheses also influence on both wear and lubrication regime (Hutchings, 2003), being the last one of the following three kinds: full-film, mixed or boundary. As volumetric wear is inversely proportional to the hardness of materials, the use of hard materials is an alternative to reduce the worn volume (Wimmer et al., 2003; Scholes et al., 2000). Studies made with metal on metal (MOM) or ceramic on ceramic (COC) prostheses, have been inspired on the achievement of lower percentages of wear to avoid the aseptic loosening produced by polyethylene particles. On the other hand, hard materials allow obtaining smoother surfaces than soft materials (Hutchings, 2003, Di Paolo and Berli, 2006).
Additionally, an important issue for wear reduction is the lubrication regime (Udofia and Jin, 2003; Dowson et al., 2003) that in a prosthesis -as in a healthy knee- is provided by the synovial fluid; it posses non Newtonian characteristics (Bujurke et al., 2007), varying dynamically its viscosity in accordance with joint operation conditions and inducing changes on lubricant film thickness. Therefore, fluid film thickness between elements in contact is the most important parameter to be studied to assure a longer life of the implant.
The lubrication model proposed in this work is solved for the two phases of the gait cycle: stance phase and swing phase. The first is extended up to the 60% of the cycle, and is the more exigent phase, in which the supporting leg receives all the body weight and forces exerted by muscles to stabilize the joint (may act a load up to three times the body weight, see Fig. 1) (Berli et al., 2009). The remaining 40% of the cycle corresponds to the swing phase along which the joint is subjected to lower forces because the foot is not in contact with the floor, therefore joint surfaces are more separated. Although the gait cycle is a dynamic and periodic phenomenon, the frequency for normal walking is so low (one step by second) that might be studied as a succession of stationary states, where the most relevant is the instant when the load is maximum.
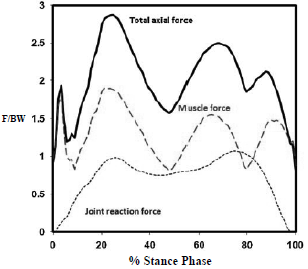
Fig. 1: Acting force (F) on the knee joint in the stance phase, expressed as a ratio of F to body weight (BW) (Extracted from Yang et al., 2010).
In this work the lubricated contact zone of a total knee prosthesis is modeled, considering the femoral and tibial components made of high stiffness materials (zero surface deformation), lubricated by non Newtonian fluid (synovial liquid). The model is solved for stance phase and swing phase separately. The aim is to determine the optimum relation among geometric factors, load and film thickness, considering that the last must be higher than the surfaces roughness.
II. METHODS
A- Equations and parameters
Figure 2 shows (out of scale) the equivalent geometry (Di Paolo and Berli, 2006) of the loaded contact, represented by a cylinder and a plane surface in longitudinal contact. This geometric approximation is often used in knee prostheses theoretical models, due to negligible curvature in the rotational axis direction. The mentioned approximation is also used in experimental models (Murakamia et al., 2000). To illustrate this idea, see Fig. 3-f from the paper by Carr and Goswami (2009). The curvature of the cylinder is the same as the original elements, which is accounted by its equivalent radius (R). Before getting the model equations, the following hypotheses are assumed: 1) Lubrication approximation; 2) non Newtonian fluid (pseudoplastic) modeled by means of power law; 3) 1D laminar and Couette dominant flow; steady state; 4) mean tangential slip velocity; 5) negligible torques on the joint; 6) negligible surface roughness; 7) constant temperature.
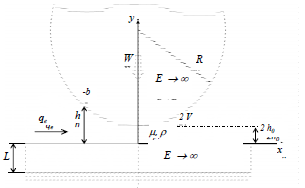
Fig. 2: Equivalent geometry of knee prosthesis made of rigid materials.
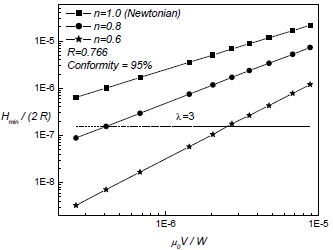
Fig. 3: Non dimensional relations for the stance phase (the load applied is three times the body weight), considering the synovial liquid both Newtonian and non Newtonian and a conformity of 95%. The value l=3 determines the limit above which the lubrication is predicted to be full-film.
The governing equations arise from mass and linear momentum conservation established on the scheme of Fig. 2. The pressure generated in the fluid, the viscosity, the flow rate and the fluid film thickness are related by the Reynolds equation, which in its integral form is:
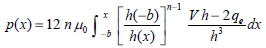 | (1) |
where p(x) is the pressure generated in the fluid, h and qe are the film thickness and flow rate respectively, m0 is a reference viscosity at the inlet position and n is the non dimensional exponent of the synovial fluid viscosity (power law) which in vivo value is unknown. However, in this work n is a parameter that varies between 0.6 and 1.0.
The boundary conditions imposed to solve equation (1) are: at the input of the flow channel the pressure is set to a reference value (zero), while Reynolds conditions are imposed at the exit, that is, the pressure and its gradient may be zero (see the paper by Di Paolo and Berli, 2006; for a detailed explanation of equation 1 and the following boundary conditions):
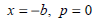 | (2) |
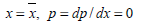 |
where 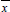 is the end of the domain and its localization is unknown. This fact turns the formulation into a free boundary problem. As non deformable surfaces are assumed, the lubrication channel geometry (film thickness) is as follows:
is the end of the domain and its localization is unknown. This fact turns the formulation into a free boundary problem. As non deformable surfaces are assumed, the lubrication channel geometry (film thickness) is as follows:
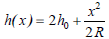 | (3) |
where 2h0 is the minimum film thickness that must be obtained for each load value (see Numerical technique).
Considering Eq. (3) and applying the boundary conditions (2) to equation (1) and to its derivatives, leads to the following equations:
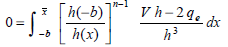 | (4) |
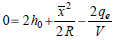 | (5) |
Finally, the load per unit width on the joint must be equilibrated by the pressure distribution, i.e.:
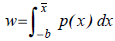 | (6) |
To assure the algorithm convergence, equations 1 to 6 are solved in dimensionless form, where the dimensional variables are scaled with the characteristic magnitudes listed in Table 1, whose values correspond to physical and operative parameters obtained from measures made on a normal knee, that are shown in Table 2. It must be noted that 1.0 Pa.s viscosity is a reference value for the definition of a characteristic pressure to obtain non-dimensional form of Reynolds equation. This value was extensively used in previous works (Di Paolo and Berli, 2006; Berli et al., 2009).
Table 1: Characteristic magnitudes for non dimensional variables definition.
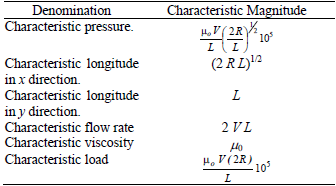
Table 2: Physical and operative parameters of a knee (Berli et al., 2009).

Under the hypothesis of steady state, the model is solved assuming parameter values corresponding to stance phase first, and then, to swing phase. The representative values for both phases are load and velocity. High loads and low velocities predominate during the stance phase, while lower loads and higher velocities predominate in the swing phase.
B- Prosthesis conformity degree
Femoral components of current knee prostheses have up to three antero-posterior curvature radii. However, only the surface corresponding to two of these radii is twined with the tibial component. The femoral component radii at the contact zone are the followings: anterior femoral radius (Rfa) and posterior femoral radius (Rfp). These two radii are calculated as a mean value among five prosthesis sizes of the same manufacturer (DePuy Products, 2004), and the conformity percentage (degree) between components is computed as follow:
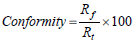 | (7) |
where Rf is the mean radius of femoral component and Rt is the tibial component radius. Anterior and posterior mean femoral radii are: Rfa=36.48 mm and Rfp=21.20 mm respectively. During normal gait, the implant works at different conformity degrees (see Blunn et al., 2003; for details). This fact justifies the simulation of stance and swing phases separately. For the first, the conformity grade between components is about 95% while for the last it is only of 55.3%. The loads on the knee for each phase of the gait cycle are listed in table 2.
C- Numerical technique
The non linear system of equations is solved by means of an algorithm based on the finite elements method with an adaptive discretization in accordance to each new position of the free boundary. Also, Newton method and parametric continuation procedures are applied.
The computational code was programmed in Computational Biomechanics Group (Di Paolo and Berli, 2006) and implemented in FORTRAN. This program computes the pressure in each node (p(x)), the minimum separation between components (hmin=2h0), the lubricant flow rate (qe) and the free boundary location  . It means that for NN selected nodes for the discretization of the solution domain, there are NN+3 unknowns. The power law exponent (n) and the load (W), are used as parameters that could be modified in the parametric continuation procedure. Equations (1), (4), (5) and (6) are used to generate the NN+3 residuals by which the unknowns are determined in a domain with 280 nodes.
. It means that for NN selected nodes for the discretization of the solution domain, there are NN+3 unknowns. The power law exponent (n) and the load (W), are used as parameters that could be modified in the parametric continuation procedure. Equations (1), (4), (5) and (6) are used to generate the NN+3 residuals by which the unknowns are determined in a domain with 280 nodes.
III. RESULTS AND DISCUSSIONS
Figures 3 and 4 show non dimensional curves in function of some relevant parameters that might be considered to make better knee prostheses from the point of view of the lubrication theory. The abscise axis shows a non dimensional parameter named specific load that relates the viscosity of reference (at the channel inlet) with the mean slip velocity and load of contact, while the non dimensional parameter on the ordinate axis relates the minimum film thickness with the equivalent cylinder radius (see Fig. 2).
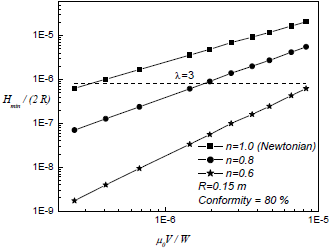
Fig. 4: Non dimensional relations for the stance phase (the load applied is three times the body weight), considering the synovial liquid both Newtonian and non Newtonian.
It can be noted that the curves in Figs. 3 and 4 are monotonic increasing functions, i.e. when joint slip velocity increases or load diminishes, the system reacts increasing the film thickness so as to generate a thicker lubrication film.
It should be convenient to consider the prediction of the lubrication regime, in terms of a set of parameters, for an optimal design. Knowing the surfaces separation (film thickness) which might be obtained by computational simulation or, in certain cases, by measures, and the mean values of surface roughness, it is possible to calculate λ, which is the ratio of the film thickness to the sum of the averaged surface roughness. Thus, λ is a useful parameter to predict the lubrication regime (Scholes et al., 2000; Scholes et al., 2003; Udofia and Jin, 2003; Dowson et al., 2003). For values of λ<<1, it will exist direct contact between surfaces, if 1<λ<3 the lubrication regime will be mixed, and if λ>3 the lubrication regime will be full-film.
It is desirable that a knee prosthesis always work in a full-film lubrication regime, where the minimum separation between surfaces must be higher than three times the averaged material roughness. Considering the equivalent radii considered in this work, the conformity degree (95% in Fig. 3 and 80 % in Fig. 4), a value of λ>3 and averaged roughness of 80 nm -corresponding to a prosthesis of CoCrMo/CoCrMo (Scholes et al., 2003)-, it is possible to plot a dashed line parallel to the abscissa axis (see Figs. 3 and 4) determining the minimum value of Hmin/(2R) above which any point will imply a full-film lubrication regime. The prosthesis being designed should have a Hmin/(2R) higher than this minimum. It can be noted from Figs. 3, 4, 5 and 6 that full-film regime in stance phase is strongly related with the operation condition (specific load) and with the conformity degree. For higher conformity degrees, is higher the possibility to obtain full-film lubrication regime, even for non Newtonian fluid. However, for the lowest values of specific load (see Fig. 5), it is observed that only Newtonian fluids might assure a full-film lubrication when conformity degree is higher than 82 %, while for higher values of specific load, full-film could be obtained for all conformity degrees explored in this work, as shown in Fig. 6.
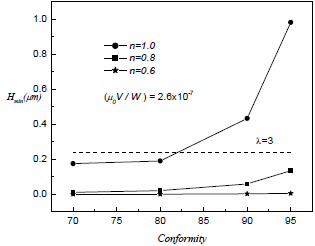
Fig. 5: Minimum film thickness in function of conformity degree for a low value of specific load. Note that full film regime could be obtained only for Newtonian fluid and conformity higher than 82%.
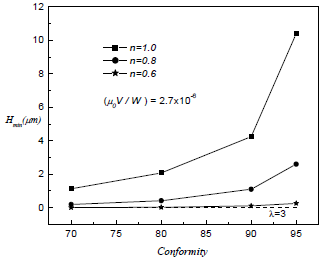
Fig. 6: Minimum film thickness in function of conformity degree for a high value of specific load. Note that full film regime could be obtained for all conformities and for Newtonian and non-Newtonian fluids.
Although there are young patients with knee pros-theses, most patients are advanced in age with high body weight and cannot move at high speed, so that the specific load falls into the lowest values of Figs. 3 and 4. The possibility to have full-film regime under low specific loads can be raised by modifying R or selecting materials that allow best surfaces finish. Depending on the material kind, the roughness might vary between 5 nm and 80nm (Scholes et al., 2003, Insley et al., 2003). Therefore, the use of alumina of third generation to make the prosthesis (because of its extreme hardness and low surfaces roughness) could assure the existence of a full-film regime in the stance phase. In this sense, the results of this work could be a guide to develop personalized prostheses.
Prostheses with several conformity degrees could be chosen for young patients. Although it was shown that high congruence grade benefits the development of a full-film lubrication regime, this might cause limitations in the joint movement, mainly at the transversal plane, leading high torques that could loosen the tibial component. Therefore, reducing the conformity degree at the anterior-posterior plane and at the same time increasing it at the medium-lateral direction (transversal), should allow obtaining an optimum conformity grade for the joint. However, this fact may be studied in detail in accordance to the biomechanics limitations of the knee and the model equations. In this sense only high conformity (higher than 95 %) degree is recommended for old patients due to their reduced capacity of moving.
In the swing phase of the gait, Fig. 7 shows that, despite the low conformity (55.3%), full-film regime is possible because of high values of specific load. These results suggest that it does not make sense in modifying significantly the conformity degree corresponding to the prosthesis working in swing phase, so that the design effort should be aimed to achieve optimal congruency for the stance phase.
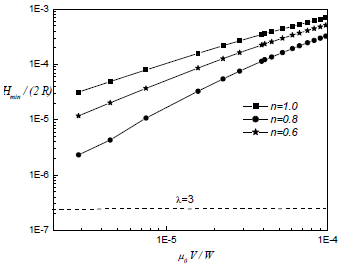
Fig. 7: Non dimensional relations for the swing phase (the load is a third of the body weight), considering the synovial liquid both Newtonian and non Newtonian.
Finally, the discussions in this work are subjected to the hypothesis of absolutely rigid elements that put it on the security side, meaning that if deformations were considered in the model, then the separation between surfaces in contact would be higher. Also, due to nanometric scale for hmin, when it reaches the range of few nanomenters (< 50) molecular forces (Van der Waals and solvatation) may be consider for more realistic predictions (Abd Al-Samieh et al., 2001; Teodorescu et al., 2006).
Finally, it must be noted that the rigid to rigid contact reduces the pressure distribution to a narrow region where a high pressure peak emerge. For situations as those shown in Fig. 5, under λ=3 line, these pressures could cause wear of surfaces in contact.
II. CONCLUSIONS
In this work, it has been shown a theoretical model of the lubrication phenomenon in a total knee prosthesis made of rigid materials. The highly nonlinear model was solved by an algorithm based on the discretization of equations by means of the finite elements method.
The minimum lubricating fluid film thickness has been obtained under steady state conditions for different slip velocities. The results show that the lubricant film thickness strongly depends not only on the geometric parameters of the prosthesis (equivalent radius and conformity degree) and specific load, but also on the material roughness and the pseudoplastic characteristic of the lubricant fluid. However, rigid materials (as metals or ceramics) could allow a lubricant film between them, reducing wear.
The results indicate that the predominant lubrication regime would be mixed lubrication. However, it could be full-film lubrication according to the conformity degree and the surface smoothness. Attending to the preceding concepts, the production of prosthesis components of high stiffness (and hardness) and low roughness is promising, in order to obtain low wear levels to minimize failure possibilities of the knee prostheses.
Future works dedicated to study the lubrication phenomenon for lower conformity degree in the stance phase, should consider the intermolecular forces that take place when the distance of surfaces in contact is in the order of few nanometers. Some calculations not presented in this work indicate a limit of 50 nm below which the influence of molecular forces must be explored.
ACKNOWLEDGEMENTS
The authors acknowledge to Universidad Tecnológica Nacional for supporting this work by the project 25/O131, which is executing at Departamento Ingeniería Industrial of Facultad Regional Santa Fe.
REFERENCES
1. Abd Al-Samieh, M.F. and H. Rahnejat, "Nano-lubricant film formation due to combined elastohydrodynamic and surface force action under isothermal conditions," Proc. Instn. Mech. Engrs., 215C, 1019-1029 (2001).
2. Berli, M., D.M. Campana, S. Ubal and J. Di Paolo, "Lubrication model of a knee prosthesis, with non newtonian fluid and porous rough material," Latin American Applied Research, 39, 105-111 (2009).
3. Blunn, G.W., C.J. Bell and P.S. Walker, "Simulator testing of total knee replacements," In: Friction, Lubrication and Wear of artificial Joints, Chapter 9, Professional Engineering Publishing, UK (2003).
4. Bujurke, N.M., B. Kudenatti Ramesh and V.B. Awati, "Efect of surface roughness on squeeze film poroelastic bearings with special reference to synovial joints," Math. Biosciences, 209, 76-89 (2007).
5. Carr, B. and T. Goswami, "Knee implants - review of models and biomechanics," Materials & Design., 30, 398-413 (2009).
6. DePuy Products, Inc. U.S., Femoral component condyle design for knee prosthesis, European Patent 0765645 (2004).
7. Di Paolo, J. and M. Berli, "Numerical análisis of the effects of material parameters on the lubrication mechanism for knee prosthesis," Computational Methods in Biomechanic and Biomedical Engineering, 9, 79-89 (2006).
8. Dowson, D., A.A.J. Goldsmith, C.M. McNie and S.L. Smith, "A tribological study of metal-on-metal total replacement hip joints," In: Friction, Lubrication and Wear of artificial Joints, Professional Engineering Publishing, UK (2003).
9. Hutchings, I.M., "Biotribology - A personal View," In: Friction, Lubrication and Wear of artificial Joints, Chapter 1, Professional Engineering Publishing, UK (2003).
10. Insley, G.M., T. Stewart, J. Nevelos, J. Fisher and R.M. Streicher, "Wear of ceramic-on-ceramic hip prosthesis under micro-separation simulation conditions," In: Friction, Lubrication and Wear of Artificial Joints, Chapter 7, Professional Engineering Publishing, UK (2003).
11. Jin, Z.M. and D. Dowson, "A Full numerical analysis of hydrodynamic lubrication in artificial hip joint replacement constructed from hard materials," Proceedings Instn Mech. Engrs., 213C, 355-370 (1999).
12. McCann, L., E. Ingham, Z. Jin and J. Fiher, "An investigation of the effect of conformity of knee hemiarthroplasty designs on contact stress, friction and degeneration of articular cartilage: a tribological study," Journal of Biomechanics, 42, 1326-1331 (2009).
13. Mongkolwongrojn, M., K. Wongseedakaew and F.E. Kennedy, "Transient elastohydrodynamic lubrication in artificial knee joint with non-Newtonian fluids," Tribology International, 43, 1017-1023 (2010).
14. Murakamia, T., Y. Sawae, K. Nakashima and J. Fisher, "Tribological Behaviour of Artificial Cartilage in Thin Film Lubrication," Tribology Series, 43, 317-327 (2000).
15. Pascau, A., B. Guardia, J.A. Puertolas and E. Gómez-Barrena, "Knee model of hydrodynamic lubrication during the gait cycle and the influence of prosthetic joint conformity," Journal of Orthopaedic Science, 14, 68-75 (2009).
16. Scholes, S.C., S.L. Smith, H.E. Ash and A. Unsworth, "The lubrication and friction of conventional UHMWPE, novel compliant layer, and hard bearing surfaces for use in total hip prosthesis," In: Friction, Lubrication and Wear of Artificial Joints, Chapter 5, Professional Engineering Publishing, UK (2003).
17. Scholes, S.C., A. Unsworth, R.M. Hall and R. Scott, "The effects of material combination and lubricant on the friction of total hip prostheses," Wear, 241, 209-213 (2000).
18. Su, Y., Z: Fu, P. Yang and C. Wang, "A full numerical analysis of elastohydrodynamic lubrication in knee prosthesis under walking condition," Journal of Mechanics in Medicine and Biology, 10, 621 (2010).
19. Teodorescu, M., S. Balakrishnan and H. Rahnejat, "Physics of ultra-thin films on molecularly smooth surfaces," Proc. IMechE Part: J.Nanoengineering and Nanosystems, 220, 7-18 (2006).
20. Udofia, I.J. and Z.M. Jin, "Elastohydrodynamic lubrication analysis of metal-on-metal hip-resurfacing prosthesis," Journal of Biomechanics, 36, 537-544 (2003).
21. Wimmer, M.A., C. Sprecher, R. Hauert, G. Täger and A. Fischer, "Tribochemical reaction on metal-on-metal hip joint bearings. A comparison between in-vitro and in-vivo results," Wear, 255, 1007-1014 (2003).
22. Yang, N.H., H. Nayeb-Hash, P.K. Canavan and A. Vaziri, "Effect of Frontal Plane Tibiofemoral Angle on the Stress and Strain at the Knee Cartilage during the Stance Phase of Gait," Journal of Orthopaedic Research, 28, 1539-1547 (2010).
Received: July 19, 2012. Received by the Subject Editor: May 15, 2014.
Accepted: August 25, 2014.
Recommended by Subject Editor: Walter Tuckart.