Servicios Personalizados
Articulo
Latin American applied research
versión On-line ISSN 1851-8796
Lat. Am. appl. res. vol.45 no.2 Bahía Blanca abr. 2015
Lie group analysis of mhd natural convection heat and mass transfer flow of a casson fluid over an inclined surface with chemical reaction
A. Mahdy
Mathematics Department, Faculty of Science, South Valley University, Qena, Egypt. mahdy@svu.edu.eg
Abstract — Natural convective heat and mass transfer of a non-Newtonian fluid over an inclined surface with uniform magnetic field and chemical reaction has been investigated numerically. The Casson fluid model is used to characterize the non-Newtonian fluid behavior and the first order of chemical reaction is considered. Lie group analysis is employed to obtain the symmetries of the governing system of partial differential equations and they reduce them to a system of ordinary differential equations via scaling transformation. Numerical computations have been carried out using the fourth order Runge-Kutta scheme with shooting techniques with a systematic guessing values of F1'(0), F3' and F4'(0). The procedure is repeated until we get the results up to the desired degree of accuracy, namely 10-5 .
Keywords — Lie Group; Casson Fluid; Chemical Reaction; MHD; Inclined Surface.
I. INTRODUCTION
Lie group analysis is a systematic way of finding the invariant or self-similar solutions of a system of partial differential equations. The method is capable of providing a deep insight into the underlying physical problems-described by partial differential equations. The applications of Lie group analysis are twofold: Producing a new solution from an existing solution or finding similarity solution of partial differential equation. The focus in the present paper is on the latter type of the application. Starting from the Sophus Lie (1842-1899), this technique is extensively used for finding solution of differential equations (Olver 1986; Bluman and Kumei 1989; Ibragimov 1994). Jalil et al. (2010) applied this method to find possible similarity transformation for the mixed convection flow over a stretching surface. They extended their work to flow of non- Newtonian fluids (Jalil et al., 2013; Jalil and Asghar, 2013), by finding self similar solution of the governing equations, using Lie group analysis. Hamad et al. (2012) investigated the combined effects of heat and mass transfer by Lie group analysis over a moving surface. Bhuvaneswari et al. (2009) and Ferdows et al. (2013a) applied the method of one parameter continuous group theory to investigate mixed convection over horizontal moving porous flat plate. Recently, Ferdows et al. (2013b) used a special form of Lie group of transformation (scaling transformation) to study the convective effects of heat and mass transfer over a radiating stretching sheet.
The mass transfer problems have great importance in extending the theory of separation processes and chemical kinetics. Processes involving the effects of mass transfer have attracted the attention of researchers due to its applications in many engineering applications, such as chemical processing equipments. The driving force for mass transfer is the difference in concentration.
The effects of chemically reactive species on fluid flow due to a stretching sheet bear equal importance in engineering research. The diffusion of a chemically reactive species in a laminar boundary layer flow over a flat plate was studied by Chambre and Young (1958). The effect of transfer of chemically reactive species in the laminar flow over a stretching sheet is explained by Andersson et al. (1994). Afify (2004) explicated the MHD free convective flow of viscous incompressible fluid and mass transfer over a stretching sheet with chemical reaction. There are some fluids which react chemically with some ingredients present in them.
The boundary-layer flows of non-Newtonian fluids have been given considerable attention due to ever increasing engineering applications. In order to obtain a thorough cognition of non-Newtonian fluids and their various applications, it is necessary to study their flow behaviors. It is well known that the mechanics of non-Newtonian fluids present a special challenge to engineers, physicists and mathematicians. The non-linearity can manifest itself in a variety of ways in many fields, such as food processing, drilling operations and bio-engineering. Furthermore, in order to obtain a thorough cognition of non-Newtonian fluids and their various applications, it is necessary to study their flow behaviors. Due to their application in industry and technology, few problems in fluid mechanics have enjoyed the attention that has been accorded to the flow which involves non-Newtonian fluids. It is well known that mechanics of non-Newtonian fluids present a special challenge to engineers, physicists and mathematicians. The non-linearity can manifest itself in a variety of ways in many fields, such as food, drilling operations and bio-engineering. The Navier-Stokes theory is inadequate for such fluids, and no single constitutive equation is available in the literature which exhibits the properties of all fluids. Because of the complexity of these fluids, there is not a single constitutive equation which exhibits all properties of such non-Newtonian fluids. Thus, a number of non- Newtonian fluid models have been proposed. In the literature, the vast majority of non-Newtonian fluid models are concerned with simple models like the power law and grade two or three (Andersson and Dandapat, 1992; Hassanien, 1996; Sajid et al., 2009; Siddiqui et al., 2008; Serdar and Salih Dokuz, 2006).
These simple fluid models have shortcomings that render to results not having accordance with fluid flows in the reality. Casson fluid is another fluid model for non-Newtonian fluid. In the literature, the Casson fluid model is sometimes stated to fit rheological data better than general viscoplastic models for many materials (Mustafa et al., 2011; Bhattacharyya et al., 2013). Examples of Casson fluid include jelly, tomato sauce, honey, soup and concentrated fruit juices, etc. Human blood can also be treated as Casson fluid. Due to the presence of several substances like, protein, fibrinogen and globulin in aqueous base plasma, human red blood cells can form a chainlike structure, known as aggregates or rouleaux. If the rouleaux behave like a plastic solid, then there exists a yield stress that can be identified with the constant yield stress in Casson's fluid (Fung, 1984; Kandasamy and Pai, 2012; Nadeem et al., 2102; 2013a;b). The nonlinear Casson's constitutive equation has been found to describe accurately the flow curves of suspensions of pigments in lithographic varnishes used for preparation of printing inks (Casson, 1959) and silicon suspensions (Walawender et al., 1975). The shear stress-shear rate relation given by Casson satisfactorily describes the properties of many polymers Vinogradov and Malkin (1979) over a wide range of shear rates. Casson fluid can be defined as a shear thinning liquid which is assumed to have an infinite viscosity at zero rate of shear, a yield stress below which no flow occurs, and a zero viscosity at an infinite rate of shear (Dash et al., 1996). Eldabe and Salwa (1995) have studied the Casson fluid for the flow between two rotating cylinders, and Boyd et al. (2007) investigated the Casson fluid flow for the steady and oscillatory blood flow.
In this contribution a special form of Lie group transformations, known as scaling group of transformation is used in this paper to find out the full set of symmetries of the problem of the boundary layer flow due to stretching plane with mass transfer is studied. Motivated by the abovementioned investigations and applications, we venture further in the regime of two-dimensional boundary layer flows of a non-Newtonian fluid over an inclined surface with uniform magnetic field and first order of chemical reaction effect using Lie group analysis. Casson fluid model is used to characterize the non-Newtonian fluid behavior.
II. MATHEMATICAL FORMULATION
Consider steady state, natural convection of heat and mass transfer in laminar boundary layer flow of a non-Newtonian Casson fluid with uniform magnetic field normal to the plate and first order chemical reaction along a semi-infinite inclined plate with an acute angle from the vertical. The surface is maintained at a constant temperature Tw which is higher than the constant temperature T∞ of the surrounding fluid and the surface concentration Cw is greater than the surrounding fluid concentration C∞. The fluid properties are assumed to be constant except density in the buoyancy term. It is assumed that the effect of viscous dissipation is negligible in energy equation and there is a first-order chemical reaction between the diffusing species and the fluid. The Casson fluid model is used to characterize the non-Newtonian fluid behavior. The x-axis is taken along the plate and the y-axis is taken perpendicular to the plate. The fluid experiences a second-order slip at the sheet surface. On the other hand, the rheological equation of state for an isotropic and incompressible flow of a Casson fluid as (Mustafa et al., 2011)
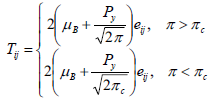
where, Tij is the (i,j)-th component of the stress tensor, tij =eij eij and eij are the (i,j)-th component of the deformation rate, π is the product of the component of deformation rate with itself, πc is a critical value of this product based on the non-Newtonian model, μB is plastic dynamic viscosity of the non-Newtonian fluid, and Py is the yield stress of the fluid. So, if a shear stress less than the yield stress is applied to the fluid, it behaves like a solid, whereas if a shear stress greater than yield stress is applied, it starts to move. Considering the balance laws of mass, linear momentum and energy and with the help of Boussinesq's approximation the equations governing this flow can be written in the usual form as
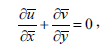 | (1) |
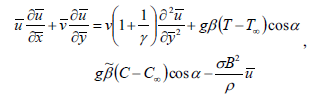 | (2) |
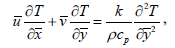 | (3) |
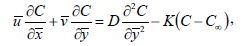 | (4) |
where 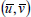 are the velocity components in
are the velocity components in 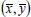 directions, respectively, n is the kinematic viscosity, C and T represent the concentration and temperature of the fluid, whereas C∞ and T∞ are the ambient concentration and temperature,
directions, respectively, n is the kinematic viscosity, C and T represent the concentration and temperature of the fluid, whereas C∞ and T∞ are the ambient concentration and temperature,  and B are the fluid electrical conductivity and magnetic field of uniform strength, γ is the Casson parameter. β and
and B are the fluid electrical conductivity and magnetic field of uniform strength, γ is the Casson parameter. β and 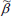 are the thermal and mass expansion coefficients and K is the chemical reaction parameter of the solute, D is the mass diffusivity, cp and ρ are the specific heat of the fluid and the density of the fluid. k is the thermal conductivity of fluid, α is the angle of inclination and γis the acceleration due to gravity. Considering the following boundary conditions for the governing equations
are the thermal and mass expansion coefficients and K is the chemical reaction parameter of the solute, D is the mass diffusivity, cp and ρ are the specific heat of the fluid and the density of the fluid. k is the thermal conductivity of fluid, α is the angle of inclination and γis the acceleration due to gravity. Considering the following boundary conditions for the governing equations
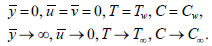 | (5) |
In order to get a non-dimensional form of governing equations we define the following transformations
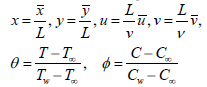 | (6) |
Substituting Eq. (6) into Eqs. (1) to (4) we get the following dimensionless governing equations
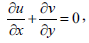 | (7) |
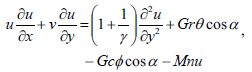 | (8) |
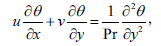 | (9) |
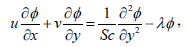 | (10) |
and the boundary conditions turn into
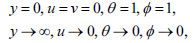 | (11) |
where Gr=gβ(Tw-T∞)L3v2 is the thermal Grashof number, Gc=gβ(Cw-C∞)L3v2 is the solutal Grashof number, Pr=ρcpvk-1 is the Prandtl number, Sc=vD-1is the Schmidt number, λ=KL2v1 is the non-dimensional chemical reaction parameter and Mn=σB2L2(ρv)-1 is the magnetic parameter.
III. LIE-POINT SYMMETRIES EQUATIONS
Asymmetry of a differential equation is an inevitable transformation of the dependent and independent variables that maps the equation to itself. Amongst symmetries of differential equations, those depending continuously on a small parameter and forming a local one-parameter group of transformation can be calculated algorithmically thanks to a procedure due to Sophus Lie (1842-1899). One of the most useful and striking properties of symmetries is that they map solutions to solutions. For partial differentials, symmetries allow the reduction of the number of independent variables. The one-parameter Lie group of infinitesimal transformations in 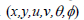 leaving (7)-(10) invariant is defined as
leaving (7)-(10) invariant is defined as
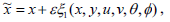 | (12a) |
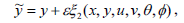 | (12b) |
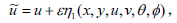 | (12c) |
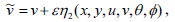 | (12d) |
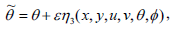 | (12e) |
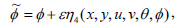 | (12f) |
where ε is the Lie group parameter. Requiring that Eqs. (7)-(10) are invariants under these transformations yields an over-determined, linear system of equations for infinitesimals 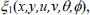
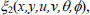
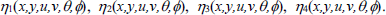
By carrying out a straightforward and tedious algebra, we finally obtain the form of the infinitesimals as
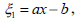 | (13a) |
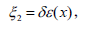 | (13b) |
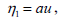 | (13c) |
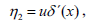 | (13d) |
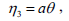 | (13e) |
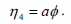 | (13f) |
Imposing the restrictions from boundaries and from the boundary conditions on the infinitesimals, we obtain the following form for Eq. (13)
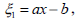 | (14a) |
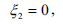 | (14b) |
 | (14c) |
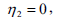 | (14d) |
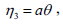 | (14e) |
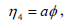 | (14f) |
where the parameter a represents the scaling transformation and parameter b represents translation in the x coordinate.
IV. REDUCTION TO ORDINARY DE.
We will produce the similarity transformation and solutions using the infinitesimals given in Eqs. (14). Leaving the details of the procedure to Bluman and Kumei (1989), we choose only the scaling transformation (i.e. a=1, b=0).
The characteristic equations are
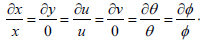 | (15) |
From which the similarity variable, the velocities, the temperature and concentration turn to be of the form
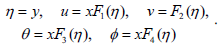 | (16) |
Finally, substituting (16) into Eqs. (7)-(10), we obtain the system of nonlinear ordinary differential equations
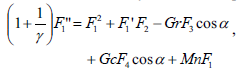 | (17) |
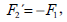 | (18) |
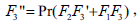 | (19) |
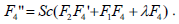 | (20) |
The appropriate boundary conditions are expressed as
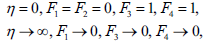 | (21) |
Nusselt and Sherwood numbers are defined respectively as
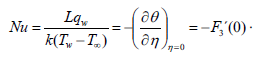 | (22) |
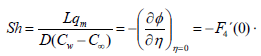 | (23) |
In addition, the shearing stress on the surface is
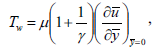 | (24) |
Since the local skin-friction coefficient Cf is defined by
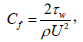 | (25) |
where U is a characteristic velocity. Substituting Eq. (24) into Eq. (25) in terms of the non-dimensional quantities, we obtain
 | (26) |
here Re=LU/v is the Reynolds number.
V. RESULTS AND DISCUSSION
The system of ordinary differential Eqs. (17)-(20) subject to the boundary conditions (21) was solved numerically using the fourth order Runge-Kutta scheme with shooting techniques with a systematic guessing of F1'(0), F3' and F4'(0), the guess should satisfy the boundary conditions and reveal the behavior of the solution. To overcome this difficulty, we start with a set of parameter values for which the problem is easy to be solved. Then, we use the obtained result as initial guess
for the solution of the problem with small variation of the parameters. This is repeated until the right values of the parameters are reached. The procedure is repeated until we get the results up to the desired degree of accuracy, namely 10□-5 . All calculations are obtained for Casson fluid when γ=2.6, λ=0.7, Sc=1.3, Mn=0.1, Gr=0.5, α=0°, Pr=7.0 and Newtonian fluid (γ→∞).
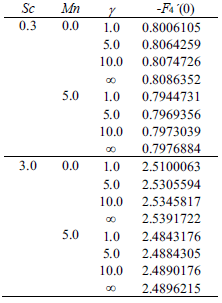
Table 1 and 2 represent the values of heat and mass transfer in terms of Nusselt and Sherwood number for various values of Prandtl number, Schmidt number, Magnetic field parameter and Casson parameter. It is observed that as both of Prandtl number and Casson parameter increase the Nusselt number increases and as Schmidt number and Casson parameter increase the Sherwood number increases while the magnetic field parameter tends to decrease both of Nusselt and Sherwood numbers.
Table 1. Values of Nusselt number for different values of Pr, Mn and γ
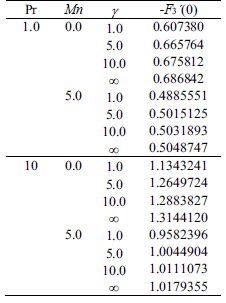
Table 2. Values of Sherwood number for different values of Sc, Mn and γ
Figures 1(a)-(d) illustrate the influence of Casson parameter γ on x and y velocities, temperature and concentration distributions respectively, considering the two cases of Casson and Newtonian fluids. The increasing values of the Casson parameter i.e. the decreasing yield stress (the fluid behaves as Newtonian fluid as Casson parameter becomes large) suppress the velocity field. The effect of increasing values of γ is to reduce the rate of transport, and hence, the boundary layer thickness decreases. It is observed that F1 and F2 and the associated boundary layer thickness are decreasing function of γ. The effect of increasing γ leads to decrease the temperature and concentration field for steady motion Figs. 1 (c) and (d). It can also be seen from Fig. 1 that the momentum boundary layer thickness decreases as γincreases and hence induces an increase in the absolute value of the velocity gradient at the surface. On the other hand, first the peak of the velocity at the surface increasing with γ until critical value of η (2.14) then the velocity decreases. The effect of the chemical reaction parameter γ=0.3, 0.6, 1.0, 1.6, 2.0 and 5.0 on the x component velocity and concentration distributions is displayed in Figs. 2(a) and (b). The velocity increases with increasing the chemical reaction parameter until certain value of η»2.12 and after this value an opposite behavior occur, see Fig. 2(a), whereas the effects of the chemical reaction parameter and the Schmidt number are very important in the concentration field. It is observed from Figs. 2(b) and 3 that concentration profiles decrease with increasing the chemical reaction parameter and Schmidt number and the thickness of the concentration boundary layer decreases with increasing the Schmidt number.
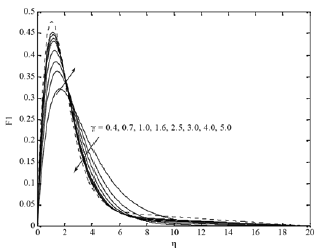
Fig. 1(a). F1 profiles for various values of γ.
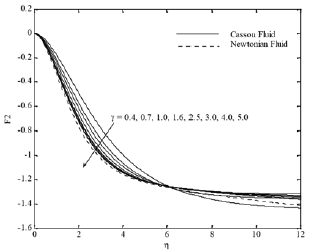
Fig. 1(b). F2 profiles for various values of γ.
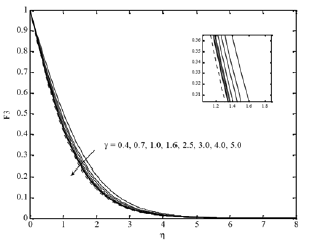
Fig. 1(c). F3 profiles for various values of γ.
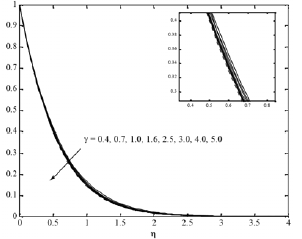
Fig. 1(d). F4 profiles for various values of γ.

Fig. 2(a). F1 profiles for various values of l.
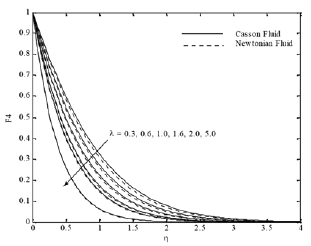
Fig. 2(b). F4 profiles for various values of l.
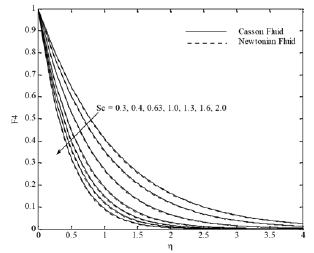
Fig. 3. F3 profiles for various values of Sc.
The effect of Prandtl number on temperature profiles is as the effect of Schmidt number on concentration profiles, i.e. an increase in the Prandtl number tends to decrease the temperature distributions (Fig. 4). This is in agreement with the physical fact that the thermal boundary layer thickness decreases with increase in the Prandtl number. The reason for such a behavior is that the high Prandtl number fluid has a relatively low thermal conductivity. This results in the reduction of the thermal boundary layer thickness.
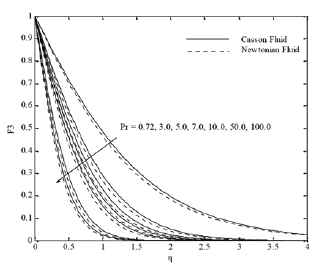
Fig. 4. F3 profiles for various values of Pr.
Figures 5(a)-(d) depict the influences of Grashof number on the velocity, temperature and concentration distributions. It is seen from Fig. 5(a) that the x component of the velocity increases with the thermal Grashof number because the favorable buoyancy force accelerates the fluid, but the y component of the velocity decreases. In addition, the temperature and concentration decrease with increasing the thermal Grashof number. Consequently the thermal and solutal boundary layer thicknesses are reduced.
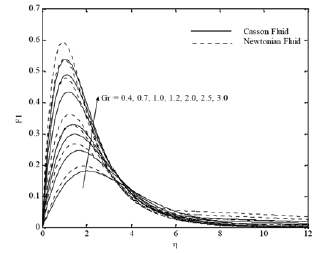
Fig. 5(a). F1 profiles for various values of Gr.
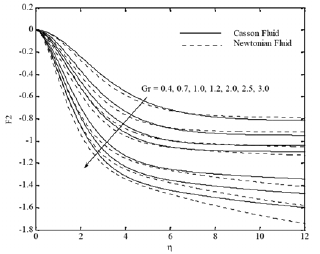
Fig. 5(b). F2 profiles for various values of Gr.
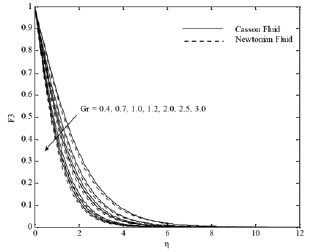
Fig. 5(c). F3 profiles for various values of Gr.
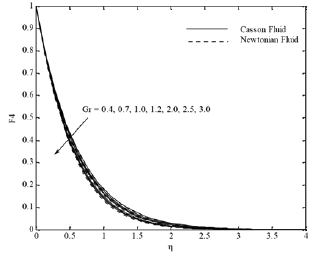
Fig. 5(d). F4 profiles for various values of Gr.
Furthermore, an opposite behavior occurs with solutal Grashof number Fig. 6 (a)-(d). The effect of the inclination of the surface for different parameters is displayed in Figs. 7(a)-(d). It is found that x velocity component decreases with increasing the inclination angle, whereas the y velocity component, temperature and concentration profiles increase. This is because of the fact that the buoyancy flow decreases due to gravity
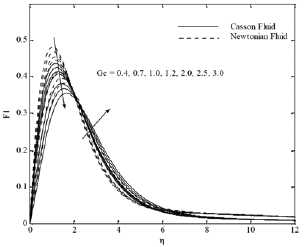
Fig. 6(a). F1 profiles for various values of Gc
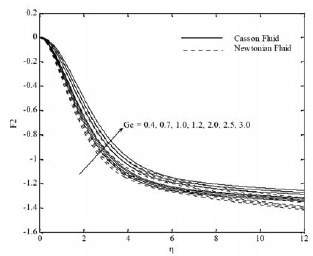
Fig. 6(b). F2 profiles for various values of Gc
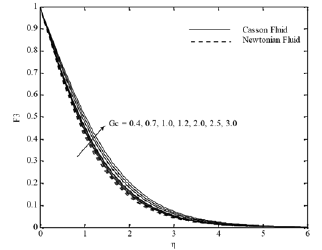
Fig. 6(c). F3 profiles for various values of Gc
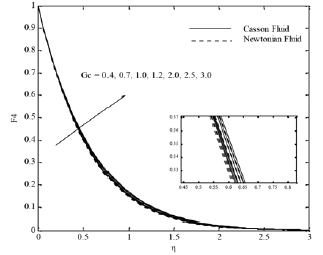
Fig. 6(d). F4 profiles for various values of Gc
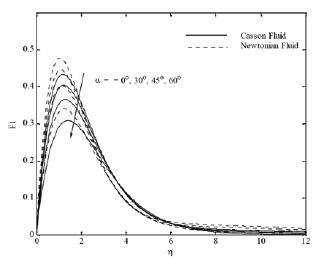
Fig. 7(a). F1 profiles for various values of a
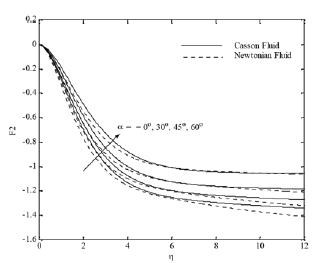
Fig. 7(b). F2 profiles for various values of a
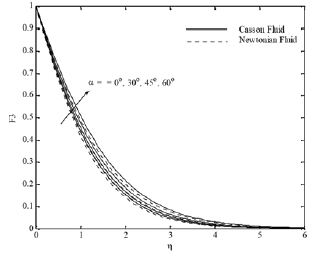
Fig. 7(c). F3 profiles for various values of a
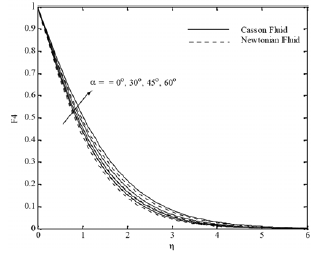
Fig. 7(d). F4 profiles for various values of a
components. γ cos α as the surface is inclined. The effect of magnetic field parameter is shown in Figs. 8(a)-(d). As it is clear that the magnetic field parameter makes the x velocity component, temperature and concentration increase.
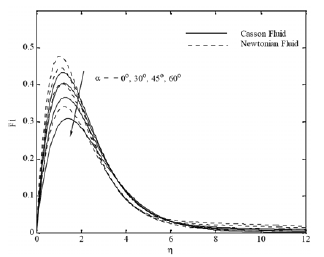
Fig. 8(a). F1 profiles for various values of Mn
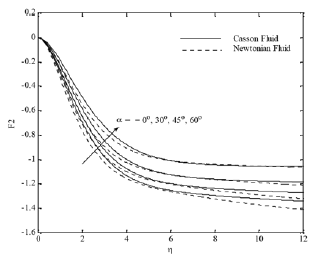
Fig. 8(b). F2 profiles for various values of Mn
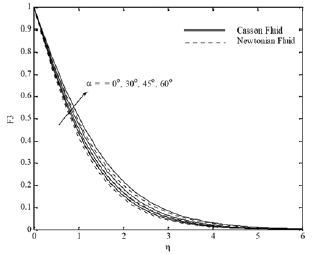
Fig. 8(c). F3 profiles for various values of Mn

Fig. 8(d). F4 profiles for various values of Mn
VI. CONCLUSIONS
The symmetries of the governing system of partial differential equations are obtained using Lie group analysis and they reduce the system to system of ordinary differential equations via scaling transformation. Numerical solutions of the ordinary differential equations are also obtained.
From the numerical results, it is observed that the effect of increasing values of the Casson parameter γ is to suppress the velocity field, temperature and the species concentration. The thickness of the momentum boundary layer increases with increasing the chemical reaction
parameter and the Schmidt number. The thicknesses of the thermal and concentration boundary layers are decreased with increasing the chemical reaction parameter, thermal Grashof number and the Schmidt number. It is also found that the velocity increases with increasing the Grashof number. The thickness of the thermal boundary layer decreases with increasing the Prandtl number, where as the concentration boundary layer thickness increases with the Prandtl number
REFERENCES
1. Afify, A., "MHD free convective flow and mass transfer over a stretching sheet with chemical reaction," Heat Mass Transfer, 40, 495-500 (2004).
2. Andersson, H.I. and B.S. Dandapat, "Flow of a power-law fluid over a stretching sheet," Appl. Anal. Continuous Media, 1 339-347 (1992).
3. Anderson, H.I., O.R. Hansen and B.Holmedal, "Diffusion of a chemically reactive species from a stretching sheet," Int. J. Heat mass Transfer, 37, 659-664 (1994).
4. Bhattacharyya, K., T. Hayat and A. Alsaedi, "Analytic solution for magnetohydrodynamic boundary layer flow of Casson fluid over a stretching/shrinking sheet with wall mass transfer," Chin. Phys. B, 22 024702 (2013).
5. Bhuvaneswari, M., S. Sivasankaran and M. Ferdows, "Lie group analysis of natural convection heat and mass transfer in an inclined surface with chemical reaction," Nonlinear Analysis: Hybrid Systems, 3, 536-542 (2009).
6. Bluman, G.W. and S. Kumei, Symmetries and differential equations, Applied Mathematical Sciences, Springer, Berlin, New York (1989).
7. Boyd, J., J.M. Buick and S. Green, "Analysis of the Casson and Carreau-Yasuda non-Newtonian blood models in steady and oscillatory flow using the lattice Boltzmann method," Phys. Fluids, 19, 93-103 (2007).
8. Casson, N. In: Mill CC, editor. Rheology of dispersed system, 84, Pergamon Press, Oxford (1959).
9. Chambre, P.L. and J.D. Young, "On diffusion of a chemically reactive species in a laminar boundary layer flow," Phys. Fluids, 1, 48-54 (1958).
10. Dash, R.K., K.N. Mehta and G. Jayaraman, "Casson fluid flow in a pipe filed with a homogeneous porous medium," Int. J Eng. Sci., 34, 1145-1156 (1996).
11. Eldabe, N.T.M. and M.G.E. Salwa, "Heat transfer of MHD non-Newtonian Casson fluid flow between two rotating cylinder," J. Phys. Soc. Jpn., 64, 41-64 (1995).
12. Ferdows, M., M.J. Uddin and A. Afify, "Scaling group transformation for MHD boundary layer free convective heat and mass transfer flow past a convectively heated nonlinear radiating stretching sheet," Int. J. Heat Mass Transfer, 56, 181-187 (2013a).
13. Ferdows, M., M.J. Uddin, M.M. Rashidi and N. Rahimzadeh, "Numerical analysis of mixed convection over horizontal moving porous flat plate by the method of one parameter continuous group theory," Int. J. Numer. Methods Heat Fluid Flow, 23, 729-749 (2013b).
14. Fung, Y.C., Biodynamics circulation, Springer Verlag; New York (1984).
15. Hamad, M., M.J. Uddin and A. Ismail, "Investigation of combined heat and mass transfer by lie group analysis with variable diffusivity taking into account hydrodynamic slip and thermal convective boundary conditions," Int. J. Heat Mass Transfer, 55, 1355-1362 (2012).
16. Hassanien, I.A., "Flow and heat transfer on a continuous flat surface moving in a parallel free stream of power-law fluid," Appl. Model, 20, 779-784 (1996).
17. Ibragimov, N.K., CRC Handbook of Lie Group Analysis of Differential Equations, Symmetries, Exact Solutions, and Conservation Laws, 1, CRC Press Llc (1994).
18. Jalil, M. and S. Asghar, "Flow of power-law fluid over astretching surface: a lie group analysis," Int. J. Non-Linear Mech., 48, 65-71 (2013).
19. Jalil, M., S. Asghar, and M. Mushtaq, "Lie group analysis of mixed convection flow with mass transfer over a stretching surface with suction or injection," Math. Prob. Eng., 264901 (2010).
20. Jalil, M., S. Asghar and S.M. Imran, "Self similar solutions for the flow and heat transfer of Powell-Eyring fluid over a moving surface in a parallel free stream," Int. J. Heat Mass Transfer, 65, 73-79 (2013).
21. Kandasamy, A. and R.G. Pai, "Entrance region flow of Casson fluid in a circular tube," Appl. Mech. Mater 110/116, 698-706 (2012).
22. Mustafa, M., T. Hayat, I. Pop,and A. Aziz, "Unsteady boundary layer flow of a Casson fluid due to an impulsively started moving flat plate," Heat Transfer - Asian Res., 40, 563-576 (2011).
22. Nadeem, S., R.U. Haq and C.Lee, "MHD flow of a Casson fluid over an exponentially shrinking sheet," Sci. Iran, 19, 1550-1553 (2012).
23. Nadeem, S., R.U. Haq and N. S. Akbar, "MHD threedimensional boundary layer flow of Casson nanofluid past a linearly stretching sheet with convective boundary condition, IEEE Transactions Nanotechnology, 13, 109-115 (2013a).
24. Nadeem, S., R.U. Haq, N.S. Akbar and Z.H. Khan, "MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet," Alexandria Engineering Journal, 52, 577-582 (2013b).
25. Olver, P., Application of Lie groups to differential equations, Graduate Texts in Mathematics, 107, Springer, New York (1986).
26. Sajid, M., I. Ahmad, T. Hayat and M. Ayub, "Unsteady flow and heat transfer of a second grade fluid over a stretching sheet," Commun. Nonlinear Sci. Numer. Simul., 14, 96-108 (2009).
27. Serdar, B. and M. Salih Dokuz, "Three-dimensional stagnation point flow of a second grade fluid towards a moving plate," Int. J. Eng. Sci., 44, 49-58 (2006).
28. Siddiqui, A.M., A. Zeb, Q.K.. Ghori and A.M. Benharbit, "Homotopy perturbation method for heat transfer flow of a third grade fluid between parallel plates," Chaos Solitons Fractals, 36 182-192 (2008).
29. Vinogradov, G.V. and A.Y. Malkin, Rheology of polymers, Mir Publisher, Moscow (1979).
30. Walawender W.P., T.Y. Chen and D.F. Cala, "An approximate Casson fluid model for tube flow of blood," Biorheology, 12, 111-119 (1975).
Received: February 17, 2014.
Accepted: October 8, 2014.
Recommended by Subject Editor: Walter Ambrosini.