Servicios Personalizados
Articulo
Latin American applied research
versión On-line ISSN 1851-8796
Lat. Am. appl. res. vol.45 no.2 Bahía Blanca abr. 2015
Rotation of a porous approximate sphere in an approximate spherical container
D. Srinivasacharya and M. Krishna Prasad
Department of Mathematics, National Institute of Technology, Warangal-506 004, A.P., India. Tel.: +91 870 2462821 Fax: +91 870 2459547 Email: dsc@nitw.ac.in, dsrinivasacharya@yahoo.com, kpm973@gmail.com
Abstract— The problem of steady rotation of a porous approximate sphere located at the center of an approximate spherical container has been investigated. The Brinkman's model for the flow inside the porous approximate sphere and the Stokes equation for the flow in an approximate spherical container were used to study the motion. The torque experienced by the porous approximate spherical particle in the presence of cavity is obtained and wall correction factor is calculated. The special cases of rotation of a porous sphere and a solid sphere in a spherical container are obtained from the present analysis.
Keywords— Rotation; Porous Approximate Sphere; Stokes Flow; Brinkman Equation; Stress Jump Coefficient.
I. INTRODUCTION
Fluid flows past rotating axially symmetric bodies are of fundamental and received considerable attention due to their practical interest in the areas of chemical, biomedical and environmental engineering and science. One of the important physical quantities, which is needed in different applications, is the couple experienced by steadily rotating bodies in an incompressible viscous fluid. The couple experienced by a rotating body is required for designing and calibration of viscometers (Kanwal, 1961). A survey of literature regarding the fluid flows past and within porous bodies indicates that while abundant information is available for flows in an infinite expanse of fluid, very little information is available for flows in enclosures. Cunningham (1910) and Williams (1915), independently, considered the motion of a solid sphere in a spherical container. They presented solutions for the case of an inner solid sphere. Haberman and Sayre (1962) have made an analogous study for the motion of an inner Newtonian fluid sphere. All the above authors used no-slip condition on the surface of the inner sphere. Ramkissoon and Rahaman (2001, 2003) investigated the motion of inner non-Newtonian (Reiner-Revlin) fluid sphere in a spherical container and a solid spherical particle in a spheroidal container. They evaluated the expression for drag on the inner sphere and examined the wall effects.
The flow problems of the motion of a porous particle in a container have been modeled by using the Stokes version of the Navier-Stokes equation for the flow inside the container and Darcy's law or Brinkman's equation to describe the flow within the porous particle. The boundary condition for the flow field across a porous-liquid interface has drawn the attention of many researchers. Several types of boundary conditions at the interface of the free fluid and porous region to link the different flow regimes were suggested in literature. One type amongst them is continuity of the velocity, pressure and tangential stresses at the porous-liquid interface. Using this condition, the quasi-steady translation and steady rotation of a spherically symmetric composite particle composed of a solid core and a surrounding porous shell located at the center of a spherical cavity filled with an incompressible Newtonian fluid is studied by Keh and Chou (2004). The quasi-steady translation and steady rotation of a spherically symmetric porous shell located at the center of a spherical cavity filled with an incompressible Newtonian fluid is investigated analytically by Keh and Lu (2005). They evaluated the hydrodynamic drag force and torque exerted by the fluid on the porous particle and found that the boundary effects of the cavity wall on the creeping motions of a composite sphere can be significant in appropriate situations. Srinivasacharya (2005) studied the motion of a porous sphere in a spherical container. The flow problem of an incompressible axisymmetrical quasi-steady translation and steady rotation of a porous spheroid in a concentric spheroidal container are studied analytically by Saad (2010). Motivated by an interest in the interaction of cells or microspheres with the glycocalix, Damiano et al. (2004) have obtained exact solutions to the problem of translational and rotational motion of a sphere in a Stokes flow near a Brinkman medium.
Ochoa-Tapia and Whitaker (1995 a, b) have investigated the boundary conditions at the porous-liquid interface by applying volume average techniques. They have shown that the equations require a discontinuity in the shearing stress but continuity in velocity components and normal stress. Ochoa-Tapia has derived the stress jump boundary condition
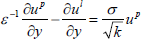 |
where up, ul are tangential velocity components in porous region and liquid region respectively, ε is the porosity, k is the permeability of the homogeneous portion of the porous region and σ is the stress jump coefficient. If σ ≠ 0, there is a discontinuity in the shear stress at the porous-liquid interface. This jump condition is constructed to join Darcy's law with the Brinkman correction to Stokes equations. Experimentally it has been verified that the jump coefficient σ varies in the range −1 to 1 (Ochoa-Tapia and Whitaker, 1995a,b), Kuznetsov 1996, 1998). Kuznetsov (1996, 1998) used this stress jump boundary condition at the interface between a porous medium and a clear fluid to discuss flow in channels partially filled with porous medium. Raja Sekhar and Bhattacharyya (2005) have used stress jump boundary condition while discussing the Stokes flow of a viscous fluid inside a sphere with internal singularities, enclosed by a porous spherical shell. They concluded that the fluid velocity at a porous-liquid interface varies with the stress jump coefficient and it plays an important role in describing the flow field associated with porous medium. The flow of a viscous fluid in a spherical annulus formed by a solid sphere rotating with a constant angular velocity and a concentric spherical porous medium has been discussed by Srivastava and Saxena (2008) using this stress jump boundary condition. They concluded that the torque on the rotating sphere also increases with the decrease of the permeability of the porous medium.
In this paper, we consider slow steady rotation of a porous approximate sphere in an approximate spherical container. We have used the Brinkman's model for the flow inside the porous approximate sphere and Stokes' model for the flow within the approximate spherical container. The flow examined is axially symmetric in nature. As boundary conditions, continuity of the velocity and the slip condition at the porous-liquid interface proposed by Ochoa-Tapia and Whitaker are employed. The hydrodynamic torque acting on the porous approximate sphere in the presence of the cavity and wall effects are studied numerically.
II. FORMULATION OF THE PROBLEM
Let (r, θ, f) denote a spherical polar co-ordinate system with origin at the center of a sphere r=a with 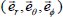 are unit base vectors. Consider the body
are unit base vectors. Consider the body 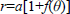 , where f(θ) is a function of θ which can be expressed as
, where f(θ) is a function of θ which can be expressed as 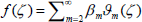 , where
, where 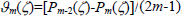 , ζ=cos(q) in which Pm(ζ) is the Legendre function of the first kind. ϑm(ζ) is the Gegenbauer function of the first kind of order m and degree −1/2 (Happel and Brenner, 1965). For small βm 's we refer to this body as an approximate sphere. If all βm are zero, the approximate sphere reduces to a sphere of radius a.
, ζ=cos(q) in which Pm(ζ) is the Legendre function of the first kind. ϑm(ζ) is the Gegenbauer function of the first kind of order m and degree −1/2 (Happel and Brenner, 1965). For small βm 's we refer to this body as an approximate sphere. If all βm are zero, the approximate sphere reduces to a sphere of radius a.
Consider the slow steady rotation of a porous approximate spherical particle located at the center of an approximate spherical vessel containing an incompressible Newtonian viscous fluid (see Fig.1). Assume that the approximate spherical particle is rotating slowly with angular speed Ω about the axis of symmetry θ=0. Let the equation of the porous approximate spherical particle be 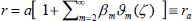 and that of approximate spherical vessel be
and that of approximate spherical vessel be 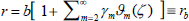 .
.
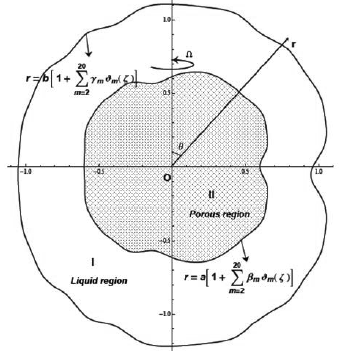
Figure 1: The physical situation and the coordinate system (m=20, b=1, a=0.6).
Assume that the flow within the approximate spherical container (i.e. ra≤r≤rb) is governed by the Stokes' approximation to Navier-Stokes equations,
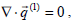 | (1) |
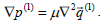 | (2) |
and the flow inside the porous approximate sphere (i.e., r≤ra) is governed by Brinkman's equations,
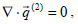 | (3) |
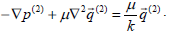 | (4) |
where 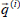 is the volumetric average of the velocity, μ is the coefficient of viscosity, p(i) is the average of the pressure and k is the permeability of the porous medium.
is the volumetric average of the velocity, μ is the coefficient of viscosity, p(i) is the average of the pressure and k is the permeability of the porous medium.
Since flow is axially symmetric about the axis of rotation, all the physical quantities are independent of  . Hence, we assume that the velocity vectors
. Hence, we assume that the velocity vectors 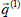 and
and 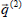 in the form
in the form
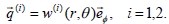 | (5) |
Substituting (5) in (2) and (4) and after simplification, we get the following dimensionless equations
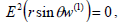 | (6) |
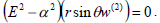 | (7) |
where α2=a2/k and E2= ∂2/∂r2+ (1−ζ2)/r2 ∂2/∂r2 is the Stokesian stream function operator.
III. BOUNDARY CONDITIONS
The boundary conditions are
(i) Continuity of velocity component on the boundary of the porous approximate sphere, i.e.,
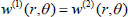 on r = ra, on r = ra, | (8) |
(ii) Ochoa-Tapia's stress jump boundary condition for tangential stress, i.e.,
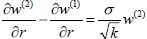 on r = ra, on r = ra, | (9) |
where σ is the stress jump coefficient.
(iii) on the cell surface
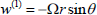 on r = rb, on r = rb, | (10) |
The boundary conditions from Eqs. (8) to (10) in dimensionless form are
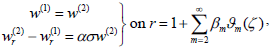 | (11) |
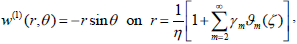 | (12) |
where η = a/b.
IV. SOLUTION OF THE PROBLEM
The solution of (6) is
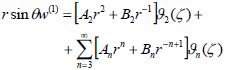 | (13) |
and the solution of (7) is
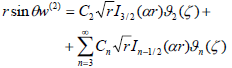 | (14) |
where In−1/2(αr) denote the modified Bessel function of the first kind of order n − 1/2.
V. DETERMINATION OF ARBITRARY CONSTANTS
We first develop the solution corresponding to the boundaries 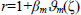 and
and 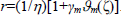 . Assuming that the coefficients βm and γm are sufficiently small that squares and higher powers may be neglected (Happel and Brenner, 1965). Comparison of the above solution with those obtained in case of motion of porous sphere in a spherical container (Srinivasacharya, 2005), indicates that the terms involving An, Bn and Cn for n>2 are the extra terms here which are not present in the case of sphere. The body that we are considering now is an approximate sphere and the flow generated is not expected to be far different from the one generated by rotation of a porous sphere. Also the coefficients An, Bn and Cn for n>2 are of order βm and the coefficients An, Bn for n> 2 are of order γm. Therefore, while implementing the boundary conditions, we ignore the departure from the spherical form and set in (11) r= 1 in the terms involving An, Bn and Cn for n>2 and in (12) r=1/η in the terms involving An and Bn for n> 2.
. Assuming that the coefficients βm and γm are sufficiently small that squares and higher powers may be neglected (Happel and Brenner, 1965). Comparison of the above solution with those obtained in case of motion of porous sphere in a spherical container (Srinivasacharya, 2005), indicates that the terms involving An, Bn and Cn for n>2 are the extra terms here which are not present in the case of sphere. The body that we are considering now is an approximate sphere and the flow generated is not expected to be far different from the one generated by rotation of a porous sphere. Also the coefficients An, Bn and Cn for n>2 are of order βm and the coefficients An, Bn for n> 2 are of order γm. Therefore, while implementing the boundary conditions, we ignore the departure from the spherical form and set in (11) r= 1 in the terms involving An, Bn and Cn for n>2 and in (12) r=1/η in the terms involving An and Bn for n> 2.
Using the observations made above and the boundary conditions (11) and (12) in the expressions (13) and (14) and equating leading coefficients to zero in the resulting equations, we get a system of equations in A2, B2 and C2. Solving this system of equations, we get
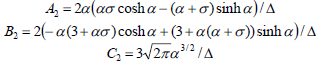 | (15) |
where
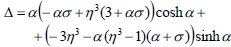 | (16) |
Using the identities given in Happel and Brenner (1965), (p.142), we get An=Bn=Cn=0 for n≠m−2, m, m+2 and another system of equations in An, Bn and Cn for n=m−2, m, m+2. Solving this system of equations, we get the expressions for the arbitrary constants An, Bn and Cn for n=m−2, m, m+2. As the expressions for these constants are lengthy, they have not presented here. Now, we employ the same technique to the boundaries
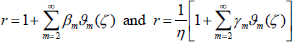 |
for each value of m. The final solution appears to be a superposition of the solutions for all m. Thus the velocity components of both flow regions are given by
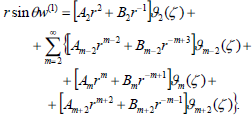 | (17) |
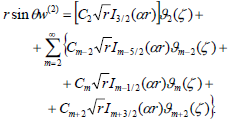 | (18) |
VI. TORQUE ON THE BODY AND WALL EFFECTS
The hydrodynamic couple acting on the porous approximate sphere in an approximate spherical container is obtained as
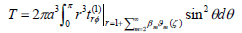 | (19) |
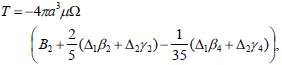 | (20) |
where
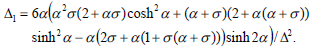 | (21) |
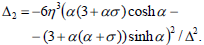 | (22) |
If b →∞ (or η=0), the couple exerted on the rotating porous approximate sphere in an unbounded medium is
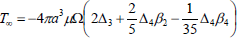 | (23) |
where
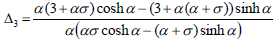 | (24) |
 | (25) |
The wall correction factor Wc is defined as the ratio of the actual couple experienced by the particle in the enclosure and the couple on a particle in an infinite expanse of fluid. With the aid of Eqs. (20) and (23) this becomes
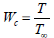 | (26) |
Note that Wc=1 for η = 0 and Wc ≥ 1 for 0 <η ≤ 1.
VII. SPECIAL CASES
A. Porous sphere in a spherical container
If βm=0 and γm=0 for m≥2, the inner and outer approximate spheres reduces to spheres. The hydrodynamic couple acting on the porous sphere in an spherical container is obtained as
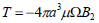 | (27) |
The wall correction factor Wc is
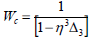 | (28) |
A.1. Porous sphere in a spherical container using continuity of stresses at the porous-liquid interface
For the steady rotational motion of a porous sphere in a spherical container with continuity of stress σ=0, the expression for the hydrodynamic torque becomes
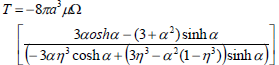 | (24) |
which agrees with the result obtained by Keh and Lu (2005), Saad (2010).
The wall correction factor Wc is given by
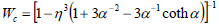 | (30) |
A.2. Solid sphere in a spherical container
In the limiting case of α→∞(or k = 0),
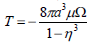 | (31) |
This is the result for the rotation of an impermeable solid sphere in a cell model (Saad, 2010).
The Wall correction factor Wc is given by
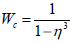 | (32) |
which is well-known result obtained in Keh and Lu (2005), Saad (2010).
VIII. RESULTS AND DISCUSSION
The variation of wall correction factor Wc with permeability k1(=1/α) is plotted in Fig. 2 for different values of σ and β2=β4=β (inner deformation parameter), γ2=γ4=γ (outer deformation parameter), separation parameter η are fixed . The validity of σ values (Ochoa-Tapia and Whitaker, 1995 a, b; Kuznetsov, 1996, 1998) is examined so that the wall correction factor gives a physical significance. It is observed that increasing permeability parameter k1 decreases the wall correction factor or torque. Further, the wall correction factor or torque is decreasing for increasing values of the stress jump coefficient. For positive values of stress jump coefficient σ, there is a change in the behavior of Wc at a particular value of permeability. Beyond the value of this permeability, Wc < 1 which is not physically possible. Therefore, the positive values of σ can not be considered beyond that particular permeability. If negative σ is considered in the stress jump condition (9), the shear stress shows an increase at the external (liquid) flow region than that of the internal (porous) flow region. Due to this, a significant torque force is generated on the porous surface for any permeability. But, for positive values of σ, although the shear stress of the external region becomes low, for a particular range of permeability a significant torque exerts on the surface. It seen that the wall correction factor or torque is more effective for negative values of stress jump coefficient.
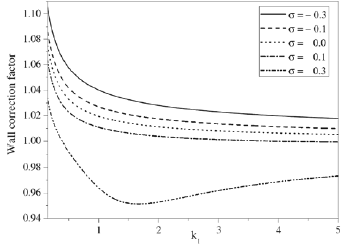
Figure 2: Variation of wall correction factor Wc with permeability k1 for different values of the stress jump coefficient σ; inner deformation parameter β=0.15, outer deformation parameter γ=0.1, separation parameter η=0.6.
The variation of wall correction factor Wc with permeability k1 for various values of β2=β4=β (inner deformation parameter) and γ2=γ4=γ (outer deformation parameter) are shown in Fig. 3 and Fig. 4 respectively, for fixed values of stress jump coefficient σ and separation parameter η. It can be noticed that there is an increase in the wall correction factor or torque as the deformation of the inner sphere β is increasing. It is interesting to note that the torque on the porous sphere is less than that of the torque on the porous approximate sphere in presence of cavity wall. It is observed from Fig. 4 that the correction factor Wc decreases as the stress jump coefficient increases.
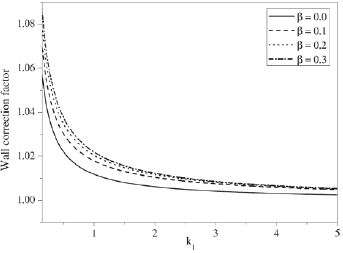
Figure 3: Variation of wall correction factor Wc with permeability k1 for different values of inner deformation parameter β; stress jump coefficient σ=0, outer deformation parameter γ=0.1, separation parameter η=0.6.
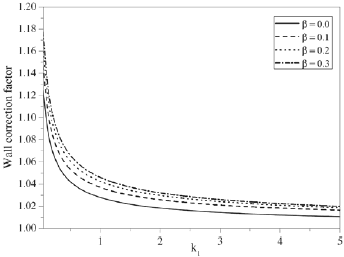
Figure 4: Variation of wall correction factor Wc with permeability k1 for different values of inner deformation parameter β; stress jump coefficient σ=−0.3, outer deformation parameter γ=0.1, separation parameter η=0.6.
The effect of the separation parameter η on wall correction factor Wc with permeability k1 is shown in Fig. 5. It is seen that the wall correction factor increases monotonically with an increase in the value of η. The boundary effect on the correction factor (or hydrodynamic torque) of the permeable particle is stronger when the permeability k1 is smaller. For k1<<1, the value of the correction factor of the porous sphere is close to that of a solid particle (with k1→0 and Wc is given by the Eq. 32) when η is small, while the difference is more significant as η→1. When the porous particle is in contact with the cavity wall (η=1), its correction factor does not vanish for cases with a finite value of α. Thus, the stress jump condition (9) can have a significant influence on the mobility of a particle. It is seen that Wc or torque not only depends on the separation parameter η and permeability k1 but also on the stress jump coefficient σ.
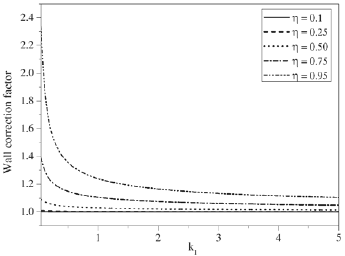
Figure 5: Variation of wall correction factor Wc with permeability k1 for different values of the separation parameter η; inner deformation parameter β=0.15, outer deformation parameter γ=0.1, stress jump coefficient σ=−0.5.
IX. CONCLUSIONS
An exact solution for the problem of steady rotation of a porous approximate sphere in an approximate spherical container is obtained by considering the Brinkman's law in the porous region and Stokes' equation in the liquid region. At the porous-liquid interface Ochoa -Tapia and Whitaker's stress jump condition, continuity of the velocity components have been used. An expression for the hydrodynamic torque acting on the porous sphere in the presence of the cavity and wall correction factor are obtained. The torque acting on the porous sphere is decreasing as the permeability k1 is increasing as well as the stress jump coefficient is increasing. Wall correction factor Wc increases as the separation parameter η increases.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge the referees for their constructive comments and valuable suggestions.
REFERENCES
1. Cunningham, E., "On the velocity of steady fall of spherical particles through fluid medium," Proc. Roy. Soc. London Ser., 83, 357-369 (1910).
2. Damiano, E.R., D.S. Long, F.H. El-Khatib and T.M. Stace, "On the motion of a sphere in a stokes flow parallel to a brinkman half-space," J. Fluid Mech., 500, 75-101 (2004).
3. Haberman, W.L. and R.M. Sayre, "Wall effects for rigid and fluid spheres in slow motion with a moving liquid," David Taylor model, Basin Report No.1143, Washington, DC (1958).
4. Happel, J and H. Brenner, Low Reynolds Number Hydrodynamics, Prentice-Hall, Englewood Cliffs, N.J. (1965).
5. Kanwal, R.P., "Slow steady rotation of axially symmetric bodies in a viscous fluid," J.Fluid Mech., 10, 17-24 (1961).
6. Keh, H.J. and J. Chou, "Creeping motion of a composite sphere in a concentric spherical cavity," Chem. Eng. Sci., 59, 407-415 (2004).
7. Keh, H.J and Y.S. Lu, "Creeping motions of a porous spherical shell in a concentric spherical cavity," J. Fluids and Structures., 20, 735-747 (2005).
8. Kuznetsov, A.V., "Analytical investigation of the fluid flow in the interface region between a porous media and a clear fluid in channels partially filled with porous medium," Appl. Sci. Research., 56, 53-67 (1996).
9. Kuznetsov, A.V., "Analytical investigation of couette flow in a composite channel partially filled with a porous media and partially with a clear fluid," Int. J. Heat Mass Transfer., 41, 2556-2560 (1998).
10. Ochoa-Tapia, J.A. and S. Whitaker, "Momentum transfer at the boundary between a porous medium and a homogeneous fluid-I, theoretical development," Int. J. Heat and Mass-Transfer., 38, 2635-2646 (1995a).
11. Ochoa-Tapia, J.A. and S. Whitaker, "Momentum transfer at the boundary between a porous medium and a homogeneous fluid-II, comparison with experiment," Int. J. Heat and Mass-Transfer., 38, 2647-2655 (1995b).
12. Raja Sekhar, G.P. and A. Bhattacharyya, "Stokes flow inside a porous spherical shell: Stress jump boundary condition," Z. Angew. Math. Phys., 56, 475-496 (2005).
13. Ramkissoon, H. and K. Rahaman, "Non Newtonian fluid sphere in a spherical container," Acta Mech., 149, 239-245 (2001).
14. Ramkissoon, H. and K. Rahaman, "Wall effects on a spherical particle," Int. J. Engrg. Sci., 41, 283-290 (2003).
15. Saad, E.I., "Translation and rotation of a porous spheroid in a spheroidal container," Can.J. Phys., 88, 689-700 (2010).
16. Srinivasacharya, D., "Motion of a porous sphere in a spherical container," C.R. Mecanique, 333, 612-616 (2005).
17. Srivastava, A.C and P. Saxena, "Rotation of a solid sphere in a viscous fluid bounded by a concentric spherical porous medium," J. Porous Media., 11, 575-588 (2008).
18. Williams, W.E., "On the motion of a sphere in a viscous fluid," Philos. Mag., 29, 526-550 (1915).
Received by Editorial Office: July 19, 2012.
Received by current Subject Editor: May 15, 2014.
Accepted: September 24, 2014.
Recommended by Subject Editor: Walter Tuckart.