Multi-objective reconfiguration of a distribution system including probabilistic loads and distributed generations

E. Ghandehari, E. Salleala-Naeeni and S. Shojaeian

Department of Electrical Engineering, Khomeinishahr Branch, Islamic Azad University, Isfahan, Iran Ebrahim.Ghandehari@iaukhsh.ac.ir, Ehsan.Salleala@iaukhsh.ac.ir, Shojaeian@iaukhsh.ac.ir

Abstract— The present study suggests a method to reconfigure a 13-bus distribution system which includes probabilistic loads (PLs) and Distributed Generations (DGs). Reconfiguration is a specific process to determine the best configuration of networks. It is usually assumed that loads are constant, while we know that they have probabilistic nature and change regularly, the above mentioned facts were taken into account in the current study. Considering that 3 DGs (wind farms) have been added to the distribution system, the generation is also probabilistic depending on weather change. The "Sifting Algorithm" has been used for reconfiguration because it has a high accuracy and significant speed. The proposed method is simulated on a well-known distribution network. The achieved results were highly satisfactory and applicable.

Keywords— Reconfiguration; Probabilistic Loads; Distributed Generation; Distribution System.

I. INTRODUCTION

Nowadays, distribution systems are growing rapidly and get more complex. Due to the radial structure in almost all of distribution networks, consumers are fed just from one side. Since these networks are complex, there are different strategies to feed them, the best explanation is the presence of numerous switches in distribution networks which can change the structure of the network. Changes in the structure of network which is done by altering status of its switches is called reconfiguration, it not only determines the type of consumers feeding but it also has more applications, some of them include load balancing, minimizing total losses of system and improving voltage deviation.

Since there are a lot of switches in the network, reconfiguration issue is an optimization problem with some limitations. The most important limitations are keeping radial structure of network and consumers voltage deviation. Seeking for optimal structure of network, on the one hand, and its applicability, on the other, is very vital. In case the practical limitations are neglected, the optimal answer won't be acceptable.

Today, reconfiguration of distribution networks is an engineering challenge, because optimal solution is always taken into account and due to size and complexity of these problems, the only possible way is to employ specialized software. The main objective of optimization is to minimize expenses and to improve services. There has been so much research regarding reconfiguration problem and a lot of methods have been applied on it. Reconfiguration problem was first considered in (Merlin and Back, 1975) in order to minimize total losses by a heuristic and hybrid optimization algorithms. Changing the status of the switches can be carried out by various algorithms, but since power system problems are combinatorial optimization, they are difficult to be solved by traditional linear or nonlinear methods (Baran and Wu, 1989; Wu et al., 2010). Authors of recent literatures have used optimization methods such as genetic algorithm (GA), fuzzy systems, bee colony (BC), simulated annealing (SA), Tabu searches, heuristic algorithms, particle swarm optimization (PSO) etc. (de Macedo Braz and de Souza, 2011; Arun and Aravindhababu, 2010; Olamaeia et al., 2012; Jeon et al., 2010; Abdelaziz et al., 2010; Guedes et al., 2013; Ghandehari et al., 2013). Recently a new heuristic algorithm, which is also applied in the present study, has been introduced called "Sifting Algorithm" (Shojaeian and Ghandehari, 2013). It has some advantages including simple structure, high speed and accuracy.

The other issue in the reconfiguration problem is the objective function. The most important objective is loss minimization although there are more objectives to be considered such as reliability, voltage deviation, load balancing, transient behaviours of the network, smart grid interactions, etc. (Ghandehari et al., 2013; Shojaeian and Ghandehari, 2013; Sua et al., 2005; Saffar et al., 2011; Spitsa et al., 2012; Enacheanu et al., 2008; Georgilakis and Hatziargyriou, 2013; Fei and Loparo, 2013; Liu and Hsiao-Dong, 2013; Rao et al., 2013; Pavani and Singh, 2013; Moarrefi et al., 2013). One or two objectives are usually optimized simultaneously but occasionally more than two objectives are considered as optimization (Shojaeian and Ghandehari; 2013). This paper optimizes four objectives involving load balancing, total losses of network, voltage deviation and system reliability.

In a distribution system if it is assumed that loads are constant, reconfiguration will not be very hard, but obviously you know actual loads are not constant and always are changing. To resolve this problem it can be assumed that loads are stochastic. Other important issue is the presence of DGs which can affect reconfiguration of networks, since they change load flow paths. It is clear that a DG generated power depends on environmental conditions and so it is a probabilistic variable. Loads power and the generation of renewable wind energy resources are uncontrollable. These random parameters enter some additional unknown constituents in the calculations, which complicate and prolong the planning and analysis of the system. The loads and the wind speed during the year fluctuate, so in order to have a realistic evaluation, their probabilistic model is used.

To have a real answer and more practical reasons, the present study assumes that loads are probabilistic and 3 DGs (wind generators) have been placed in the distribution network. These two issues have so far been separately investigated; there are rare occasions, like the one in our study, in which the combinatory form is studied.

II. PROBABILISTIC MODEL OF LOADS

It is obvious that electrical loads have a probabilistic nature inherently. There are two prime parameters in power flow which lead to load change in network; i.e. time (daily, weekly, seasonal and annual profiles) and climate conditions. It should be noted that in deterministic power flow, these two parameters are ignored. In this paper a probabilistic daily load profile is used for each season.

If μ_PLj and μ_QLj are considered as the average active and reactive power of the j^th load and m is a probabilistic sample of time, average active and reactive power are defined as follows:

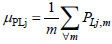	(1)
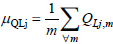	(2)

Further, the active and reactive power's variance is calculated as follows:

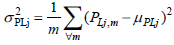	(3)
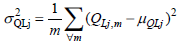	(4)

Considering the nature of the real loads, normal distribution function can be applied (Billinton and Allen, 1996). This distribution is defined as:

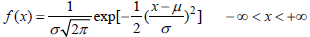(5)

Figure 1 shows standard deviations of normal distribution which is assumed to be in the vicinity of the deterministic loads values.

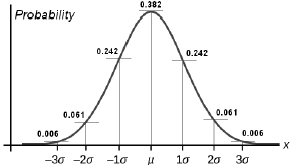
Fig. 1: Change of normal distribution to seven-deviation standard

III. PROBABILISTIC MODEL OF WIND SPEED AND DGs

The wind speed has a probabilistic nature. A prototype of wind speed can be figured out based on the previous statistical analysis (http://climate.weatheroffice.gc.ca). A model for daily change of wind in every season is applied in the present study. For probabilistic modelling of wind speed, Weibull distribution function is applied (Yingni et al., 2006). This function is formulized in Eq. (6).

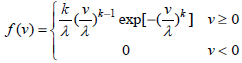(6)

Considering the average mean and speed deviation obtained from previous statistical sample, the coefficients k and λ in Weibull distribution could be calculated by the Eq. (7) and Eq. (8).

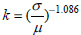	(7)
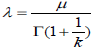	(8)

Figure 2 shows wind speed model with Weibull distribution in every season.

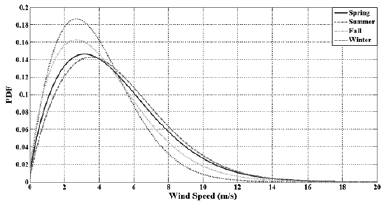
Fig. 2: Wind speed model with Weibull distribution in every season.

When wind speed is below or above a certain level, practically, the turbine is gotten out of the circuit; In high speeds, to prevent damaging turbine and gearbox, and in low speeds, for non-synchronization with the network; these limitations can be explained as follows (Hetzer et al., 2008; Fig. 3).

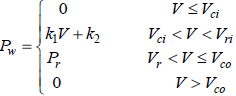	(9)
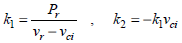	(10)

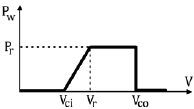
Fig. 3: Limitations for generation by wind turbine

where P_w is rated power of turbine, V_ci and V_co are minimum and maximum speed of wind for turbine (working win speed range) respectively and V_r is minimum speed of wind to generate a constant power (P_r).

In this paper, five wind Turbine (H19.5-100kw) in every wind farm, with aforementioned limitations, is applied (http://chinahummer.en.made-in-china.com):

P_r=100kW, V_ci=2.5m/s, V_r=12.5m/s, V_co=25m/s

IV. DG PLACEMENT

The optimal DGs placement is done by binary particle swarm optimization (BPSO) algorithm and through considering average loads consumption in the present study. Consider that three 500kw (5*100kw) wind turbine have been selected taking the nature of recommended network (Fig. 4). Figure 5 shows convergence curve of optimal placement of the DGs. Placement of these DGs are on buses 7, 12 and 16.

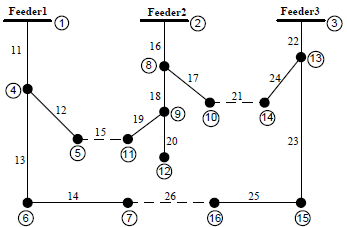
Fig. 4: Recommended distribution system

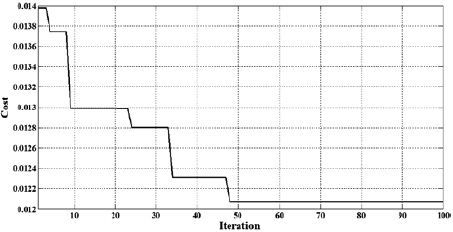
Fig 5: convergence curve of optimal placement

V. RECONFIGURATION METHOD

The first step to solve reconfiguration problem is the representation of the network structure. The status of each switch can be determined by 0 and 1 codes, for OPEN and CLOSED status respectively. Then to show the status of N switches in a distribution feeder, a string of N bits can be used. If the statuses of switches change, their string code will change as well. An optimum code for the network has to be found which results in minimum value of the objective function.

One advantage of the reconfiguration problem is its unfeasible solutions that are predictable, so search space can be reduced. There are different ways to determine feasible states, some of which have been introduced in (Ghandehari et al., 2013). By reducing search space of the problem, speed of program will increase to a large extent. When structures of the network have been determined, the best of them should be found. Artificial intelligence algorithms should be used for this purpose. Sifting algorithm is a suitable method and has been applied in the present study.

In the first step one feasible string is selected, the next step is to randomly select matrixes of buses and afterwards is to evaluate the objective function (via a fast and accurate forward/backward load flow method (Baran and Wu, 1989)). Remember that loads and DGs are probabilistic and when matrixes of buses are determined, one of their states should be selected randomly. Flowchart of Fig. 6 explains this method.

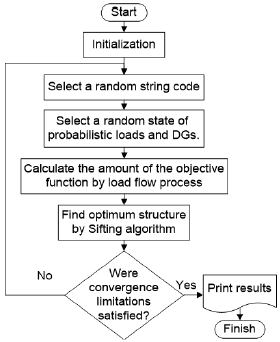
Fig. 6: Flowchart of the recommended method

At the present study PLs and DGs have been selected at 4 hours of a day (6, 12, 18 and 24). Every hour has 7 probabilistic states, so there are 24 states (7*4) in a day that should be verified.

VI. THE OBJECTIVE FUNCTION

The objective function (Cost) used in this paper has four weighted components including: load balancing (LB), total network losses (NL), voltage deviation (VD) and system reliability (SR). It is shown as following:

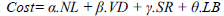(11)

That α, β, γ, and θ are the weighting coefficients which show relative importance of the components. These coefficients are obtained with historical experiences and strategies of each distribution system management. In this paper, with trial and error, these coefficients are chosen 1, 2, 0.0015 and 31 respectively. Total losses and voltage deviations will be obtained by (12) and (13).

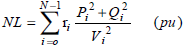	(12)
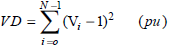	(13)

where V_i is the voltage magnitude of the i^th bus and P_i, Q_i, and r_i are the active and reactive power and resistance of the i^th section respectively.

In this paper reliability of distribution networks are taken into account by system reliability indices. For each load center an average failure rate (λ in #/year), an average repair time (r in hours), and an average outage time (U in hours/year) can be calculated (Billinton and Allen, 1996), where:

U = λ.r

(14)

The system reliability indices used in this paper are System Average Interruption Frequency Index (SAIFI) and System Average Interruption Duration Index (SAIDI). They can be obtained by Eq. (15) and Eq. (16):

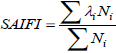	(15)
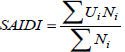	(16)
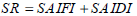	(17)

where N_i is the number of customers at the i^th load center. Moreover, one can consider different weighting factor (γ₁ and γ₂ instead of γ) for SAIFI and SAIDI. Reliability parameters for considered system are listed in the paper appendix.

Load balancing component will be obtained by Eq. (18). I_i is total current magnitude of the i^th feeder section.

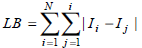(18)

VII. SIMULATION AND RESULTS

In previous sections all parts of a reconfiguration process have been introduced and now a practical program should be written. These parts include load flow, PLs, probabilistic DGs, reconfiguration and objective function. Table 1 shows reconfiguration results for the distribution network which is shown in Fig. 4 and Fig. 7 shows the convergence diagram of the objective function. Consequently Fig. 8 shows voltage profile of buses before and after reconfiguration.

Table 1: Results of reconfiguration

* This time is the average of 10 runs on a core 2 Duo 2.2GHz PC.

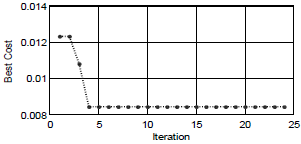
Fig. 7: Convergence diagram of a random run.

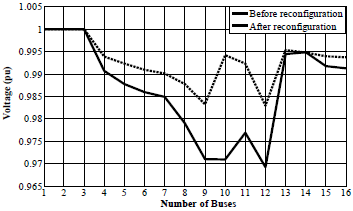
Fig. 8: voltage profile of buses

VIII. CONCLUSION

In the present paper, a well-known 13-bus distribution system including PLs and DGs has been reconfigured considering suitable probabilistic models. The Sifting algorithm has been used to reconfigure the network, because it characterizes with high accuracy and speed. Results are very satisfactory and CPU time shows that this method can be practical for very large distribution networks.

APPENDIX

Reliability parameters for considered system are:

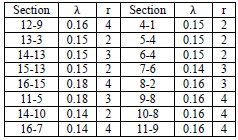REFERENCES
1. Abdelaziz, A.Y., F.M. Mohamed, S.F. Mekhamer and M.A.L. Badr, "Distribution system reconfiguration using a modified Tabu Search algorithm," Electric Power Systems Research, 80, 943-953 (2010).
2. Arun, M. and P. Aravindhababu, "Fuzzy based reconfiguration algorithm for voltage stability enhancement of distribution systems," Expert Systems with Applications, 37, 6974-6978 (2010).
3. Baran, M.E. and F.F. Wu, "Network reconfiguration in distribution systems for loss reduction and load balancing," IEEE Transactions on Power Delivery, 4, 1401-1408 (1989).
4. Billinton, R. and R.N. Allan, Reliability Evaluation of Power Systems, Second Edition, Plenum Press, New York (1996).
5. De Macedo Braz, H.D. and B.A. de Souza, "Distribution network reconfiguration using genetic algorithms with sequential encoding: Subtractive and additive Approaches," IEEE Transactions on Power Systems, 26, 582-593 (2011).
6. Enacheanu, B., B. Raison, R. Caire, O. Devaux, W. Bienia and N. Hadj Said, "Radial Network Reconfiguration Using Genetic Algorithm Based on the Matroid Theory," IEEE Transactions on Power Systems, 23, 186-195 (2008).
7. Fei, D. and K.A. Loparo, "Network reconfiguration analysis with the consideration of distributed generation," IEEE Energytech, 1-5 (2013).
8. Georgilakis, P.S. and N.D. Hatziargyriou, "Optimal Distributed Generation Placement in Power Distribution Networks: Models, Methods, and Future Research," IEEE Transactions on Power Systems, 28, 3420-3428 (2013).
9. Ghandehari, E., S. Shojaeian and J. Pourabadeh, "An Improved Multi-Objective Bpso-Based Method for Radial Distribution Networks Reconfiguration," Journal of Siberian Federal University. Engineering & Technologies, 6, 617-624 (2013).
10. Guedes, L.S.M., A.C. Lisboa, D.A.G. Vieira and R.R. Saldanha, "A Multiobjective Heuristic for Reconfiguration of the Electrical Radial Network," IEEE Transactions on Power Delivery, 28, 311-319 (2013).
11. Hetzer, J., D.C. Yu and K. Bhattarai, "An economic dispatch model incorporating wind power," IEEE Transactions on Energy Conversion, 23, 603-611 (2008).
12. Jeon, Y.J., J.O. Kim, J.R. Shin and K.Y. Lee, "An efficient simulated annealing algorithm for network reconfiguration in large-scale distribution systems," IEEE Transactions on Power Delivery, 17, 1070-1078 (2002).
13. Liu, J. and C. Hsiao-Dong, "Maximizing delivery capability of unbalanced distribution networks for high penetration of distributed generation," IEEE Power and Energy Society General Meeting, 1-5 (2013).
14. Merlin, A. and H. Back, "Search for minimum-loss operating spanning tree configuration in an urban power distribution system," 5th Power System Computation Conference (1975).
15. Moarrefi, H., M. Nematollahi and M. Tadayon, "Reconfiguration and distributed generation (DG) placement considering critical system condition," Electricity Distribution, (CIRED 2013), 1-4 (2013).
16. Olamaeia, J., T. Niknamb and S. Badali Arefia, "Distribution Feeder Reconfiguration for Loss Minimization Based on Modified Honey Bee Mating Optimization Algorithm," Energy Proceeding, 14, 304-311 (2012).
17. Pavani, P. and S.N. Singh, "Reconfiguration of radial distribution networks with distributed generation for reliability improvement and loss minimization," IEEE Power and Energy Society General Meeting, 1-5 (2013).
18. Rao, R.S., K. Ravindra, K. Satish and SV.L. Narasimham, "Power Loss Minimization in Distribution System Using Network Reconfiguration in the Presence of Distributed Generation," IEEE Transactions on Power Systems, 28, 317-325 (2013).
19. Saffar, A., R. Hooshmand and A. Khodabakhshian, "A new fuzzy optimal reconfiguration of distribution systems for loss reduction and load balancing using ant colony search-based algorithm," Applied Soft Computing, 11, 4021-4028 (2011).
20. Shojaeian, S. and E. Ghandehari, "A Heuristic Multiobjective Method for Radial Distribution Networks Reconfiguration," Chinese Journal of Engineering, Article ID 654074 (2013).
21. Spitsa, V., X. Ran, R. Salcedo, J.F. Martinez, R.E. Uosef, F. de Leon, D. Czarkowski and Z. Zabar, "On the Transient Behavior of Large-Scale Distribution Networks During Automatic Feeder Reconfiguration," IEEE Transactions on Smart Grid, 3, 887-896 (2012).
22. Sua, C.T., C.F. Changb and J.P. Chiouc, "Distribution network reconfiguration for loss reduction by ant colony search algorithm," Electric Power Systems Research, 75, 190-199 (2005).
23. Wu, Y.K., C.Y. Lee, L.C. Liu and S.H. Tsai, "Study of Reconfiguration for the Distribution System With Distributed Generators," IEEE Transactions on Power Delivery, 25, 1678-1685 (2010).
24. Yingni, J., Y. Xiuling, C. Xiaojun and P. Xiaoyun, "Wind potential assessment using the Weibull model at the Inner Mongolia of China," Energy Exploration and Exploitation, 24, 211-221 (2006).

Received: March 15, 2014.
Accepted: October 16, 2014.
Recommended by Subject Editor: Jorge Solsona.