Servicios Personalizados
Articulo
Latin American applied research
versión On-line ISSN 1851-8796
Lat. Am. appl. res. vol.45 no.2 Bahía Blanca abr. 2015
Theoretical analysis of overlaid cement concrete pavement with crack
Y. Gao
College of Civil Engineering and Mechanics, Yan Shan University, Qinhuangdao Hebei 066004, China. Gaoyuanyuan2286@163.com
Abstract— In this paper, overlaid Portland cement concrete (PCC) with crack subjected to vehicle load is considered based on theoretical analysis. In order to build efficient model, PCC is reduced to an elastic plate on Winkler foundation. Fourier integral transform, residue theorem and Lobatto-Chebyshev integration formula are used to obtain the analytical solutions on the stress and strain fields of the pavement and stress intensity factors of the crack tip. Stress intensity factors are numerically calculated. The stress intensity factors of the crack tips(b) in the pavement with 10cm thickness overlay are reduced heavily, especially for I type crack. Overlay thickness is very significant factor that effect the value of stress intensity factor of I type crack, rather than II type crack. However, stress intensity factors are less affected by elastic modulus of overlay material.
Keywords— Cement Concrete Pavement; Crack; Pavement Overlay; Fracture Mechanics; Stress Intensity Factor.
I. INTRODUCTION
Portland cement concrete (PCC) is a common structure of pavement. Because of traveling load, seasonal temperature variations, shrinkage or chemical attack of cement concrete and so on, the damages in the form of cracks could be induced in the cement concrete pavement. It badly influences the safety and comfort of driving. The most common rehabilitation technique for deteriorated concrete pavement is the placement of an asphalt overlay on top of it. However, the reflection cracks always occur and reduce the service life of asphalt overlay. Therefore, the causes of the problems have to be well settled at the design stage.
Some experts have implemented several methods to mitigate the development of reflection cracks. Most research began at 1990's and focused on finite element method (Liu and Wang, 2011; Baek, 2010) and experiment al study (Kim and Nelson, 2004; Doh et al.,2009; Li et al.,2014). Ghauch and Abou-Jaoude (2013) researched reflective cracks which appeared in asphalt overlays placed on top of a concrete pavement. Their papers research the effects of sub-grade and sub-base strengths, vehicle speed, overlay thickness, and pavement temperature to identify the parameters that deteriorate the overlay. Wu et al. (2014) developed a pavement crack propagation analysis tool, neural networks based on semi-analytical finite element analysis, to calculate the stress intensity factors (SIFs) at the crack tip for pavement crack propagation analysis. Qian et al. (2013) introduced Engineered Cementitious Composite which can extend the service life of pavement overlay with less thickness compared with concrete overlay proved by experimental testing on fatigue performance of ECC. Increasing the overlay thickness, rubblizing the concrete pavement, and placing stress relieving interlayer systems or geosynthetics (Khodaii et al., 2009; Kim and Buttlar, 2002) were adopt to alleviate the reflection crack.
Up to now, the problem of reflection cracks occurring shortly after pavement rehabilitation is still an issue for pavement designers and road managers. Thereby, theoretical analysis of overlaid cement concrete pavement with crack for understanding the mechanism of cracks propagation is still needed. Compared with the finite element method, the computational accuracy of the theoretical method is better. It can provide advices for pavement design and helpful for developing finite element software. In this paper, theoretical analysis of cement concrete pavement with an asphalt overlay based on fracture mechanics is conducted. In order to identify the parameters involved in the role of the overlay, the effects of load position, crack length, overlay thickness, and elastic modulus of overlay are investigated.
II. DESCRIPTION OF THE PROBLEM
Overlaid PCC with crack subjected vehicle load is considered as a plate on an elastic foundation shown in Fig. 1.
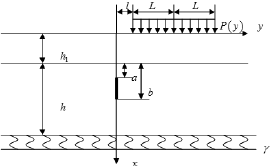
Fig.1. Model of cement concrete pavement with overlay containing crack
In Fig. 1, h is thickness of old cement concrete pavement, h1 is thickness of overlay, x is depth direction of pavement, γ is longitudinal direction of pavement, g is foundation modulus, P(y) is vehicle load, L is range of load and l is horizontal distance between edge of vehicle load and crack. The crack emerges on the surface of the old concrete pavement as a=h1. In this study, only the plane strain is concerned, thus the effect of volume force is ignored.
In order to simplify the problem shown in Fig. 1, based on the linear-elastic superposition principle, the problem can be presented by three sub-models. The three sub-models are shown in Fig. 2, Fig. 3 and Fig. 4 respectively.
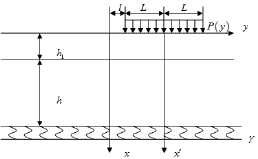
Fig.2. The first sub-problem
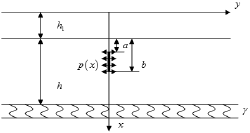
Fig.3. The second sub-problem
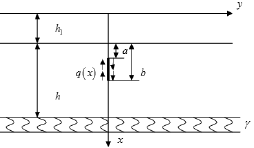
Fig.4. The third sub-problem
III. SOLUTION OF p(x) AND q(x) IN SUB-PROBLEM 1
In sub-problem 1, in order to simplify this problem, coordinate translation method is adopted. The y coordinate axis is moved l+L units to the right and the model is reduced to a plane strain problem with a symmetric load vertical to the boundary. According to theory of linear-elastic superposition, p(x) and q(x) in sub-problem 2 and sub-problem 3 can be expressed in the following forms:
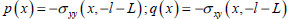 | (1) |
IV . SOLUTION OF IN SUB-PROBLEM 2
The boundary conditions of sub-problem 2 shown in Fig. 3
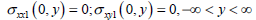 | (2) |
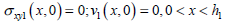 | (3) |
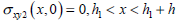 | (4) |
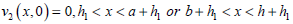 | (5) |
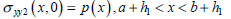 | (6) |
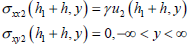 | (7) |
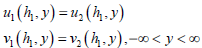 | (8) |
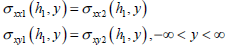 | (9) |
where σxxn and σyyn are the x and y components of the stress vector in layer n, respectively, σxyn is the shearing stress in layer n, un and vn are the x and y components of the displacement vector in layer n (n=1,2), respectively. n=1 presents the overlay and n=2 presents the old cement concrete pavement. γ is the stiffness of the foundation.
The governing equations of plane elasticity can be expressed as (Li, 2000):
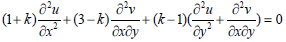 | (10) |
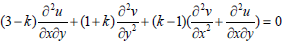 | (11) |
where k=(3-v)/(1+v) for plane stress, k=3-4v for plane strain and v is Poisson's ratio. In this paper, k=3-4v is selected corresponding to the case of plane strain.
In order to achieve the solutions of governing Eqs. (10) and (11), Fourier transform and inverse Fourier transform can be used. One can obtain the expressions of displacements un and vn as:
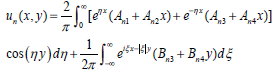 | (12) |
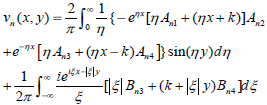 | (13) |
where Bn3 and Bn4 are the functions of ξ and An1, An2, An3 and An4 are the functions of η.
Substituting Eqs. (15) and (16) into Hooke's Law, the components of stress are given by:
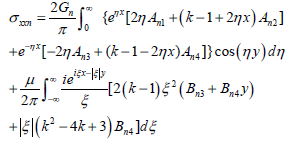 | (14) |
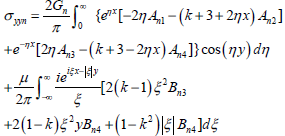 | (15) |
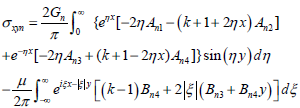 | (16) |
In this problem, v1= v2 = v is assumed for their approaching value and Gn is the shear modulus in layer n.
For convenience, considering the equation defining this (Kadioğlu et al.,1998):
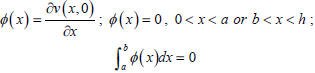 |
The function, ø(x), is a component of deformation gradient (Fig. 3) along the crack surface, and then An1, An2, An3, An4, Bn3, Bn4 (n=1,2) can be expressed by dislocation density function.
Based on Eqs. (3) and (4) and the theory of residue, B13, B14, B23 and B24 are expressed respectively as:
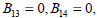 | |
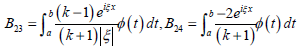 | (17) |
Based on Eqs. (2), (7)-(9), inverse Fourier transform and residue theorem, A11,A12, A13, A14, A21, A22, A23 and A24 can be expressed by ø(t).
Substituting A21, A22, A23, A24, B23 and B24 into the boundary condition Eq.(6) , it yields:
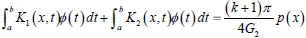 | (18) |
In Eq. (18), 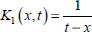 .
.
To solve the integral equation numerically by using a collocation technique, the interval (a, b) in Eq. (18) is normalized and expressed as:
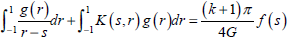 | (19) |
Lobatto-Chebyshev integration formula is then used to solve the singular integral equations. The singular integral equation is converted to a system of linear equations by means of this numerical method. The expression of Eq. (19) can be written as:
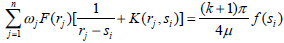 | (20) |
In Eq. (20), there are n-1 equations and the last equation comes from the property of dislocation density function which is expressed as 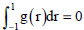 for the embedded crack. It is also written as:
for the embedded crack. It is also written as:
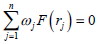 | (21) |
where ωj is the weight function
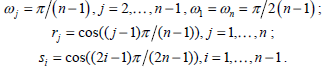 |
The stress intensity factors are defined and evaluated as (Kadioğlu,1998):
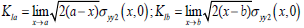 | (22) |
Substituting the numerical solution into Eq. (22), one can obtain:
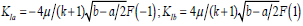 | (23) |
V. SOLUTION OF KII IN SUB-PROBLEM 3
The same method applied for second sub-problem can also be used to solve the model shown in Fig. 4 and the stress intensity factors can be express:
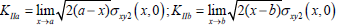 |
VI. ANALYSIS OF CALCULATION EXAMPL E
In order to evaluating the efficacy of overlay for resisting crack propagation, stress intensity factors of crack tips in old PCC are calculated with and without overlay. To identify the parameters involved in the role of the overlay, different thickness and shear modulus of the overlay are selected for calculating the stress intensity factors of crack tip. The results are shown in Tables 1-2 and Figure 5-8.
Table 1: Comparison of stress intensity factors KIb with and without overlay units 103N/m(3/2)
Table 2: Comparison of stress intensity factors KIIb with and without overlay units 103N/m(3/2)
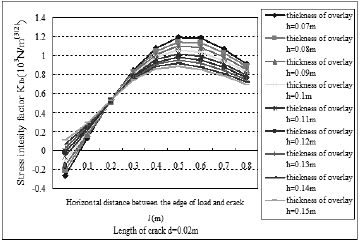
Fig.5. Result of stress intensity factor KIb of the crack tips (b) with different thickness.
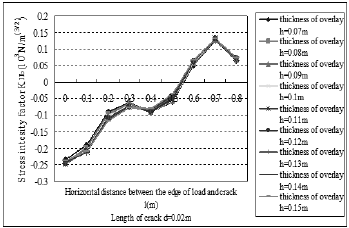
Fig.6. Result of stress intensity factor KIIb of the crack tips (b) with different thickness.
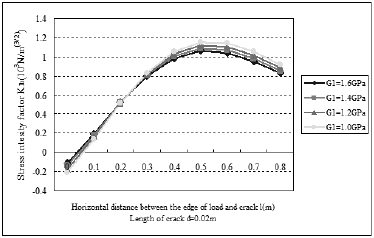
Fig.7. Result of stress intensity factor KIb of the crack tips (b) with different shear modulus of overlay.
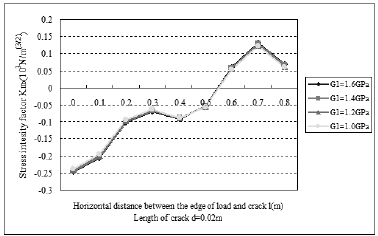
Fig.8. Result of stress intensity factor KIIb of the crack tips (b) with different shear modulus of overlay.
The parameters for model 1 are P=700000 N/m, L=0.15m, E1=4.32×109 N/m2, G1=1.6×109 N/m2, h1=0.1 m, v1=0.35, k1=1.6, E2=3.1×1010 N/m2, G2=1.1482×1010 N/m2, γ=1.3×109 N/m3, h2=0.25 m, v2=0.35, k2=1.6, a=h1, d=b-a, β= G2/γ=8.832.
Table 1 and Table 2 show, no matter I type crack or II type crack, the stress intensity factors of the crack tips (b) in the pavement with overlay are smaller than that in pavement without overlay. Furthermore, the values of stress intensity factors of I type crack tips (b) in the pavement with overlay are reduced to approximate 50% of without overlay, with the same load position and identical crack length. It indicates that using the overlay is an effective way for lowering the crack extension.
Figure 5 and Fig. 6 show, with the thickness of the overlay increasing from 7cm to 15cm, the stress intensity factors of I type crack decrease slightly, while the stress intensity factors of II type crack do not presence obvious change. Therefore, it is not wise choice to increase the thickness of overly directly. Grid or other Geosynthetic could be considered as a Interlayer to reinforce on mitigating reflection cracking in asphalt over lays and theoretical analysis of these structure will be conducted in the later research.
From the 4 overlapping curves almost in Fig. 8, with the increasing of shear modulus of overlay from 1.0GPa to 1.6GPa, the stress intensity factors of II type crack have not change. In Fig. 7, stress intensity factors of I type crack are decreased slightly as the shear modulus of overlay increase, while the horizontal distance between the edge of load and crack exceed 0.25m. It denotes that the shear modulus of overlay is not a significant factor that influences the crack propagation in old cement concrete pavement and it is not appropriate method to improve the effect of overlaying by changing the overly modulus.
VII. CONCLUSIONS
Based on the theory of fracture mechanics, the model of concrete pavement with an overlay is built as it is reduced to an elastic plate on Winkler foundation. Method of Fourier transform and dislocation density function in association with solving the singular integral equations are introduced to calculate the stress and stress intensity factors in PCC pavement which contains a crack perpendicular to the interface and with asphalt overlay on it. This method can be used to analyze effect of asphalt overlay for resisting crack propagation. Current numerical simulation indicates that the asphalt overlay on top of the old concrete pavement plays an important role for protecting the structure from the crack damage. The thickness and the shear modulus of the overlay are not the two significant factors that affect the overlay.
REFERENCES
1. Baek, J., Modeling reflective cracking development in hot-mix asphalt overlays and quantification of control technique, Ph.D. Dissertation, University of Illinois at Urbana- Champaign (2010).
2. Doh, Y.S., S.H. Baek and K.W. Kim, "Estimation of relative performance of reinforced overlaid asphalt concretes against reflection cracking due to bending more fracture," Construction and Building Materials, 23, 1803-1807 (2009).
3. Ghauch, Z.G. and G.G. Abou-Jaoude, "Strain response of hot-mix asphalt overlays in jointed plain concrete pavements due to reflective cracking," Computers and Structures, 124, 38-46 (2013).
4. Kadioğlu, S., S. Dağ and S. Yahsi, "Crack problem for a functionally graded layer on an elastic foundation," International Journal of Fracture, 94, 63-77 (1998).
5. Khodaii, A., S. Fallah and F.M. Nejad, "Effects of geosynthetics on reduction of reflection cracking in asphalt overlays," Geotextiles and Geomembranes, 27, 1-8 ( 2009).
6. Kim, J. and W.G. Buttlar, "Analysis of Reflective Crack Control System Involving Reinforcing Grid over Base-Isolating Interlayer Mixture," Journal of Transportation Engineering, 128, 375-384 (2002).
7. Kim, S.M. and P.K. Nelson, "Experimental and numerical analyses of PCC overlays on PCC slabs-on-grade subjected to climatic loading," International Journal of Solids and Structures, 41, 785-800 (2004).
8. Li, S., X.W. Liu and Z.H. Liu, "Interlaminar shear fatigue and damage characteristics of asphalt layer for asphalt overlay on rigid pavement," Construction and Building Materials, 68, 341-347 (2014).
9. Li, Y.D., Theory and application of fracture mechanics, Science press, Beijing (2000).
10. Liu, K. and F. Wang, "Computer Modeling Mechanical Analysis for Asphalt Overlay under Coupling Action of Temperature and Loads," Advanced in Control Engineering and Information Science, 15, 5338-5342 (2011).
11. Qian, S.Z., V.C. Li, H. Zhang and G.A. Keoleian, "Life cycle analysis of pavement overlays made with Engineered Cementitious Composites," Cement & Concrete Composites, 35, 78-88 (2013).
12. Wu, Z.H., S. Hu and F.J. Zhou, "Prediction of stress intensity factors in pavement cracking with neural networks based on semi-analytical FEA," Expert Systems with Applications, 41, 1021-1030 (2014).
Received: July 21, 2014.
Accepted: November 5, 2014.
Recommended by Subject Editor: Walter Tuckart.