Fuentes de incertidumbre, probabilidades condicionales y la opción de abandono en activos reales

Sources of uncertainty, conditional probabilities and the abandonment option for real assets

Gastón S. Milanesi^a

^a Departamento de Ciencias de la Administración, Universidad Nacional del Sur. E-mail: milanesi@uns.edu.ar.

Fecha de recepción: 27/07/2010
Fecha de aceptación: 06/10/2011

Resumen
Las opciones reales cuantifican el valor de la flexibilidad estratégica de una inversión, siendo el modelo binomial la herramienta para su valoración. Con varias fuentes de incertidumbre sobre el valor del activo real el modelo es polinomial. El trabajo propone un método para estimar el valor de la flexibilidad estratégica de una inversión con múltiples fuentes de incertidumbre. Los principales puntos son: (a) introducción del enfoque de opciones reales y las herramientas de valoración: rejillas binomiales y multinomiales, (b) insumos para el tratamiento de la incertidumbre, construcción de rejillas y valoración de las opciones: Teorema de Bayes, Movimiento Geométrico Browniano y equivalentes ciertos, (c) marco operativo de cinco pasos para la implementación del método de valuación. Caso de aplicación: valoración de la opción de abandono (venta a los competidores) de un proyecto de investigación y desarrollo (R&D) suponiendo correlación e independencia entre las variables estocásticas (ingresos y costos).

Palabras clave: Opciones reales; Rejillas multinomiales; Teorema de Bayes; Movimiento Geométrico Browniano; Probabilidades condicionales.

Abstract
The real options approach captures the strategic flexibility of the investment in real assets, being the binomial model the tool for its valuation. Whit various sources of uncertainty about the value of the real asset, the model is polynomial. This paper proposes a framework for value the strategic flexibility of an investment with many sources of uncertainty. The main points are: (a) introduction of the real options approach and the valuation tools: binomial and multinomial lattice, (b) inputs for the treatment of the uncertainty, building lattice and real options valuation: Bayes' Theorem, Geometric Brownian Motions and certain equivalents, (c) overall framework of five steps for the implementation of the valuation method: Case of application: valuation of the abandonment option on a research and development project (R&D); assuming correlated and uncorrelated stochastic variables (incomes and costs).

Key words: Real options; Multinomial lattices; Bayes' Theorem; Geometric Brownian Motion; Conditional probabilities.

JEL: C44, G13, G30

1. Valuación de activos y el enfoque de Opciones Reales

Uno de los métodos de valuación de activos reales de mayor difusión y uso, destinado a cuantificar el valor intrínseco de la inversión, es el descuento de flujos de fondos (DFF) y sus diferentes variantes¹. Bajo esta metodología de valuación los beneficios y costos asociados a un proyecto son actualizados empleando una tasa ajustada por el riesgo representativo de la inversión evaluada. El valor actual de los flujos de fondos se adiciona y a posteriori se sustrae el costo de la inversión, con el objeto de determinar la contribución marginal a la riqueza de la firma y del propietario de los fondos. Sin dejar de conocer el importante uso de esta herramienta a la hora de estimar el valor de un activo real, una de las principales debilidades consiste en que el método supone irreversibilidad de la inversión. Esto implica que la flexibilidad estratégica y táctica producto del dinámico gerenciamiento de la decisión de inversión no es capturada por el tradicional enfoque de descuento de flujos de fondos, (Dixit y Pindyck, 1994; Trigeorgis, 1997; Mun, 2004).

La Teoría de Opciones Reales (OR) ofrece un complemento al DFF, ya que considera la variabilidad vinculada al dinamismo derivado de la ejecución y concreción de las metas y objetivos propios de la inversión. El enfoque de OR nace como adaptación del modelo de valoración de opciones financieras de Black y Scholes (1973); Merton (1973) para capturar la flexibilidad estratégica de inversiones en activo reales. La primera propuesta es desarrollada por Myers (1977) a partir de la opción de crecimiento. En la literatura se pueden encontrar diferentes propuestas analíticas para el tratamiento de categorías específicas de opciones, entre ellos: (a) Opción de Diferimiento (Mc Donal y Siegel, 1986); (Paddock, Siegel y Smith, 1988); (Ingersoll y Ross, 1992); (b) Opción de Crecimiento (Myers, 1977); (Pindyck; 1988); (Trigeorgis, 1988); (Smit, 1996); (c) Opción de Abandono (Myers y Majd, 1990); (d) Opciones de expandir-contraer o extensión de la vida útil (Trigeorgis y Mason, 1987); (Kemma, 1988); (e) Opción de cierre temporario o corte del proceso productivo (Brennan y Schwartz, 1985a , 1985b); (f) Opción de intercambio (Margrabe, 1978); (Kulatilaka, 1988, 1995); Opciones financieras de insolvencia (Mason y Merton, 1985); (Trigeorgis, 1993).

La resolución analítica de las opciones de una inversión se instrumenta mediante ecuaciones diferenciales estocásticas (tiempo continuo) o discretamente a través del uso de árboles o grillas binomiales (Cox y Ross, 1976); (Luherman, 1998a) y (Hull, 2005). Paralelamente el enfoque de opciones reales se complementa con el análisis de decisiones incorporando tópicos como: riesgos de mercado y riesgos privados (sistemáticos y asistemáticos) (Smith y Nau, 1995); inexistencia completa de activos financieros replicantes y el enfoque (MAD; Marketed Asset Disclaimer; (Copeland y Antikarov, 2001) y (Copeland y Tuffano, 2004) y Opciones Reales y Teoría de Juegos (RO y Games Theory; (Trigeorgis y Smit, 2006).

Una complejidad adicional emerge cuando las fuentes de incertidumbre son varias, en este caso no basta con construir una única cartera que replique la volatilidad del proyecto empleando un activo financiero "gemelo" o replicante (twin security). Es condición necesaria estimar la volatilidad de las fuentes de incertidumbre y a posteriori, desarrollar métodos analíticos para resolver los sistemas de ecuaciones destinados a valuar los riesgos de la inversión.

En base a lo expuesto el objetivo del presente trabajo consiste en proponer un marco operativo e instrumental consistente de cinco pasos para resolver la valuación de la flexibilidad estratégica derivada contenida en el valor del proyecto. Para ello se propone trabajar con el enfoque de OR a través de grillas multinomiales y el método de equivalentes ciertos. Este modelo fue propuesto originalmente por Boyle, Evine y Gibbs (1989); Copeland y Antikarov (2001) y Brandao y Dyer (2009). La metodología propuesta es aplicable para los casos de independencia como de correlación entre las fuentes de incertidumbres vinculadas al activo real, siendo apropiada cuando las variables aleatorias siguen un proceso estocástico geométrico browniano. El marco teórico se complementa con la aplicación del método a un caso sobre un proyecto de investigación y desarrollo de productos (R&D) con opción de abandono (venta del proyecto a competidores) durante el estadio de desarrollo.

2. Las grillas binomiales y multinomiales

Las fuentes de incertidumbres que gobiernan y explican los valores esperados de los activos reales por lo general son múltiples. En estos casos al ser empleado el enfoque OR se está frente una tipología de opciones denominada arco iris ("rainbow options"). En las situaciones donde la incertidumbre es singular y; suponiendo que el proceso estocástico del activo responde a un movimiento Browniano, la resolución analítica del valor de la inversión en tiempo discreto requiere simplemente del empleo de grillas binominales. Caso contrario se deben apelar a un enfoque multinomial condicionado a si existe o no correlación entre las variables estocásticas.

Las grillas y árboles de decisión devengan el mismo resultado no obstante las grillas son operativamente más sencillas de trabajar, sobre todo a medida que se incrementa el número de periodos. Las grillas binomiales, a diferencia de los árboles, son más simples computacionalmente e intuitivas. La primera al representar el problema de manera compacta es más simple de interpretar; ya que el árbol tiene mayor información redundante en su recorrido (repite la misma probabilidad en varios lugares y estados equivalentes son representados en varios lugares).

Para re combinar en árboles se debe identificar estados de la naturaleza (en este caso distintos valores del proyecto sin opciones) donde las futuras probabilidades y flujos se condicionan al estado actual; pero no al camino tomado para llegar a dicho estado. Las grillas ofrecen una capacidad de recombinación compacta. De hecho si se comparan la cantidad de puntos finales y nodos entre una grilla binomial y un árbol se tiene:

1. Puntos finales grilla binomial: el número de puntos finales es igual al número de periodos (un proyecto con n=10 sus puntos finales asciende a n=11, ya que se comienza contando desde 0 al ser considerado un periodo más).
2. Nodos de decisión grilla binomial: el número total de nodos decisorios es igual a n(n+1)/2 (para el caso de 10 periodos se tienen, adicionando el inicial, 11*(11+1)/2=66)
3. Puntos finales árbol binomial: tiene un número de puntos finales igual a 2^n-1(para el caso de 10 periodos, contando desde el inicial, se tienen 2^11-1= 1024)
4. Nodos de decisión árbol binomial: tiene un número de nodos igual a 2ⁿ-1 (para el caso de 10 periodos, se tiene un total de 2¹¹-1= 2047)

Claramente se puede apreciar que el empleo de grillas es computacionalmente factible mientras que los árboles requieren algoritmos de resolución más complejos. De hecho este inconveniente de los árboles guarda directa relación con el número de periodos en consideración (ya sea por un incremento en los años o disminución de la amplitud del intervalo). Se argumenta que cuando se valúan opciones financieras los practicantes trabajan con no más de 30 intervalos, ya que una grilla tiene 465 nodos y el árbol de decisión contiene dos mil millones de nodos 2³¹-1=2.147.483.647 (Hull, 2005:206)

2.1. Generalización para grillas binomiales. El Triángulo de Pascal

En un esquema binomial, el valor del subyacente será una sucesión de estados buenos (u) y malos (d) a partir de su valor inicial (S₀). Para dos periodos esa misma sucesión se observará en las probabilidades del estado bueno (q) y malo (1-q); tal que: (borde superior; 1) S₀xu²xd⁰ => (q²x1-q⁰); (recombinación; 2) S₀x u¹*d¹ => (q¹x1-q¹); (borde inferior; 1) S₀xu⁰xd² => (q⁰*1-q²)1 (Milanesi y Vigier, 2010).

No obstante, en los estados intermedios cabe más de una posibilidad de arribar al estado final. En una grilla, a diferencia de un árbol, es fácil advertir en estos casos más de un camino o trayectoria para arribar a estados intermedios. En un ejemplo de dos períodos existen dos formas de arribar al estado final S₀x u¹xd¹. Un camino sería el estado malo en el primer período seguido del estado bueno en el segundo y viceversa. Por ello, la probabilidad asociada al estado intermedio, es la suma de las probabilidades de estas dos trayectorias. Por lo tanto en el modelo de dos períodos, el estado intermedio S₀x u¹xd¹, le corresponde una probabilidad (q¹x1-q¹) x 2².

En un problema con mayor número de períodos, la dificultad residiría en determinar la cantidad de veces que se repite la probabilidad; o dicho en otros términos, la cantidad de caminos o trayectorias para arribar a los estados intermedios (también llamados estados recombinantes). Una primera forma de resolver esta dificultad sería en reproducir la grilla y contar el número de trayectoria para arribar a cada estado final. Existe una herramienta matemática que facilita dicha tarea: el triángulo de Pascal³. Para definir los valores en cada elemento que compone el triángulo se sigue la siguiente regla:

1. Los valores extremos son iguales a uno,
2. Los valores intermedios en cada columna se definen como la suma de los valores en los extremos de la columna precedente.

La cantidad de combinaciones se obtiene de la siguiente manera: En la ilustración 1 si se toma como ejemplo el cuarto período surgen cinco estados finales (T+1), los cuales se reconocen por los cinco elementos de la columna correspondiente al cuarto período. El tercer estado del gráfico refleja las seis trayectorias que arriban a ese nodo. Dicho valor surge de sumar los valores indicados en la tabla, correspondiente a la columna anterior; o sea (3 + 3 = 6).

Ilustración 1: Triángulo de Pascal.

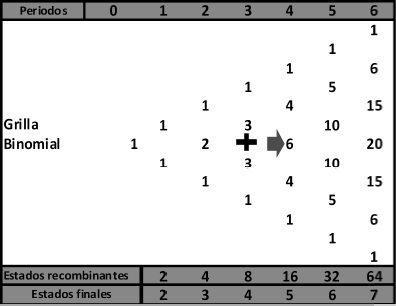
Fuente: Elaboración propia.

Los números del triángulo de Pascal coinciden con los números combinatorios. El número combinatorio C^m _n se encuentra en el triángulo en la fila n+1, en el lugar m+1. A la fórmula de los números combinatorios se le puede dar el carácter de fórmula general del triángulo para saber, sin necesidad de construir todas las filas anteriores, cuál es el número que ocupa un lugar determinado,

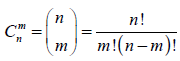Ecuación 1

Con el recurso del triángulo de Pascal se puede retornar al intento de generalizar el enfoque. La ilustración 2 ejemplifica los diversos estados de una grilla binomial para una opción de tres intervalos de tiempo.

Ilustración 2: Rejilla con proceso estocástico binomial.

Fuente: Elaboración propia.

La forma general que corresponde a cada elemento de la grilla precedente está representada por la siguiente expresión

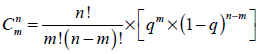Ecuación 2

En este caso n son los períodos y m los movimientos ascendentes. El primer término del producto, representa nuevamente la cantidad de trayectorias para arribar a cada estado intermedio (elemento del triángulo de Pascal).

Suponiendo que la opción sólo se ejerce en el período final (opción europea) y que su precio de ejercicio es representado por X; el valor actual de la opción OR₀ es igual al valor actual del valor esperado de los valores intrínsecos (VA [VE(VI(S_T))]). La forma general de la ecuación de valoración de opciones es;

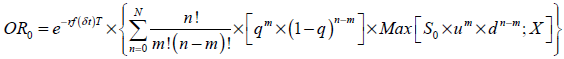Ecuación 3

2.2. El enfoque multinomial (polinomial)

Cuando existen más de dos resultados posibles según el estado de la naturaleza, la distribución de probabilidad recibe el nombre de multinomial. Esta es un caso general de la distribución binomial, con la particularidad de que en lugar de tener dos posibles resultados existen n posibles resultados (Mood y Graybill, 1978). Supóngase que existen k resultados posibles de un suceso aleatorio. Si fuesen dos resultados (binomial) la suma de las probabilidades es igual a q + (1-q)=1. Al ser multinominal se debe verificar que . Si el suceso se repite n veces y x₁ representa la cantidad de oportunidades que se genera q₁; x₂ la cantidad de veces que se verifica q₂ y así sucesivamente, la función es planteada de la siguiente manera;

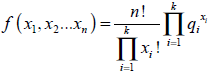Ecuación 4

Se trata de una distribución multivariante con k parámetros; n, q₁; q₂ ;q_3....q_k-1 . La otra variable (el complemento de q); como en el caso de la distribución binomial, se determina por diferencia, q_k=1-q₁; q₂ ;q_3.... q_k-1. En el caso de dos fuentes de incertidumbre, con movimientos ascendentes (u); descendentes (d); precio de ejercicio X y valor inicial V₀, el gráfico correspondiente a un nodo de una grilla con distribución multinomial es el siguiente;

Ilustración 3: Nodo multinomial. Comportamiento del activo subyacente (Vo) y del pago contingente (Co).

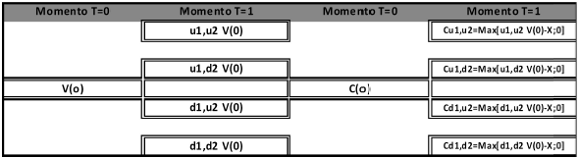
Fuente: Elaboración propia.

Previo al tratamiento específico de la técnica de valuación de opciones reales con varios riesgos, es requisito enunciar brevemente los conceptos vinculados a correlación entre eventos (fuentes de incertidumbre) y probabilidades condicionales. Estos son los insumos empleados en la estimación de los coeficientes correspondientes a los equivalentes ciertos.

3. Determinación de probabilidades neutrales al riesgo: Eventos dependientes, independientes y probabilidades condicionales

Se dice que dos eventos son independientes cuando la ocurrencia de uno no tiene ningún efecto sobre la probabilidad de ocurrencia del otro. Por el contrario dos eventos son dependientes cuando la ocurrencia de uno afecta la del otro. Cuando los eventos son dependientes se emplea el concepto de probabilidad condicional. La expresión P(X|Y) indica la probabilidad de ocurrencia del evento X dado que aconteció el evento Y.

En el caso de eventos independientes no se requieren expresiones de probabilidad condicionales. Por lo tanto la probabilidad condicional P(X|Y) siempre es igual a la probabilidad no condicional P(X). Si se conoce la probabilidad no condicional de P(Y) y la probabilidad conjunta de los eventos X e Y se puede determinar la probabilidad condicional P(X|Y) de la siguiente manera⁴;

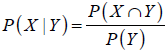Ecuación 5

3.1. Reglasde adición

La regla de la adición para eventos mutuamente excluyentes es:

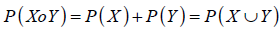Ecuación 6

En este caso es simplemente la suma de las probabilidades simples correspondientes a los eventos. Para eventos que no son mutuamente excluyentes:

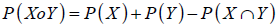Ecuación 7

A la suma de las probabilidades simples de dos eventos se le resta la probabilidad de ocurrencia conjunta de eventos (intersección).

3.2. Reglas de multiplicación

Para eventos independientes se tiene que la probabilidad de la intersección entre los eventos es simplemente el producto de las probabilidades de ocurrencia individuales;

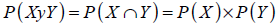Ecuación 8

Para eventos dependientes la probabilidad de ocurrencia conjunta de X e Y es igual a la probabilidad de ocurrencia de X multiplicada por la probabilidad de condicional de Y dado X. Se obtiene un valor equivalente si se invierten los dos eventos, por lo tanto la regla de la multiplicación es:

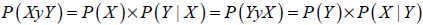Ecuación 9

Si no existe correlación entre eventos la probabilidad condicional P(X|Y) siempre es igual a la probabilidad no condicional P(X) por lo tanto la ecuación queda reducida a la expresión para eventos independientes.

3.3. Teorema de Bayes

Expresado en su forma algebraica más simple, se refiere al cálculo de la probabilidad de ocurrencia condicional del evento X dado que ha ocurrido Y. La importancia especial del teorema de Bayes consiste en que se aplica en el contexto de eventos secuenciales. Además la fórmula proporciona la base para determinar la probabilidad condicional de un evento que ha ocurrido en la primera posición secuencial, al observarse un evento específico en la segunda posición secuencial. Su expresión general es la siguiente;

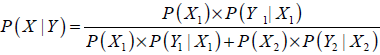Ecuación 10

El denominador de la expresión es la probabilidad global del evento en la segunda posición secuencial. En el caso de independencia entre las fuentes de incertidumbre, las probabilidades condicionales de X e Y son equivalentes a sus probabilidades no condicionales, es decir, P(Y_u| X_u)= p_uY y P(X_u| Y_u)= p_uX. En este caso se pueden encontrar las probabilidades para cada una de las cuatro posibles combinaciones, [X_u , X_d] e [Y_u , Y_d], simplemente calculando su producto (multiplicando sus respectivas probabilidades).

4. Equivalentes ciertos versus el método de carteras réplicas en la valuación de opciones reales con distribuciones multinomiales

En este caso el enfoque de carteras réplicas requiere plantear un sistema de cuatro ecuaciones con dos incógnitas. Al igual que en la distribución binomial las incógnitas son m (cantidad de activo subyacente) y B (posición en activo libre de riesgo). Queda planteado un sistema con las siguientes ecuaciones;

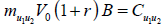	Ecuación 11
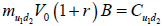	Ecuación 12
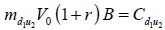	Ecuación 13
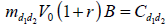	Ecuación 14

La resolución del sistema requiere de la existencia de tres activos, uno libre de riesgo y dos riesgosos correlacionados perfectamente con las fuentes de incertidumbres. En un sentido estrictamente teórico, cuando se utiliza el enfoque de grillas polinomiales y existen solamente dos activos financieros⁵, resulta complejo la aplicación del método de carteras réplicas. Operativamente se debe trabajar con un enfoque de probabilidades neutrales al riesgo, estimando los correspondientes ascensos y descensos vinculados a diferentes escenarios (Luherman, 1998b:366)

Si se emplean probabilidades neutrales al riesgo para un activo contingente (opción) con dos fuentes de incertidumbre correlacionadas o independientes, su valor es función de la suma de los valores cuatro valores correspondientes al nodo bajo examen, ponderados por el equivalente cierto asociado al estado de la naturaleza y actualizado por el tipo sin riesgo. La ecuación queda expresada de la siguiente manera;

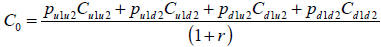Ecuación 15

Este método presenta como ventaja el hecho de resume el problema a la determinación las probabilidades neutrales al riesgo asociadas a cada estado de la naturaleza, en función de los movimientos ascendentes, descendentes y la correlación entre las fuentes de incertidumbre.

5. Opciones reales y riesgos no correlacionados. Equivalentes ciertos e incertidumbres independientes

Presentados sintéticamente los conceptos básicos correspondientes a probabilidades condicionales y dependencia de eventos, se está en condiciones de avanzar sobre la determinación del equivalente cierto para fuentes de incertidumbre no correlacionadas entre sí. En el siguiente gráfico se ilustra un nodo para el próximo periodo con eventos independientes. Suponiendo un valor inicial del activo de V₀ y fuentes de incertidumbres X e Y presentan los siguiente s valores esperados: X_t ε [X_u , X_d] con probabilidades p_ux y 1- p_ux e Y_t ε [Y_u , Y_d] con probabilidades p_uy y 1- p_uy. A su vez los movimientos multiplicativos para la primera y segunda fuente de incertidumbre se denotan como (u₁, d₁); y (u₂, d₂). La grilla está compuesta por cuatro ramas vinculadas a un nodo, donde se debe estimar el desvío estándar correspondientes a los cambios en el precio del subyacente.

Ilustración 4: Nodo grilla multinomial con eventos independientes.

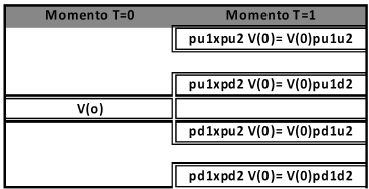
Fuente: Elaboración propia.

Las variaciones en el valor son comandadas por ambas fuentes de incertidumbre en función a las volatilidades σ₁, σ₂ y su correlación ρ_1,2. Al ser independientes las fuentes de incertidumbre las probabilidades neutrales al riesgo para cada rama surgen de aplicar las reglas de multiplicación para eventos independientes. El conjunto de ecuaciones resultantes es el siguiente;

	Ecuación 16
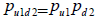	Ecuación 17
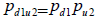	Ecuación 18
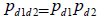	Ecuación 19

En este caso los estados de la naturaleza son independientes y excluyentes de su par. Por las reglas de multiplicación el coeficiente de probabilidad equivalente cierta es el producto de los equivalentes ciertos individuales para cada estado.

6. Opciones reales y riesgos correlacionados. Equivalentes ciertos e incertidumbres correlacionadas

Para derivar los equivalentes ciertos correspondientes a eventos dependientes es necesario introducir conceptos básicos sobre los procesos estocásticos supuestos para las fuentes de incertidumbre. Se supone que estas siguen un proceso estocástico Geométrico Browniano.

6.1. Conceptos sobre proceso estocástico Geométrico Browniano (GBM) y Aritmético Browniano (ABM)

Un movimiento Geométrico Browniano⁶ (de ahora en adelante GBM) unidimensional de parámetro σ² es un proceso estocástico {B_t:t ≥ 0} con valores en el conjunto de números reales que cumple con las siguientes propiedades:

1. Las trayectorias de la variable aleatoria t → B_t son continuas
2. El proceso tiene incrementos independientes
3. Las variables aleatorias B_t ;B_s tiene distribución normal N(0, σ² (t-s)) para cualquier intervalo de tiempo 0 ≤s < t.
4. El movimiento Browniano es un proceso de Markov. Son modelos en donde suponiendo conocido el estado presente del sistema, los estados anteriores no tienen influencia sobre los estados futuros. Se puede expresar como P(X_n+1|X_n); es decir la probabilidad del evento futuro X_n+1 solo depende del evento actual X_n y no de los eventos pasados X_n-1; X_n-2; X_n-t.
5. El movimiento Browniano es una martingala continua. Es un proceso donde el estado promedio a tiempo futuro del proceso n+1, es equivalente al valor del proceso en su último momento observado (n). Se trata de una ley de movimiento aleatoria equilibrada pues el estado no se mueve del último movimiento observado⁷.

Las condiciones que aparecen en la definición son consecuencia directa de las observaciones del fenómeno físico, pero no garantiza que tal objeto matemático exista. En 1923 el matemático Norbert Weiner demostró la existencia y unicidad de un proceso de tales condiciones. Es por ello que a menudo este proceso es conocido como proceso de Weiner: en sentido estricto el movimiento Browniano es el fenómeno físico, el modelo matemático es el proceso de Weiner, aunque es común que ambas cosas lleven el mismo nombre: movimiento Browniano.

Si el valor de un activo sigue un proceso estocástico del tipo GBM entonces el rendimiento del activo es representado por un proceso Aritmético Browniano (de ahora en adelante ABM). En el caso de GBM la distribución de probabilidad sigue un proceso lognormal. Los rendimientos al tomar valores positivos y negativos se vinculan con la distribución de probabilidad normal.

Para proyectar el comportamiento de las fuentes de incertidumbre en un enfoque multinomial el proceso estocástico empleado es el ABM. En este caso, las magnitudes de los movimientos ascendentes y descendentes cumplen con las propiedades de simetría y aditividad (Copeland y Antikarov, 2001) y adicionalmente posibilitan la combinación de los respectivos nodos. La ecuación que describe un proceso GBM es la siguiente

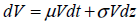Ecuación 20

Para su derivación se debe utilizar una de las principales herramientas empleadas en la teoría de opciones para resolver la ecuación diferencial parcial propuesta por el modelo de de Black-Merton-Scholes. Esta es conocida como la fórmula de Itô⁸. Sean b(t,x) y σ(t,x), una ecuación estocástica es de la forma;

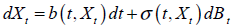Ecuación 21

Definida para valores de t en el intervalo de tiempo [0,T], para una variable aleatoria X₀ la ecuación anterior corresponde a una integral,

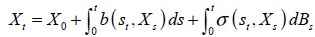Ecuación 22

En este caso el primer término representa una integral de Riemann, la segunda es una integral estocástica de Itô. El proceso X_t es conocido como proceso de Itô. (Rincón, 2008: 193). Los elementos conocidos de la ecuación son b(t,x) y σ(t,x), y la variable aleatoria inicial X_0. La incógnita del proceso es X_t. A la función b(t,x) se la conoce como coeficiente de tendencia (drift), a la función σ(t,x) se la conoce como coeficiente de difusión. El comportamiento del sistema puede interpretarse de la siguiente manera: un proceso que evoluciona de manera determinista gobernado por la parte no aleatoria de la ecuación (tendencia), pero alterado por un ruido aditivo dado por la integral estocástica (difusión). Para que una ecuación estocástica tenga solución se deben imponer condiciones de borde. Estas se presentan en los teoremas de existencia y unicidad para las ecuaciones estocásticas que establecen condiciones de regularidad para los coeficientes b(t,x) y σ(t,x), bajo el cual la ecuación tiene solución única.

Aplicada a opciones financieras y reales; la fórmula de Itô permite modelar los cambios en el valor de un activo contingente (por ejemplo una opción de compra) cuyo valor depende de otro (subyacente, activo financiero) en un periodo corto de tiempo. Si el pago contingente (C), es una función del tiempo (t) y el valor del subyacente (V), aplicando la fórmula de Itô, se tiene la siguiente expresión;

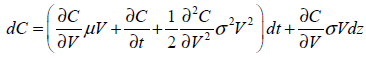Ecuación 23

Si el valor de la opción es igual a C=Ln(S), las relaciones que se plantean son las siguientes;

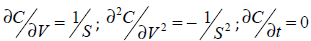Ecuación 24

Sustituyendo estas relaciones en la ecuación de Itô se obtiene explicación detalla del cambio en el valor del pago contingente como función del tendencia y el proceso de difusión,

Ecuación 25

La ecuación describe el cambio en el valor del pago contingente a partir de la tasa de crecimiento en el valor del activo subyacente. En otras palabras se procede a descomponer la expresión 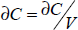, la cual representa el cambio en el flujo contingente provocado por un cambio en el valor del subyacente. De lo expuesto la tasa de crecimiento de ln (V) se encuentra normalmente distribuida con media (µ+σ²/2) y desvío estándar de σ√t.

A los efectos de ilustrar la explicación anterior supóngase que las incertidumbres del proyecto de inversión están representadas por el precio de venta (P) y cantidades demandadas (Q) de un producto en etapa de desarrollo. Con el fin de estimar el movimiento ABM y aplicar el enfoque multinomial se deben estimar pares de tasas de crecimiento y desviaciones estándares. Estas son notadas como g₁, g₂, y σ₁ σ₂ respectivamente.

En el enfoque de probabilidades neutrales al riesgo, las tasas de crecimiento correspondiente a las fuentes de incertidumbre se resumen en la magnitud presentada por la tasa de interés libre de riesgo. La derivada del cambio en el precio y la cantidad queda expresada de la siguiente manera;

Precio

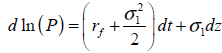	Ecuación 26
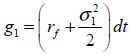	Ecuación 27

Cantidad

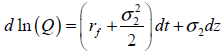	Ecuación 28
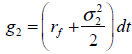	Ecuación 29

En este caso (g₁, g₂) siguen un proceso estocástico ABM con ascensos y descensos constantes de signos opuestos (u=-d). Las combinaciones de los posibles valores que pueden asumir las variables se detallan a continuación;

Ilustración 5: Nodo multinomial y fuentes de incertidumbre correlacionadas (Po) precio; (Qo) cantidades.

Fuente: Elaboración propia.

6.2. Determinación de los coeficientes de equivalencia a certidumbre

Para determinar los coeficientes correspondientes a probabilidades neutrales al riesgo previamente es necesario calcular los siguientes insumos de cada fuente de incertidumbre;

1. Tasa de crecimiento g;
2. Volatilidad σ
3. Correlación ρ,

Suponiendo que las variables aleatorias siguen un proceso ABM se aplican las reglas de multiplicación, el Teorema de Bayes para probabilidades condicionales; se plantea un sistema de seis ecuaciones con seis incógnitas agrupadas de la siguiente manera:

El primer grupo determina la tasa esperada de crecimiento para las fuentes de incertidumbre;

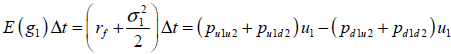	Ecuación 30
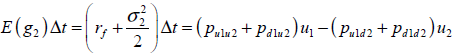	Ecuación 31

El segundo grupo modela la volatilidad del crecimiento para ambas variables aleatorias;

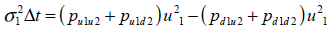	Ecuación 32
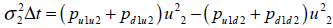	Ecuación 33

Ecuación que refleja el término de correlación (si las fuentes son independientes supone un valor cero)

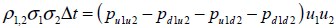Ecuación 34

Ecuación de control, requerimiento para que la suma de probabilidades sea igual a 1;

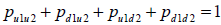Ecuación 35

Resolviendo el sistema de seis ecuaciones planteado se obtienen las probabilidades neutrales al riesgo correspondiente a cada estado;

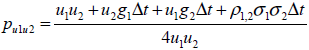	Ecuación 36
	Ecuación 37
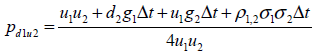	Ecuación 38
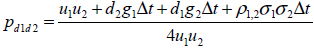	Ecuación 39

Las otras dos incógnitas que resultan del sistema son los movimientos ascendentes y descendentes;

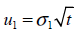	Ecuación 40
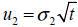	Ecuación 41

7. Un caso de aplicación. La opción de abandono y el enfoque multinonial

Con el fin de ilustrar el desarrollo precedente se adapta el ejemplo desarrollado por Copeland y Antikarov (2001) sobre el tratamiento de una opción de abandono incorporada a un proyecto de desarrollo de producto. Para ello supóngase un proyecto de inversión que consista en el desarrollo de un producto donde se presentan dos fuentes de incertidumbre: el precio (P) a ser comercializado y las cantidades (Q) demandadas. El periodo de tiempo que dura el desarrollo es de seis meses y la corriente de flujo de fondos es igual a PxQ menos los costos fijos (CF) de $4.000. Al final del segundo periodo los flujos de fondos se transforman en una perpetuidad constante equivalente a múltiplo de seis. El proyecto puede ser vendido a un competidor (abandono) en cualquier momento de su fase de desarrollo por un valor de $50.000. La tasa continua anual libre de riesgo es de 5%.

El procedimiento consta de 5 pasos los cuales se desarrollan a continuación:

Paso 1: Identificación de las variables relevantes: En el cuadro 1 y 2 se exponen los datos del problema y las variables correspondientes a los supuestos sobre el comportamiento de cada fuente de incertidumbre; precio y cantidad demandada.

Cuadro 1: Parámetros correspondientes del proyecto R&D.

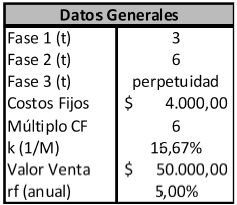
Fuente: Elaboración propia.

Cuadro 2: Parámetros correspondientes a las fuentes de incertidumbre (Q) cantidades y (P) precios.

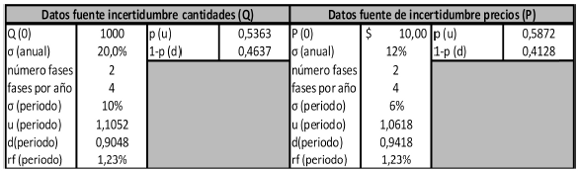
Fuente: Elaboración propia.

En el ejemplo, la volatilidad para el precio y las cantidades son un dato dado⁹ expresados en términos anuales. A partir de allí se estima la volatilidad periódica aplicando la siguiente ecuación¹⁰;

Ecuación 42

Paso 2: determinación de los movimientos de ascenso y descenso correspondiente a las variables aleatorias: Se supone que los movimientos de ascenso (u) y descenso (d) siguen un proceso estocástico GBM, con distribución de probabilidad lognormal empleando la transformación para la estimación de los parámetros (Cox, Ross y Rubinstein, 1979);

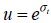	Ecuación 43
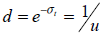	Ecuación 44

Para las fuentes de incertidumbre las probabilidades neutrales al riesgo p y 1-p se estiman con los u y d correspondientes a cada una;

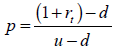Ecuación 45

El comportamiento de la variable aleatoria Q (cantidades demandadas) se ilustra

Ilustración 6: Procesos estocástico y tasas de crecimiento correspondiente a cantidades demandadas del producto en desarrollo.

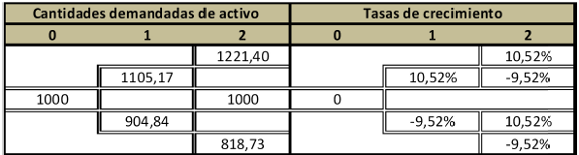
Fuente: Elaboración propia.

El gráfico 6 presenta los valores probables, para un horizonte temporal de dos periodos, correspondientes a las cantidades demandas del producto. Para ello se aplicaron los respectivos coeficientes de ascenso y descenso .

Las tasas de crecimiento para los diferentes estados surgen de los cocientes; primer periodo:

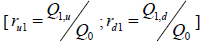primer periodo:segundo periodo: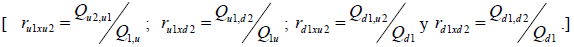

Ilustración 7: Procesos estocástico y tasas de crecimiento correspondiente a precios del producto en desarrollo.

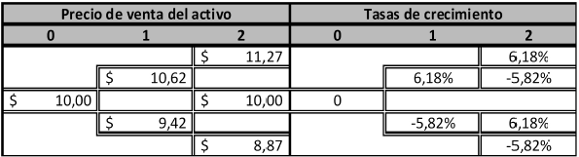
Fuente: Elaboración propia.

De igual manera se estimo el recorrido de la variable aleatoria P (precio del producto) en donde se expone el recorrido proyectado para los dos periodos de tiempo; (P_i,jxd ; P_i,jxu) y las tasas de crecimiento primer periodo: 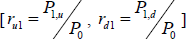; segundo periodo: 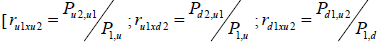y .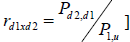

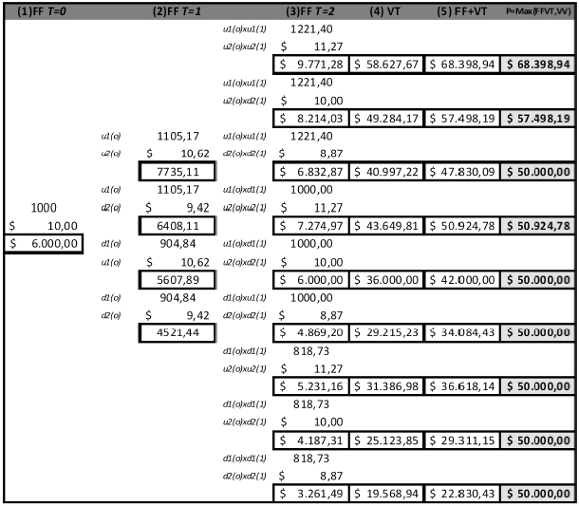
Paso 3: Construcción de la grilla, los flujos de fondos asociados a cada estado y el valor contingente al vencimiento: A continuación se presenta la grilla correspondiente a las fuentes de incertidumbre precio y cantidades. Es el paso previo y necesario a la determinación del flujo de caja para cada estado de la naturaleza. Conforme se anticipo los flujos de fondos son el resultado de la suma algebraica [FF = P x Q-CF] para los diferentes casilleros de la grilla. En la ilustración 8, columnas 1, 2 y 3 se desarrollan los flujos de fondos correspondientes a cada periodo. Formalmente se los plantea como;

Ilustración 8: Grilla combinada para fuentes de incertidumbre (Precios, Cantidades, Flujos de Fondos y Opción en T=2).

Fuente: Elaboración propia.

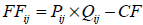Ecuación 46

En la columna 4 se expone el cálculo del valor terminal, suponiendo como representativa de la medida indicada el resultado del producto entre un múltiplo (M) equivalente a seis veces el flujo y el flujo del último periodo para cada estado,

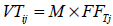Ecuación 47

La columna 5 representa el valor del proyecto finalizado su desarrollo. Este surge de adicionar el flujo en el periodo dos al valor terminal estimado. Finalmente, en la columna 6 se expone el valor que asume el pago contingente al vencimiento. Este es el máximo valor entre continuar o abandonar, en este caso vendiendo el desarrollo por la suma de $50.000 (valor de venta (VV));

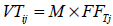Ecuación 48

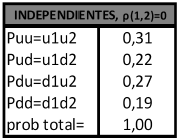
Paso 4.1: Determinación de los coeficientes de probabilidades neutrales al riesgo para incertidumbres independientes: Suponiendo inexistencia de correlación entre las fuentes de incertidumbre precio y cantidad; se aplican las reglas de multiplicación para eventos independiente y probabilidades no condicionales con el objetivo de calcular las probabilidades neutrales al riesgo. Estas son expuestas en el siguiente cuadro.

Cuadro 3: Coeficientes de probabilidades neutrales al riesgo con ρ (1,2)=0.

Fuente: Elaboración propia.

A título de ejemplo se desarrolla el cálculo de las probabilidades combinadas correspondiente a los nodos ascendentes u1, u2. Para ello se toman los coeficientes de probabilidades neutrales al riesgo individuales de cada incertidumbre (paso 2) y se los multiplica; en este caso se tiene: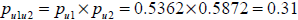

Con los coeficientes de probabilidades neutrales al riesgo se está en condiciones de calcular los valores equivalentes ciertos y actualizarlos al tipo sin riesgo, método a explicar en el quinto y último paso. A continuación se expone la grilla con los respectivos valores;

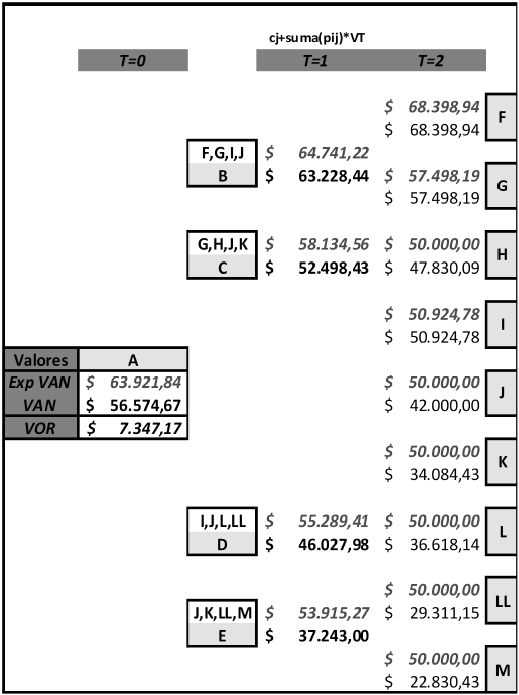
Paso 5.1: Determinación del valor de la opción para eventos independientes: En este caso se calcula el valor sin opciones (VAN), el valor con opciones o valor expandido (ExpVAN) y por diferencia el valor de las opciones (VOR) (Trigeorgis, 1995; Mun, 2004) conforme surge de la ilustración 9. En el gráfico se individualiza a cada estado con una letra. Se emplea el procedimiento de resolución recursiva (del atrás hacia al principio) y por estado se expone el valor con opción y sin opción. Para estimar el valor en los nodos del primer periodo se emplea el método de equivalente cierto conforme se expone en la siguiente ecuación;

Ilustración 9: Valoración de la inversión sin opciones e incorporando la flexibilidad estratégica para fuentes de incertidumbre independientes.

Fuente: Elaboración propia.

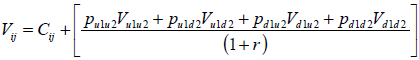Ecuación 49

Tomando como ejemplo el nodo B; previo se debe sumar el flujo de fondos en el periodo 1 para dicho nodo y el valor actual con opción y sin opción correspondiente a los estados F, G, I, J. La ecuación queda planteada de la siguiente manera;

Nodo B con opciones: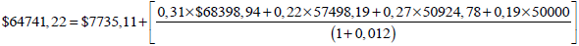

Nodo B sin opciones: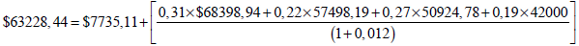

De la idéntica manera se resuelven los restantes nodos hasta llegar al valor en el nodo A (principio temporal de la grilla). La diferencia entre el valor expandido (ExpVAN) y el valor sin opciones (VAN) es igual al valor adicional generado por la flexibilidad estratégica de poder vender (abandonar) el proyecto en manos de un competidor (VOR), o sea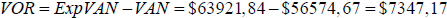

Paso 4.2: Determinación de los coeficientes de probabilidades neutrales al riesgo para incertidumbres correlacionadas: En el siguiente cuadro se explicitan las variables que oficiaran de insumos;

Cuadro 4: Variables y coeficientes de probabilidades neutrales al riesgo para con ρ (1,2)=-0,4

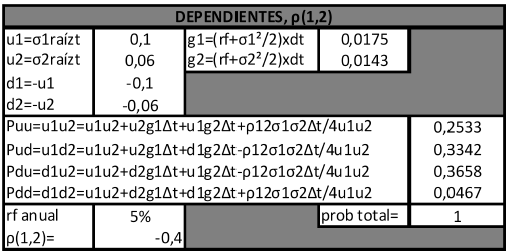
Fuente: Elaboración propia.

Ilustración 10: Valoración de la inversión sin opciones e incorporando la flexibilidad estratégica para fuentes de incertidumbre correlacionadas.

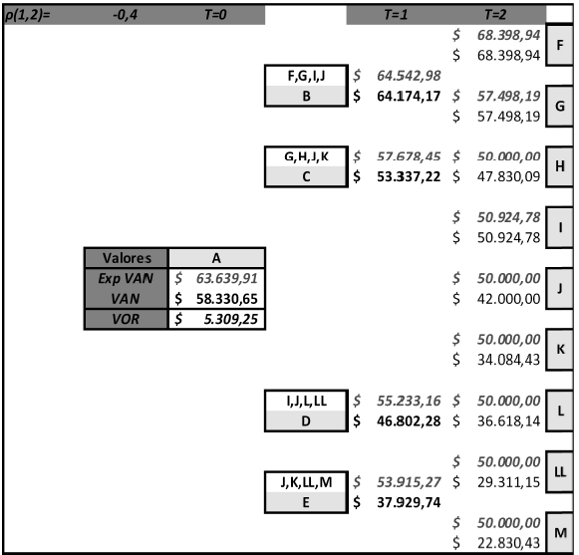
Fuente: Elaboración propia.

Para este caso se supone una correlación de -0,4 entre las variables aleatorias precio y cantidades demanda del producto en desarrollo. Nuevamente la clave del proceso de valuación reside en la estimación de las probabilidades neutrales al riesgo. Suponiendo que las fuentes de incertidumbre siguen un proceso ABM se deben estimar los siguientes parámetros;

Cantidades: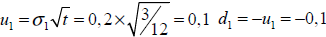

Precios: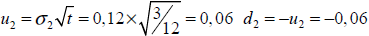

Cantidades tasa de crecimiento: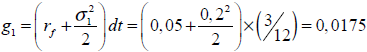

Precio tasa de crecimiento: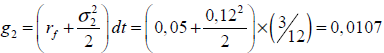

El valor correspondiente al conjunto de coeficientes de probabilidades neutrales al riesgo se obtiene aplicando el siguiente grupo de ecuaciones

Paso 5.2: Determinación del valor de la opción eventos dependientes: Finalmente el procedimiento de resolución es equivalente al de variables aleatorias independientes (paso 5.1). El desarrollo gráfico del proceso recursivo se expone en la ilustración 10. A título de ejemplo se explicita el cálculo del nodo B;

Nodo B con opciones: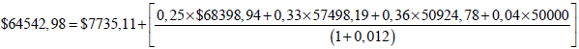

Nodo B sin opciones: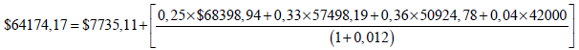

Al igual que en el caso de independencia se resuelven los restantes nodos hasta llegar al valor en el nodo A. La diferencia entre el valor expandido (ExpVAN) y el valor sin opciones (VAN) es el valor adicional generado por la flexibilidad estratégica de poder vender (abandonar) el proyecto en manos de un competidor, en este caso con correlación;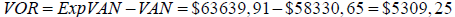

8. Conclusiones

Es común que los problemas de inversión tratados bajo el enfoque de opciones reales reduzcan la complejidad del proceso estocástico a una fuente de incertidumbre. La resolución en tiempo discreto se limita a modelar el proceso estocástico con la distribución de probabilidad binomial y al empleo de carteras réplicas o probabilidades neutrales al riesgo para la valuación de la flexibilidad estratégica contenida en la decisión de inversión.

La pluralidad de incertidumbres torna indispensable trabajar con un enfoque general como el de la distribución de probabilidad multinomiales. Esta constituye el marco general para el caso particular de la distribución binomial.

Aplicando los principios básicos sobre probabilidades condicionales y el movimiento Browniano se derivan los coeficientes que reflejan las probabilidades neutrales al riesgo para la grilla multinomial. Paralelamente se fundamentó la conveniencia de trabajar con grillas binomiales o multinomiales.

En síntesis, para lograr la implementación del método en un entorno amigable y operativo se requiere transitar cinco etapas:

1. Identificación de las variables relevantes del problema y flexibilidad estratégica de la inversión.
2. Definir el proceso estocástico correspondiente a las variables aleatorias: asumir un proceso estocástico con movimiento Browniano derivando movimientos, tendencias y difusión
3. Estimar independencia o correlación de las variables aleatorias. Paralelamente empleo de grilla multinomiales para el diagrama del recorrido aleatorio correspondiente a la combinación de fuentes de incertidumbre.
4. Determinación de los coeficientes de probabilidades neutrales al riesgo de eventos dependientes e independientes. Empleo del método de equivalentes ciertos.
5. Calcular recursivamente el valor actual neto tradicional (VAN), el valor con opciones (ExpVAN) y por diferencia el valor de las opciones reales (VOR).

Notas
¹ Se pueden diferenciar cuatro grupos de métodos de valuación de activos reales: (a)Valores Históricos (basados en el criterio de costos y en donde se engloban los métodos contables); (b) Múltiplos y Comparables (los ratios más difundidos: Precio-Ganancia (PER); Valor de Mercado-Valor de Libros, Enterprise Value; Q-Tobin y demás múltiplos de acuerdo a las características de la inversión); (c) Valores Intrínsecos (Descuento de Flujos de Fondos en sus diferentes variantes; Ganancias Residuales y Valor Económico Añadido); (d) Enfoque de Opciones Reales; (Milanesi, 2009).
² Cabe tener en cuenta que para la resolución del problema, en este caso se asume que resulta indistinto al decidor, el modo en que se arriba a un cierto estado final y esto puede no ser un supuesto aceptable en la práctica. De cualquier modo, si ese fuera el caso, se podría considerar cada camino como un estado independiente con su correspondiente probabilidad y a partir de esta definición, llegar a la solución con el mismo procedimiento. Esta situación refleja la gran flexibilidad de las rejillas para adaptar la formulación del problema a distintos contextos.
³ El Triángulo de Pascal o Tartaglia. Se tienen referencias que datan del siglo XII en China. De hecho, algunas de sus propiedades ya fueron estudiadas por el matemático chino Yang Hui (siglo XIII), así como el poeta persa Omar Khayyam (siglo XII). Asociar el nombre del triángulo al filósofo y matemático Blas (Blaisé) Pascal (1623-1662) se debe a que el francés escribió el primer tratado sobre el triángulo. El matemático italiano Niccolo Fontana Tartaglia (1500-1557) fue uno de los primeros que publicó y difundió en Europa de la Edad Moderna la herramienta matemática en cuestión.
⁴ Por lo general se confunden los conceptos de eventos mutuamente excluyentes y no excluyentes con dependencia e independencia. La condición de mutua exclusividad implica que dos eventos no pueden acontecer simultáneamente, en tanto que la independencia indica que la ocurrencia de un evento no es afectada por otro.
⁵ En el caso de que existan dos activos si se pretende construir carteras réplicas para valuar el riesgo de precio y el riesgo de cantidades producidas, por ejemplo una explotación agropecuaria, puede tomarse el precio spot para replicar riesgo precio más no existe activo financiero réplica o "gemelo" para construir una cartera de cobertura contra el riesgo de cantidades.
⁶ El movimiento Browniano tiene reconoce sus orígenes cuando en el año 1828 el botánico Robert Brown reportó en una revista científica que los granos de pole suspendidos en una cierta sustancia y vistos a través de un microscopio realizaban un movimiento irregular e inexplicable. Luego de años de experimentación y debate este movimiento es entendido y explicado a través de las múltiples colisiones aleatorias de las moléculas del líquido con los granos de polen. Llegar a tal aseveración tomo años pues debió aceptarse la teoría cinético molecular de la materia, y el seminal trabajo de Albert Einsten de 1905 sobre este fenómeno contribuyo decididamente a tal tarea (Rincón, 2008: 191).
⁷ A estos procesos se los conoce como de juegos justos pues si se considera una serie infinita de apuestas sucesivas y si el capital de un jugador se denota como X_n, al tiempo n, la propiedad de martingala establece que el juego es justo ya que en promedio el jugador no pierde ni gana en cada apuesta.
⁸ El nombre del proceso es en honor a su padre el matemático Kiyosi Itô, publicado en el artículo "On stochastics processes (infinitely divisible laws of probability) Japanese Journal of Mathematics (Fornero, 2008)
⁹ Por lo general se trabaja observando series de datos correspondientes a las variables aleatorias o en su defecto simulando el comportamiento de las misma y como producto de la simulación emplear los parámetros media y desvío de cada variable.
¹⁰ La ecuación 42 es correcta en la medida que la volatilidades mensuales puedan considerarse variables aleatorias independientes.

Referencias bibliográficas
1. Black, F. y Scholes, M. (1973). "The Pricing of Options and Corporate Liabilities", Journal of Political Economics, n° 81, pp. 637-654.
2. Boyle, P. Evine, J. y Gibbs, S. (1989). "Numerical evaluating of multivariate contingent claims", Review of Financial Studies, n° 2, pp. 241-252.
3. Brandao, L. y Dyer, J. (2009). "Projectos de opcoes reais com incertezas correlacionadas", BASE-Revista de Administração e Contabilidade de Unsinos, enero/abril, pp. 19-28.
4. Brennan, M. y Schwartz, E. (1985). "Evaluating Natural Resources Investment", Journal of Business, n° 58, pp. 135-157.
5. Brennan, M. y Schwartz, E. (1985). "A New Approach to Evaluating Natural Resources Investment", Midland Corporate Financial Journal, n° 3, pp. 37-47.
6. Copeland, T. y Antikarov, V. (2001). Real Options. Texere LLC, New York.
7. Copeland, T. y Tufano, P. (2004). "A real World to Manage Real Options", Harvard Business Review, n° 82, pp. 90-99.
8. Cox, J. y Ross, S. (1976). "The Valuation of Options for Alternative Stochastics Process", Journal of Financial Economics 7, n° 3, pp. 145-166.
9. Cox, J. Ross, S. y Rubinstein, M. (1979). "Option Pricing: A Simplified Approach", Journal of Financial Economics, n° 3, pp. 229-263.
10. Dixit, A. y Pindyck, R. (1994). Investment Under Uncertainty. Princeton University Press, New Jersey.
11. Fornero, R. (2008). Cronología de las Finanzas. Fondo Editorial del Consejo Profesional de la Ciudad Autónoma de Buenos Aires, Buenos Aires.
12. Hull, J. (2005). Options, Futures and Others Derivatives. Prentice Hall, New Jersey.
13. Ingersoll, J. y Ross, S. (1992). "Waiting to Invest: Investment and Uncertainty", Journal of Business, n° 65, pp. 1-29.
14. Kemma, Angelien. "Options in Real and Financial Markets". WP. Ph.D dissertation, Erasmus University (1988).
15. Kulatilaka, N. (1988). "Valuing the Flexibility of Flexible Manufacturing Systems", IEEE Transactions on Engineering Management, n° 22, pp. 250-257.
16. Kulatilaka, N. (1995). Operating Flexibilities in Capital Budgeting: Substitutability and Complementary in Real Options. Real Options in Capital Investment: Models, Strategies and Applications, Praeger, Westport Connecticut.
17. Luherman, T. (1998). "Investment opportunities as real options: Get starting with the numbers", Harvard Business Review, n° 4, pp. 51-67.
18. Luherman, T. (1998). Investment Science. Oxford University Press, New York.
19. Margrabe, W. (1978). "The Value of an Option to Exchange one Asset for Another", Journal of Finance, n° 33, pp. 177-186.
20. Mason, S. y Merton R. (1985). "The Role of Contingent Claims Analysis in Corporate Finance" en E. Altman y M. Subrahmanyam (ed.) Recent Advances in Corporate Finance, Richard Irwin.
21. Mc Donal, R. y Siegel, J. (1986). "Investment and the Valuation of Firms When There is an Option to Shut Down", International Economic Review, n° 26, pp. 321-349.
22. Merton, R. (1973). "The Theory of Rational Option Pricing", Bell Journal of Economics and Management Science, pp. 141-183.
23. Milanesi, G. (2009). Administración Financiera: Teoría y Valuación. Induvio, Buenos Aires, 1° edición.
24. Milanesi, G. y Vigier, H. (2010). Árboles de decisiones, opciones reales y enfoque integrado en mercados completos e incompletos. XLV Reunión Anual de la Asociación Argentina de Economía Política, AAEP, 15 y 19 de Noviembre Universidad Nacional de Buenos Aires, disponible en http://www.aaep.org.ar/anales/buscador.php?anales=2010-CABA, ISSN 1852-0022, ISBN 978-987-99570-8-0.
25. Mood, A. y Graybill, F. (1978). Introducción a la Teoría de la Estadística. Aguilar, Madrid, 2° edición.
26. Mun, J. (2004). Real Options Analysis: Tools and Techniques for Valuing Strategic Investment and Decisions. Wiley, New York.
27. Myers, S. (1977). "Determinants of Corporate Borrowing", Journal of Financial Economics 5, n° 2, pp. 147-176.
28. Myers, S. y Majd S. (1990). "Abandonment Value and Project Life", Advances in Futures and Options Research, pp. 1-21.
29. Paddock, J., Siegel, D. y Smith, J. (1988). "Option Valuation of Claims on Physical Assets: The Case of Offshore Petroleum Lease", Quarterly Journal of Economics, n° 103, pp. 479-508.
30. Pindyck, R. (1988). "Irreversible Investment, Capacity Choice, and the Value of the Firm", American Economics Review, n° 78, pp. 969-985.
31. Rincón, L. (2008). Introducción a los Procesos Estocásticos. Papeles de Trabajo Departamento de Matemáticas, Facultad de Ciencias (UNAM) Circuito Exterior.
32. Smit, H. (1996). "The Valuating of Offshore Concessions in the Netherlands", Financial Management, n° 26, pp. 5-17.
33. Smith, J. y Nau, R. (1995). "Valuing Risky Projects: Options Pricing Theory and Decision Analysis", Management Science, n° 41, pp. 795-896.
34. Trigeorgis, L. (1988). "A Conceptual Options Framework for Capital Budgeting", Advances in Futures and Options Research, pp. 145-167.
35. Trigeorgis, L. (1993). "Real Options and Interactions with Financial Flexibility", Financial Management, n° 22, pp. 202-224.
36. Trigeorgis, L. (1995). Real options in capital investments: models, strategies and applications. Praeger, London.
37. Trigeorgis, L. (1997). Real options: managerial flexibility and strategy in resource allocation. MIT Press, Cambridge, 2° edición.
38. Trigeorgis, L. y Mason, S. (1987) "Valuing Managerial Flexibility", Midland Corporate Finance, n° 5, pp. 14-21.
39. Trigeorgis, L. y Smit, H. (2006) Real Options and Game Theory. Preager, Princenton Universirty Press; Princenton and Oxford.