Valor de proyectos de inversión con estimaciones probabilísticas y borrosas^•

Project valuation with probabilistic and fuzzy estimates

Ricardo A. Fornero^♦

^♦ Universidad Nacional de Cuyo, e-mail: rfornero@fcemail.uncu.edu.ar.

Resumen
La valuación de un proyecto de inversión o de un negocio generalmente se realiza considerando una tasa de actualización ajustada por riesgo que compensa la incertidumbre a la que está expuesto el flujo de fondos. Se suelen usar técnicas con base probabilística o borrosa para reflejar la propagación de la incertidumbre de las variables básicas del negocio con las que se realiza la estimación del flujo de fondos; y también se suele distinguir entre la incertidumbre como variabilidad aleatoria y la imprecisión (o incertidumbre epistémica). En este ensayo se explican las variantes metodológicas para obtener una estimación puntual del valor, o bien una estimación en un intervalo. Se hace especial referencia a las situaciones en que puede determinarse un valor probabilístico o un valor borroso, de un modo que sea congruente con una valuación que emplea una tasa ajustada por riesgo.

Palabras clave: Valuación; Simulación de Montecarlo; Números borrosos.

Abstract
Valuation of an investment project or a business is usually done considering a risk adjusted discount rate, which compensates for the uncertainty that affects the estimated cash flow. Commonly, probabilistic or fuzzy techniques are used to reflect the uncertainty propagation of the business' primary variables with which the cash-flow is estimated. Also, usually a distinction between aleatory uncertainty (or random variability) and imprecision (or epistemic uncertainty) is made. This paper explains the methodological variants to obtain a point value estimate, or an interval value estimate. Particular attention is made to the situations in which probabilistic value or fuzzy value can be determined, in a way consistent with a valuation that uses a risk-adjusted discount rate.

Key words: Valuation; Monte Carlo simulation; Fuzzy numbers.

JEL: G31

1. Introducción

Existen alternativas metodológicas para determinar el valor de un proyecto de inversión (o, genéricamente, de un negocio) considerando la incertidumbre a la que están expuestos los resultados. La forma más difundida en términos prácticos implica el uso de una tasa de actualización ajustada por riesgo, según el grado de riesgo del flujo de fondos que surge del análisis del negocio.

Esa identificación del riesgo puede realizarse de modo cualitativo o por sensibilidad, o bien con alguna medición del impacto de la incertidumbre en el flujo de fondos. La técnica usual para esta medición es de base probabilística (mediante simulación probabilística, o con el análisis cuantitativo de escenarios).

Debido a que una parte de la incertidumbre se origina en el carácter parcial o incompleto de la información que se emplea, también se considera que esa imprecisión puede reflejarse mediante la estimación de las magnitudes como números borrosos (fuzzy numbers). Si bien en esas propuestas se enfatiza que la expresión borrosa puede ser la más adecuada para reflejar la imprecisión de las estimaciones, hay que considerar que existen nociones de índole probabilística que hacen posible un reconocimiento similar.

Ambas formas de medición (probabilística y borrosa) son herramientas para reflejar la propagación de la incertidumbre de las variables básicas (económicas o técnicas) que se consideran, hasta llegar al flujo de fondos del negocio. En la valuación, el flujo de fondos así analizado debe tratarse de un modo que sea congruente con la tasa de actualización que se emplea.

No ocurre esto último en muchas de las propuestas que trabajan con medidas probabilísticas o borrosas. Se ha difundido una modalidad de análisis de riesgo de un proyecto de inversión que se basa en la determinación de un "valor probabilístico" o un "valor borroso", realizado a partir del flujo de fondos y de una tasa de actualización ajustada por riesgo.

El análisis de riesgo, en realidad, puede hacerse con respecto al flujo de fondos y sus componentes, y sobre esa base se realiza la valuación. El planteo de una distribución completa (de probabilidad o de posibilidad) de la estimación de valor es conceptualmente incorrecto y (tal vez por eso mismo) produce confusiones prácticas.

En este ensayo se comentan las similitudes y las diferencias de la valuación con estimaciones probabilísticas y borrosas del flujo de fondos. Específicamente, se consideran las formas de operar que son congruentes con el sentido de la valuación y las precauciones que deben tenerse al usar la noción de un "valor probabilístico".

En el punto 2 se sintetizan los principales aspectos de la valuación con el flujo de fondos, y en el punto 3 se resumen las formas probabilística y borrosa de estimación del flujo de fondos. Esto se vincula con el efecto que se considera de las nociones de variabilidad e imprecisión, y con la tasa ajustada por riesgo. Los temas se esquematizan en la figura 1.

Figura 1 Valuación: Flujo de fondos y tasa ajustada por riesgo

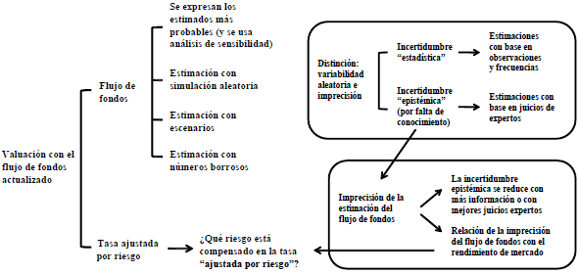
El modo de operar para la valuación en ambos casos se presenta en los puntos 4 y 5. Primero se plantea la valuación como una estimación puntual de valor, y después se considera la expresión de un intervalo o rango de valor. Esto requiere comentar las características de la estimación, en términos de la imprecisión y de la relación con la compensación por riesgo que se incluye en la tasa de actualización. De esta forma se caracteriza el que puede considerarse un auténtico valor borroso. En la figura 2 se muestra un esquema del análisis que se presenta.

Figura 2 Valor: Estimación puntual y en un rango, con mediciones probabilísticas y borrosas

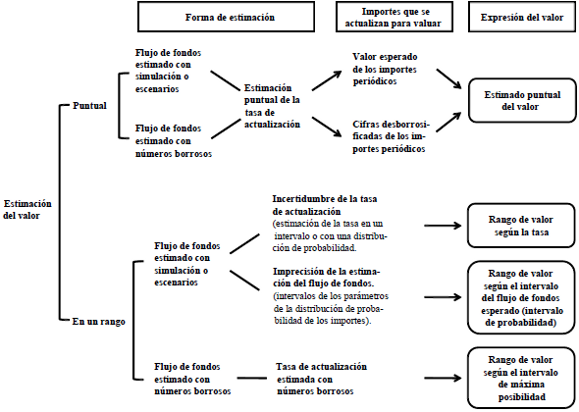
En los puntos 6 y 7 se comentan otros aspectos relacionados con el valor estimado con una u otra base. El punto 6 muestra el encuadre conceptual que tiene la estimación de un valor en un momento futuro, que es el caso de las estimaciones que se usan en las técnicas de valuación que incluyen el reconocimiento explícito de la flexibilidad (como un árbol de decisiones, o el valor de opciones reales contenidas en un proyecto o negocio).

Y en el punto 7 se señalan los principales problemas que tiene la noción de un "valor probabilístico" y de su equivalente posibilístico (que es un valor que se denomina borroso, aunque podría decirse que es un valor incorrectamente denominado borroso).

Como se expresa, el punto de referencia en este ensayo es la valuación (monetaria) de un proyecto o un negocio, y no sólo la determinación de una medida que permita la comparación entre alternativas (que se denomina selección de proyectos en el proceso de evaluación).

La situación de valuación requiere una estimación razonable y se considera que el grado de detalle del análisis es el suficiente para esa razonabilidad. Es decir, la medición no consiste, en un extremo, en una cuenta preliminar con estimaciones muy genéricas; ni supone, en el otro extremo, un análisis de riesgo muy específico y pormenorizado.

Por la variedad de nociones y de herramientas que intervienen, y para no afectar demasiado la línea de desarrollo, algunos aspectos se detallan en apéndices. Por la misma razón, y porque no parecen esenciales para la presente argumentación, no se incluyen los aspectos conductuales de la decisión de inversión, y tampoco el tratamiento explícito de la flexibilidad que puede estar contenida en el proyecto de negocio (más allá del comentario relacionado con este tema en el punto 6).

2. Valuación con el flujo de fondos

El valor de un proyecto de inversión (y, genéricamente, el valor de un negocio) es la cifra en que se puede realizar la transacción de un flujo de fondos como el que se estima para el proyecto. También puede entenderse como una medida del efecto que tiene el proyecto en el valor de la empresa que considera esa inversión.

La medición, en principio, se refiere a un valor transable, un precio: es el valor de un título (o una cartera de títulos) con un perfil temporal y grado de riesgo del flujo de fondos similar al del proyecto o negocio. Entonces, con el flujo de fondos que se estima para el proyecto se considera la cartera de títulos que es equivalente, y la suma de sus precios es el valor del proyecto.

Este valor es independiente de la preferencia temporal por consumo del decididor (o inversor), ya que él puede ajustar el flujo de efectivo que requiere para su perfil de consumo mediante transacciones con títulos. Las condiciones de esto se conocen como el enunciado de separación de Fisher-Hirshleifer (que se resume en el apéndice 1)¹.

Si no existen títulos transados que sean directamente equivalentes al proyecto o el negocio, el valor se mide como una estimación del precio que tendría un título con ese flujo de fondos, si se transara (es decir, el precio de mercado del derecho a obtener ese flujo de fondos). Esta valuación se realiza como el valor actual del flujo de fondos estimado para el proyecto, considerando una tasa de actualización que es congruente con esa medición de los importes periódicos.

Con el perfil estimado del flujo de fondos, 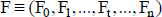, y una tasa de actualización r, el valor se calcula:

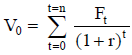Ecuación 1

Según sea el perfil del flujo de fondos estimado (con la división de períodos que se use en cada caso) puede existir un importe en el momento al que se refiere la valuación 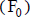. Al considerar este importe en el cálculo, el valor que se obtiene es una medida neta, antes de realizar algún compromiso de fondos en el proyecto².

La forma más difundida es la valuación con una tasa ajustada por el riesgo del flujo de fondos. Esa tasa se estima como una aproximación razonable a la tasa de rendimiento requerido en el mercado de capital para un flujo de fondos con características similares al que se estima. Sin entrar en detalles que no hacen a la finalidad de este ensayo, consideremos que la tasa puede medirse con alguna forma aplicable del modelo de valoración de títulos (CAPM, capital asset pricing model)³.

Alternativamente, el valor de un proyecto se puede determinar con la perspectiva del decididor, considerando el rendimiento que requiere para comprometer el capital, capital que se recuperará al obtenerse el flujo de fondos del proyecto según la estimación realizada.

En cualquiera de estos casos, para la valuación es necesario estimar el flujo de fondos del proyecto y evaluar el riesgo, es decir, la incertidumbre a la que están expuestos los resultados de la inversión.

Tal estimación suele reflejar la opinión de expertos o analistas, opinión que se refiere tanto al negocio y su desempeño como a los títulos que son comparables (o el rendimiento que sería comparable en el mercado de capital). Quien decide acerca del proyecto pone en relación la estimación de valor así realizada con la situación individual u organizacional que considera pertinente⁴. Podría decirse que de este modo quedarían separadas la descripción de desempeño y riesgo (y el valor calculado) de las consideraciones personales o políticas en la organización, según las cuales esa valuación se evalúa en términos de la conveniencia de una decisión.

Existen variantes metodológicas para expresar la estimación del flujo de fondos de un proyecto o negocio, y para operar con ellas y obtener el valor. A continuación se considera el modo en que esas variantes permiten obtener una estimación de valor que sea coherente con las nociones aquí resumidas.

3. Flujo de fondos: Estimaciones probabilísticas y borrosas

3.1 Modelo financiero del proyecto y una primera forma de estimar el valor

La estimación del flujo de fondos de un proyecto o de un negocio se realiza con un modelo en el que se representa la situación económica y técnica pertinente: inversión, cantidades, precios, costos, impuestos. Estas son las variables con las que se determinan las magnitudes de los componentes del flujo de fondos: ganancia, impuestos, y activos y pasivos operativos.

Cada una de esas variables es el resultado de una estimación explícita (o de una consideración implícita) de variables primarias y de relaciones entre ellas. Por ejemplo, la estimación de ventas y costos puede hacerse a partir de la estimación del crecimiento de la economía, de la estructura interna del sector (evolución, competidores, esfuerzo comercial, etc.), de los procesos y tecnología que se consideran, de la evolución de los sectores relacionados, y de la expectativa de precios internos e internacionales.

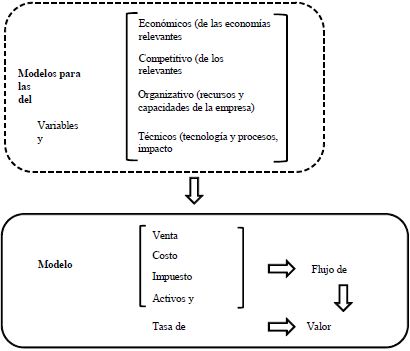
Estas variables y relaciones se consideran con modelos económicos, organizativos, técnicos (o ingenieriles), y de otra índole, y el grado de detalle depende de la finalidad de la evaluación y de la disponibilidad de información para los analistas.

El conjunto puede verse como una descripción del negocio abierta en diferentes niveles de modelos (figura 3). En cada nivel se identifican los factores de incertidumbre a los que está expuesto el negocio. El último nivel es el modelo financiero (los componentes del flujo de fondos), y a partir de éste se realiza la valuación.

Figura 3 Niveles de estimación

Más allá del grado de detalle de la estimación (las variables primarias que se consideran), la forma más simple (y bastante difundida) es trabajar sólo con los importes periódicos más probables del flujo de fondos, 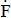. Estos se obtienen con la magnitud, también más probable, de las variables que se consideran para formar el modelo del flujo de fondos.

Según las características de riesgo que se evalúan implícitamente en esta medición (o con alguna aproximación de sensibilidad), se estima una tasa de actualización congruente; digamos, una tasa de actualización k que contiene una compensación por el riesgo de la inversión. Consideremos que esa tasa es única para todo el horizonte, y que se realiza una estimación puntual, 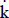. En ese caso, el valor del proyecto se calcula:

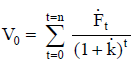Ecuación 2

La tasa de actualización compensa el riesgo del flujo de fondos, y por eso el valor 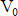es una estimación puntual del precio de ese flujo de fondos en el momento de la valuación.

Más adelante (en el punto 5) se comenta que la estimación puede explicitar un rango para el valor, si se plantea un factor de error en la estimación (por ejemplo, +/- 3%) o un intervalo para los importes probables, o bien si la tasa de actualización se estima en un intervalo.

3.2 Estimación probabilística del flujo de fondos

La estimación probabilística del flujo de fondos consiste en expresar los importes periódicos como un valor esperado, 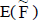, considerando explícitamente una distribución de probabilidad de cada uno de esos importes. Esta distribución se estima mediante simulación probabilística o considerando distintos escenarios.

a) Estimación con simulación aleatoria

Una forma de realizar la estimación probabilística es expresar las variables de los modelos que se formulan para el proyecto como variables aleatorias⁵, con distribuciones de probabilidad que las representan. A partir de esto se determina la distribución de probabilidad de los importes del flujo de fondos, .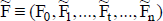

La distribución de probabilidad de cada importe se suele calcular con simulación aleatoria (o de Montecarlo), con muestras aleatorias simuladas de las variables que se consideran en el modelo del flujo de fondos. Este procedimiento fue descripto por David Hertz en 1964 (Hertz, 1964) como una metodología que desarrolló en McKinsey, y su uso se ha extendido al popularizarse los programas de simulación;⁶ se esquematiza en la figura 4.

Figura 4 Simulación y flujo de fondos

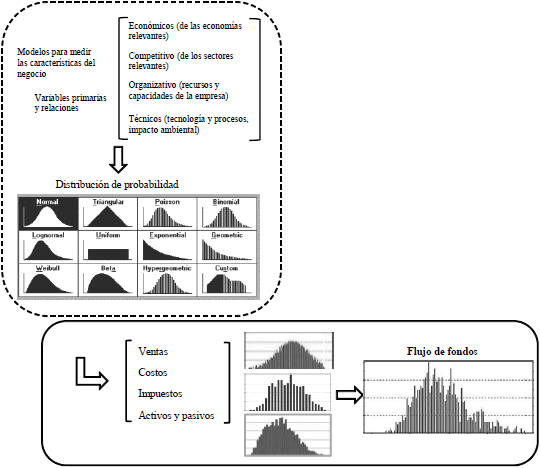
Los modelos que se usan para la estimación suelen requerir la consideración de dependencias entre las variables (la relación, según funciones económicas entre, por ejemplo, tamaño del mercado, participación, precio y esfuerzo comercial). En la estimación con simulación aleatoria se requiere especificar el grado de correlación entre las variables en cada período y en períodos sucesivos. Cabe mencionar que las variaciones en las muestras simuladas con las distribuciones que se usan pueden estar o no correlacionadas, ya que ésa es una información que se estima explícitamente⁷.

La estimación de la distribución de probabilidad de las variables a partir de las cuales se determina el flujo de fondos puede reflejar información que se describe de modo estadístico (por ejemplo, la distribución observada de precios, o de fallos o de productos defectuosos de una máquina, etc.). También puede basarse en otras evidencias, o en las creencias según la información del analista o experto. Esto último suele denominarse probabilidad subjetiva, para distinguirla de los fenómenos que se pueden describir con una distribución de las variaciones aleatorias observables (las "frecuencias")⁸.

Podría decirse, sin embargo, que todas las estimaciones de probabilidad son subjetivas, en el sentido de que se basan en la información disponible para quien las realiza. Esta información puede ser de frecuencias observadas, de características intrínsecas de un fenómeno (cuando se conoce la estructura de funcionamiento), de plausibilidad de un hecho, de consenso de opiniones, etc. A partir de esa información se infiere la distribución que se considera más representativa. Por eso, la calificación subjetivo no debe pensarse con el significado de arbitrario: se considera que, con similar información, varios individuos llegarían a la misma estimación de probabilidad.

Los grados de creencia pueden ser distintos según la información. Por eso se dice que, en el ámbito de las estimaciones para decisiones de negocios, la probabilidad no es la creencia de un lego, sino de alguien con conocimiento de aquello que se estima. De todos modos, la información suele ser incompleta o parcial. Esto tiene consecuencias, tanto en el significado del valor que se calcula como en la consideración explícita de la imprecisión de las estimaciones. En los puntos 4 y 5 se comentan estos aspectos.

b) Estimación con escenarios

La medición del valor esperado del flujo de fondos puede realizarse estimando los importes periódicos en diferentes configuraciones del futuro, que se denominan genéricamente estados (ver el esquema en la figura 5). Cuando los estados se reducen a una cantidad relativamente pequeña de perspectivas acerca del desenvolvimiento de la inversión se suelen designar como escenarios⁹.

Figura 5 Escenarios y flujo de fondos

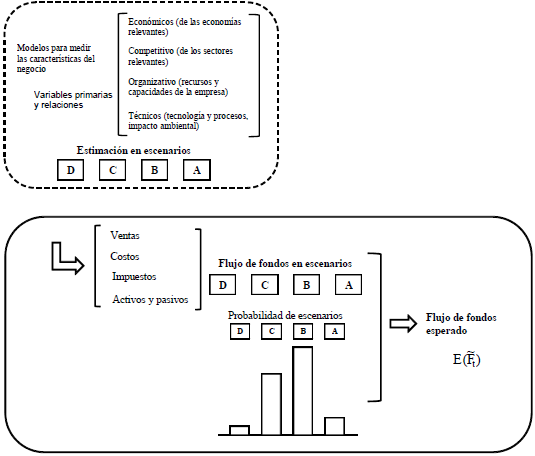
En cada una de estas perspectivas del futuro se estiman las variables del modelo del flujo de fondos. La estimación en cada escenario puede ser puntual, o mediante las distribuciones de probabilidad de esas variables (medidas, a su vez, con simulación de Montecarlo).

El flujo de fondos se expresa con el valor esperado de los importes, considerando una estimación de la probabilidad 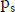del escenario s (que expresa el grado de creencia en la materialización de cada escenario). Los escenarios son, podría decirse, las variables aleatorias básicas de la estimación, y en cada escenario se reconoce la incertidumbre acerca de los importes periódicos, 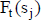¹⁰.

Con S escenarios considerados en la estimación, el importe esperado por período se determina con los importes estimados y la probabilidad de cada escenario:

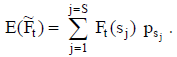En sentido estricto, la estimación en escenarios refleja perspectivas podría decirse, separables o discretas, acerca del futuro, por eso se consideran dos grupos de distribuciones de probabilidad: de las variables en cada escenario y de los escenarios.

La estimación de la distribución de probabilidad de los importes periódicos en un solo paso, con la distribución de las variables (tal como se describe en el apartado a anterior), refleja una situación de perspectiva única acerca del futuro (con una estimación de importes y variabilidad). Por eso, cuando la representación más adecuada del futuro requiere considerar esas características discretas, puede resultar difícil estimar distribuciones de probabilidad de las variables y sus relaciones de modo que se mida el valor esperado del flujo de fondos en un solo paso.

La referencia a escenarios, sin embargo, se ha difundido también para estimar el flujo de fondos en situaciones que son de perspectiva única (del estilo: "gran crecimiento", "crecimiento medio", "crecimiento bajo"). Se separa en unos pocos puntos algo que es continuo y único (crecimiento, precios, etc.) porque puede funcionar mejor como un recurso de comunicación. Este uso tal vez se origina en las connotaciones atractivas que tiene la expresión escenarios del negocio.

3.3 Estimación del flujo de fondos con números borrosos

a) Flujo de fondos borroso y desborrosificado

La estimación de las variables primarias que se consideran para el proyecto o el negocio puede expresarse con números borrosos (fuzzy numbers). Operando con éstos se obtienen los componentes del flujo de fondos (ganancia, impuestos, y activos y pasivos operativos) también como números borrosos. Con estos componentes se determina el número borroso de los importes periódicos, que se puede simbolizar 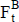(donde la B es por borroso; también se puede expresar 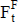, la F es por fuzzy), como se muestra en la figura 6.

Figura 6 Números borrosos y flujo de fondos

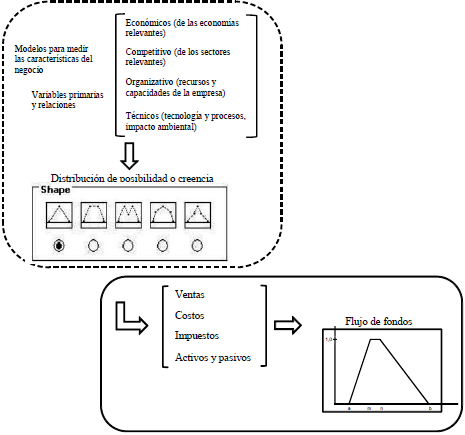
Para el uso en la valuación se obtiene una cifra 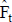de cada importe periódico del flujo de fondos mediante la desborrosificación (defuzzification) de los números borrosos calculados .

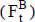Desborrosificar significa determinar un número preciso o nítido (crisp) con el que se representa a un número borroso. Genéricamente, la desborrosificación es una operación que se realiza para que los números borrosos puedan emplearse en instrucciones o algoritmos que requieren una magnitud única (no un intervalo). Por ejemplo, para la respuesta en un sistema de control, para ordenar o comparar números borrosos; o, en el caso de la valuación, para calcular un valor con una tasa ajustada por riesgo. Hay varios métodos de desborrosificación; los más simples son variantes de una media aritmética (denominados "centro de gravedad", o centroide, y "media de máximos")¹¹.

b) Comentarios acerca de los números borrosos

Los números borrosos son una generalización de los intervalos para la expresión de posibilidad o creencia acerca de algo. Un número borroso es una familia de intervalos que representan la estimación de una magnitud. Los números únicos (no borrosos, denominados precisos o nítidos, crisp) y los intervalos simples se pueden considerar casos especiales de números borrosos.

La aritmética borrosa (fuzzy arithmetic) es un cálculo con intervalos, que opera sobre números que se especifican según la noción que se tiene de la variable estimada. Entonces, la aritmética borrosa es un formalismo para realizar cálculos con cantidad numéricas que son conocidas imprecisamente (imprecisión que se expresa entre 0 y 1), y que se definen con una distribución unimodal que llega a la unidad para uno o varios valores.

La función de pertenencia de un número borroso se puede interpretar como una distribución de posibilidad. La posibilidad de algo es una medida de pertenencia a un conjunto. A diferencia de la probabilidad, la posibilidad no es distributiva en el conjunto pertinente: la suma de posibilidades (de, por ejemplo, la magnitud del flujo de fondos, o de los escenarios) es mayor que 1.

Los cálculos con números borrosos son relativamente simples (si se usa alguno de los programas de computación disponibles para realizar las operaciones). En el apéndice 2 se comentan los detalles y se describen formalmente las operaciones aritméticas.

El cálculo con intervalos supone que las variables con las que se opera están totalmente correlacionadas (es equivalente a decir, en una estimación probabilística, que el coeficiente de correlación es 1 cuando se suman o multiplican intervalos, y es -1 cuando se restan o dividen). Por esto, el resultado que se obtiene es un intervalo más amplio (señal de más incertidumbre), en comparación con el que reflejaría una situación con correlación menor, o sin correlación¹².

Finalmente, a veces se dice que los cálculos con estimaciones que se expresan con números borrosos son una aplicación de la lógica borrosa (fuzzy logic, también denominada lógica difusa)¹³. Los cálculos con estimaciones borrosas, para muchos tipos de análisis económicos y técnicos (entre ellos la valuación), se encuentran presentados con ese rótulo, que no es estrictamente correcto: lo que se aplica es la aritmética borrosa¹⁴.

c) Probabilidad, posibilidad y tipos de incertidumbre

La teoría de posibilidad¹⁵ y las mediciones borrosas se suelen plantear como una forma de tratar las situaciones de imprecisión que es más adecuada que la teoría de probabilidad. Se dice que ésta se relaciona con la incertidumbre aleatoria (propia de la estructura de un fenómeno), mientras que la posibilidad se refiere a la incertidumbre epistémica (originada en el conocimiento incompleto o parcial)¹⁶.

Las funciones de posibilidad se presentan como análogas de las funciones de probabilidad, y se dice que deberían usarse cuando la incertidumbre se origina en la imprecisión de la situación y no en la aleatoriedad. La imprecisión puede ser directamente cuantitativa o lingüística. La primera se trata en la teoría de posibilidad cuantitativa (de Dubois y Prade), y la segunda (que se denomina vaguedad) se trata específicamente en la teoría de conjuntos borrosos y de posibilidad (de Zadeh)¹⁷.

La teoría de posibilidad y la teoría de probabilidad son dos formas con las que se puede reflejar la propagación de la incertidumbre de las estimaciones, hasta llegar a la medida resultante (que, en la valuación, es el flujo de fondos y la tasa de actualización). Entonces, se dice que puede hacerse una representación borrosa de la imprecisión o una representación probabilística de la variación.

Esta distinción, sin embargo, no es tan nítida como puede parecer en el enunciado. Las estimaciones con forma probabilística pueden reflejar tanto la incertidumbre estrictamente aleatoria como la imprecisión por deficiencias de información, y también se pueden expresar así las estimaciones referidas a acontecimientos que no son repetitivos en el sentido de disponer de una distribución de frecuencias¹⁸.

La formalización de la teoría de posibilidad y la expansión formal de la teoría de probabilidad a las situaciones de imprecisión se han producido juntas en los últimos veinte años, y pueden verse como un movimiento hacia conceptos y herramientas más finos para tratar la incertidumbre¹⁹.

4. Estimación puntual del valor de un proyecto

Sea que los importes se estimen con una expresión probabilística o con números borrosos, no existen diferencias en la forma en que se realiza la valuación con el flujo de fondos actualizado. El resultado no es un valor probabilístico o un valor borroso, respectivamente, sino que se obtiene lo que la valuación dice en su nombre, una estimación de valor.

Pueden existir estimaciones de valor en un intervalo, pero esto no depende estrictamente de una u otra forma de expresar la medición del flujo de fondos.

Un aspecto esencial es el alcance de la tasa de actualización que se emplea, y específicamente la compensación por riesgo que incluye. La relación entre el riesgo del negocio y esta compensación evoca el tema de la información que subyace en la estimación del flujo de fondos y en los rendimientos de mercado.

Un defecto de información que produce estimaciones muy imprecisas es un "riesgo" que no estaría compensado en la tasa requerida por usuarios informados. El grado de diferencia en la base de información, sin embargo, no queda mejor reflejado en estimaciones borrosas en vez de probabilísticas: no se refiere a la imprecisión y su tratamiento, sino a la relación entre la imprecisión de la estimación del flujo de fondos y la tasa de actualización.

4.1 Valuación con estimaciones probabilísticas

Con la expresión probabilística de las estimaciones se determina la distribución de probabilidad del flujo de fondos, que se describe con la magnitud esperada 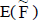y alguna medida de variabilidad (por ejemplo, el desvío estándar). Esto puede reflejar una medición mediante simulación aleatoria o con escenarios.

El valor se calcula actualizando el valor esperado de esos importes periódicos, 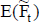(figuras 7 y 8). Si la tasa de actualización se estima de modo puntual²⁰, el valor es:

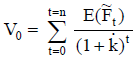Ecuación 3

Figura 7 Valuación con flujo de fondos simulado

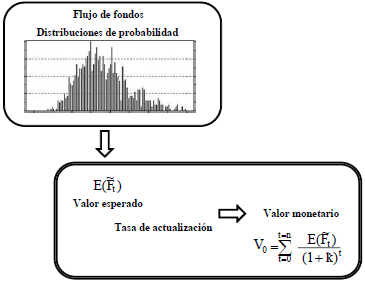
Figura 8 Valuación con flujo de fondos en escenarios

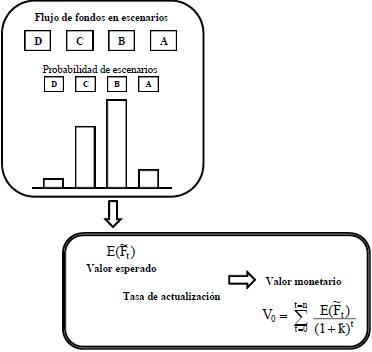
Este valor de la inversión es una estimación puntual del valor del proyecto o el negocio, considerando que la incertidumbre acerca del flujo de fondos está compensada con la tasa ajustada por riesgo que se emplea.

De modo preciso, al valuar estimando la distribución de probabilidad del flujo de fondos no se obtiene una distribución de probabilidad del valor de la inversión, ni un posible rango del valor, sino una medida estimada puntual del valor. El valor de la inversión con el flujo de fondos esperado no es un valor esperado.

La incertidumbre que se expresa en las distribuciones de probabilidad de las variables con las que se estima el flujo de fondos puede implicar que los importes periódicos se distribuyan en un rango bastante grande. Pero esto no significa que la estimación del precio de ese flujo de fondos se realice con un rango de similar amplitud relativa. Esa variabilidad del flujo de fondos está compensada por la tasa ajustada por riesgo, y por eso puede hacerse una afirmación estrictamente puntual acerca del valor.

Por ejemplo, si el flujo de fondos se estima en un rango entre $ 40 y $ 100 por período, con un valor esperado de $ 75, y si la tasa que corresponde a ese nivel de riesgo es 10% anual, la estimación del valor de un flujo perpetuo de esa magnitud es $ 750 (= 75 ÷ 0,10). Justamente por esta característica del valor que se calcula de una inversión es posible realizar comparaciones del valor de varias alternativas de inversión.

Decir que el valor (el precio de ese flujo de fondos) puede ser hoy entre $ 400 y $ 1.000 no sólo es erróneo, sino que además puede generar perplejidad en el destinatario, que puede considerar, por la amplitud del rango, que la valuación realizada es muy poco informativa.

Parece prudente poner énfasis en este aspecto porque existe una propensión, al calcular el valor con el flujo de fondos que se obtiene mediante simulación aleatoria, a referirse al valor esperado y a la variabilidad (desvío estándar) de ese valor, y a realizar afirmaciones probabilísticas acerca del valor. Esto no es consistente, ni conceptual ni prácticamente, con el uso en la valuación de una tasa ajustada por riesgo. En el punto 6 se comentan algunos aspectos de esta práctica.

Por la mecánica del cálculo (mediante simulación o aritmética probabilística, o a partir del flujo de fondos en escenarios) se puede determinar una distribución del valor de la inversión con las distribuciones de los importes periódicos. Pero esto no significa que el valor se estime en el rango que resulta de esa distribución.

Si se realiza ese cálculo, y se determina una "distribución de probabilidad del valor" con la distribución de los importes periódicos, las afirmaciones probabilísticas se refieren al flujo de fondos, y sólo indirectamente al valor. Se puede decir, por ejemplo, que hay una probabilidad p de que el flujo de fondos tenga una magnitud tal que el valor (considerando la incertidumbre que se enfrenta y cuyo impacto se refleja en la tasa 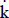ajustada por riesgo) sea menor que un importe específico.

En el ejemplo simplificado, con una estimación del flujo de fondos en el rango entre $ 40 y $ 100 por período, con un valor esperado de $ 75, y una tasa ajustada por riesgo de 10%, se puede decir que hay una probabilidad 0,2 de que el valor de ese flujo de fondos sea menor que $ 500.

Se interpreta de igual manera una afirmación probabilística referida a que el valor actual neto de un proyecto sea negativo.

La misma precaución se requiere en la interpretación de las cifras de valor en los escenarios que se consideran. Para transmitir una dimensión distinta del riesgo puede ser útil decir que en el "peor" escenario el valor es, como en ese ejemplo, $ 400. Esa dimensión se refiere al impacto que podría tener, en la situación de la empresa o del inversor, el que se manifieste efectivamente un escenario de resultados muy negativos. Por ejemplo, en tal situación un proyecto podría comprometer la continuidad de la empresa, o bien afectar significativamente su estrategia competitiva o financiera. Ese impacto, que depende de la magnitud del proyecto en relación con el tamaño de la empresa, no tiene una relación directa con la valuación que se considera aquí, sino que es un aspecto que interviene en la ponderación del valor como uno de los elementos de la decisión de inversión.

De todos modos, para que la afirmación acerca del valor en el peor escenario tenga la fuerza comunicacional que se pretende es necesario disimular su fundamento probabilístico.

Por una propiedad matemática (de la suma y la multiplicación), el valor del proyecto se puede calcular con el valor en cada escenario ponderado por la probabilidad de escenarios, o con el flujo de fondos esperado según la probabilidad de los escenarios.

Expresado con la formulación del apartado 3.2, si el valor esperado del flujo de fondos, con los importes y las probabilidades de los escenarios, es 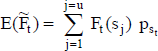, se cumple que

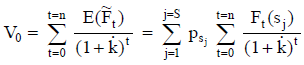El valor en cada escenario (en el lado derecho de la ecuación) no puede verse de modo aislado, ya que es tal considerando toda la distribución de probabilidad de los escenarios. Y esta distribución es consistente con la tasa de actualización ajustada por riesgo que se emplea en el cálculo.

4.2 Valuación con estimaciones borrosas

Con la estimación del flujo de fondos como números borrosos, el valor del proyecto o el negocio se calcula con la cifra desborrosificada 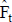de cada importe 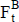(figura 9). Con una estimación puntual de la tasa de actualización que compensa el riesgo por las características del proyecto o el negocio, el valor se determina:

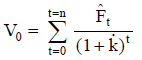Ecuación 4

Figura 9 Valuación con flujo de fondos borroso

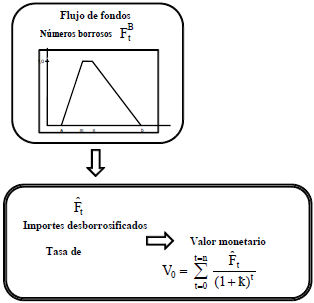
En el apéndice 3 se ejemplifica la valuación con las estimaciones expresadas con números borrosos. Se plantea el proyecto de inversión EME, cuyas estimaciones se resumen en números triangulares de los importes periódicos. En ese ejemplo la tasa de actualización también se estima con números triangulares (según lo que se explicará en el punto 5).

Si se desborrosifica tanto el flujo de fondos como la tasa, considerando el promedio, se obtiene que el valor actual neto es $ 382. También puede pensarse que es más representativo considerar que las cifras desborrosificadas son las de máxima posibilidad (el modo de los números triangulares). Entonces, el valor actual neto se estima en $ 359.

La diferencia es equivalente a la que existe al trabajar con el valor esperado o con el valor modal de una distribución de probabilidad²¹. Si se considera que esas estimaciones son distribuciones triangulares de probabilidad (en vez de números borrosos), y se realiza un cálculo con simulación de Montecarlo, se obtiene un resultado similar²².

Cuando se consideran explícitamente varias perspectivas de futuro (estados o escenarios), las estimaciones borrosas del flujo de fondos se realizan para cada escenario, y se opera con ellas considerando una distribución de posibilidad de los escenarios²³. Se considera que el importe periódico esperado (en el sentido probabilístico) es la cifra desborrosificada con la que se calcula el valor.

Para esto, la distribución de posibilidad se convierte en una distribución aditiva equivalente. Por ejemplo, se puede estimar las siguientes posibilidades para los escenarios que se consideran (del "peor" al "mejor"):

Los escenarios "extremos" tienen baja posibilidad, y se considera que uno de los escenarios intermedios, el B, es de máxima posibilidad. Como la posibilidad es una medida no aditiva, para operar se estandariza con la suma de las posibilidades (en este ejemplo, 2,5).

De modo análogo a lo que se menciona en el apartado 4.1 para la expresión probabilística de los escenarios, se puede calcular un valor en cada escenario con el flujo de fondos desborrosificado de ese escenario. Esto puede ser un recurso comunicacional para referirse al valor en el peor o en el mejor escenario, pero el intervalo completo de estos valores no es la expresión de un valor borroso.

Valuación con flujo de fondos desborrosificado y valor desborrosificado. La noción básica es que el valor que se calcula con una estimación borrosa del flujo de fondos no es un número borroso.

Por las mismas razones mencionadas, no parece correcto determinar un "valor borroso" a partir del rango completo de los números borrosos que se calculan para representar el flujo de fondos de la inversión o el negocio. Tal proceder no sería compatible con el uso de una tasa ajustada por riesgo para la valuación. Insistir en este aspecto puede parecer exagerado si no fuera porque se ha planteado, en muchos estudios, que la valuación de un proyecto de inversión a partir de estimaciones con números borrosos produce un "valor borroso" (fuzzy net present value). Las características de estas formulaciones se comentan en el apartado 6.2.

Consideremos el proyecto EME (cuyo cálculo se explica en el apéndice 3). El proceder mencionado implicaría informar que el valor actual neto del proyecto está entre una cifra negativa de $ 224 y un valor positivo de $ 1.046. El valor de máxima posibilidad, como se mencionó, es $ 359.

Esos extremos de muy baja posibilidad pueden tener algún contenido informativo, y son equivalentes a determinar el peor y el mejor resultado²⁴. Pero, como información del valor estimado del proyecto, concluir que puede estar entre -224 y 1.046 parece un rango muy amplio; alguien podría decir que es como informar la temperatura que se pronostica para el mediodía en una ciudad diciendo que puede estar entre 5°C y 40°C.

No todos los estudios relacionados con las estimaciones borrosas plantean como resultado final un valor borroso. Por ejemplo, Lin y Lee (2010) desarrollan el cálculo del valor borroso de un proyecto, y usan ese resultado para un indicador desborrosificado que se pondera con factores estratégicos para obtener un puntaje del proyecto.

Yao, Chen y Lin (2005), al plantear un modelo para la valuación con el flujo de fondos actualizado borroso (fuzzy discounted cash flow, FDCF), consideran explícitamente una "tasa que refleja el riesgo estimado del flujo de fondos" o "tasa de rendimiento requerido" de los inversores. El modelo que desarrollan obtiene el valor mediante la desborrosificación del valor en el período de pronóstico específico y valor de continuación, los dos componentes que suelen usarse en las valuaciones.

Es decir, calculan el valor como un número borroso a partir de los componentes expresados de esa forma, y este número después se desborrosifica. Posiblemente, en la mayoría de los casos, no existirán diferencias significativas entre este resultado y el que se plantea aquí: desborrosificar los importes periódicos y con ellos calcular el valor.

Sin embargo, este último procedimiento presenta ventajas operativas y comunicacionales. ¿Para qué buscar expresiones, a veces bastante complicadas, para "borrosificar" el valor a partir de un flujo de fondos borroso, si esta "borrosificación" no es necesaria cuando se usa una tasa de actualización ajustada por riesgo?

4.3 ¿Qué riesgo está compensado en la tasa ajustada por riesgo?

Un aspecto a considerar en la valuación con una tasa ajustada por riesgo es la relación entre la incertidumbre del flujo de fondos y la compensación en la tasa de actualización. Como la valuación es una estimación del precio del flujo de fondos si se transara en el mercado de títulos, la primera respuesta es que la tasa de actualización compensaría el riesgo sistemático al que está expuesto el flujo de fondos. Por esto, se dice que debe considerarse esa compensación según la diversificación accesible en el mercado de referencia, y la tasa de actualización se estima con el rendimiento de mercado requerido para ese flujo de fondos.

Para proceder de este modo, la estimación del flujo de fondos debe reflejar expectativas acerca de la economía y el sector que sean congruentes con las que se manifiestan en los precios de los títulos. Este sería el conjunto de información con respecto al cual son condicionales los rendimientos esperados.

Puede pensarse que ésas son expectativas de consenso, o intersubjetivas, acerca de las variables económicas relevantes y la probabilidad de los estados futuros. Esto no implica suponer conocimiento completo de la distribución de probabilidad que, podría decirse, rige la realización de los estados futuros. Se considera que el rendimiento del mercado de títulos incluye una compensación por el riesgo de que ocurra uno u otro estado, y una compensación por la ambigüedad, o conocimiento parcial acerca de la distribución de probabilidad de los estados²⁵.

Cuando las estimaciones del flujo de fondos de un proyecto o un negocio se basan en menos información que la que podría usarse con un análisis más cuidadoso, la imprecisión de esas estimaciones posiblemente no esté compensada en la tasa de rendimiento del mercado. Tal imprecisión se puede referir tanto a los factores que se consideran principalmente sistemáticos como a los factores que se relacionan más con riesgos diversificables.

En ese caso la valuación sería imprecisa (existiría un rango relativamente amplio de valor). Pero es difícil determinar de modo cuantitativo ese rango, porque es el propio juicio el que se basa en información excesivamente incompleta. Juzgar la propia imprecisión, en tal situación, implica saber lo que se manifiesta que no se sabe.

Hay dos consideraciones prácticas que disminuyen la importancia de este aspecto (la amplitud de la imprecisión y su relación con el rendimiento de mercado)

1) Como se ha mencionado, las estimaciones para la valuación reflejan la opinión de expertos o analistas, y por eso podría pensarse que no tienen un nivel tan alto de imprecisión.

2) Uno de los aspectos en que se basa la distinción entre incertidumbre aleatoria e incertidumbre epistémica es que esta última puede reducirse más que la primera con la obtención de más información. En el caso de la incertidumbre aleatoria, con más información sólo puede mejorarse la estimación de la distribución de probabilidad hasta el límite de la variabilidad intrínseca (se mejora la estimación de la distribución de probabilidad). Por eso se afirma que la evaluación de la incertidumbre debería orientarse a determinar hasta qué punto es recomendable reducir la imprecisión con más información (éste es, podríamos decir, el auténtico análisis de riesgo de una inversión).

En función de esto, parece adecuado considerar que las estimaciones referidas al proyecto o negocio son congruentes con el contenido informativo de la tasa de actualización del mercado. Entonces, la tasa que se emplea compensa los riesgos relevantes, y el valor que se calcula con ella no es una magnitud que quede descripta con una distribución de probabilidad o con un número borroso. Es, como se ha comentado, una estimación que puede expresarse de modo puntual, o bien en un intervalo, con las características que se mencionan en el punto siguiente. Esta última situación puede considerarse que es de ignorancia parcial razonable, una simplificación consciente que permite enunciar sus propios límites (a diferencia de lo mencionado antes con respecto a la imprecisión).

5. Estimación del valor en un rango

En la valuación de proyectos o negocios es frecuente que el resultado se exprese en un rango o intervalo, con el que se reconoce la imprecisión de las estimaciones en que se basa la cifra estimada de valor.

Si se trabaja con el flujo de fondos esperado y una medida puntual de la tasa de actualización, la forma más simple (aunque con poco fundamento) es determinar un rango con una medida estandarizada del posible error en la estimación: el intervalo se forma considerando el valor calculado +/- 3%, por ejemplo (o +/- 5%).

Esto implica suponer que las estimaciones son razonablemente ajustadas, ya que expresan la opinión de expertos en el tema; el rango busca transmitir la noción de que hay una imprecisión que es irreductible, aún con el trabajo de expertos.

Una forma más elaborada de expresar la estimación de valor en un rango se basa en considerar de modo explícito la imprecisión de la estimación del flujo de fondos y de la tasa de actualización. Ambos aspectos se comentan a continuación, con referencia a la expresión probabilística y a las mediciones borrosas.

5.1 Valuación con una tasa de actualización que se estima en un intervalo o como variable aleatoria

Puede ser adecuado expresar la estimación de la tasa de actualización en un intervalo, o con una distribución de probabilidad (también, como se considera en el apartado 5.3, con un número borroso). Esto reflejaría la incertidumbre acerca de cuál es la tasa de actualización que corresponde al riesgo del flujo de fondos estimado. Si se tienen en cuenta las modalidades más usuales para estimar la tasa de actualización, que aparezca este tipo de duda es algo bastante razonable.

En este caso, la estimación de valor no será puntual (la "mejor" medida del valor que puede hacerse con la estimación que se realiza del flujo de fondos y la tasa de actualización), sino que hay alguna forma de variabilidad en torno al valor esperado. Es claro que la magnitud de esta variabilidad depende de la incertidumbre acerca de la tasa, y no de la variabilidad del flujo de fondos (que está compensada en la tasa de actualización ajustada por riesgo).

La tasa puede expresarse en un intervalo (o, en términos probabilísticos, con una distribución uniforme) o con una distribución de probabilidad de otro tipo (por ejemplo, triangular)²⁶. La variabilidad, o el rango de estimación del valor, se expresa según la distribución de la tasa de actualización.

Volvamos a considerar el ejemplo simplificado que se comentó en el apartado 4.1: un proyecto con un flujo de fondos entre $ 40 y $ 100 por año, con valor esperado de $ 75; con una tasa de actualización estimada de 10%, el valor es $ 750. Si la tasa se estima entre 9,5% y 10,5%, el valor podría medirse en el rango entre $ 714 (= 75 ÷ 0,105) y $ 790 (= 75 ÷ 0,095).

El valor esperado y la variabilidad del valor de la inversión se pueden calcular mediante simulación probabilística, actualizando el valor esperado de los importes periódicos con el factor de actualización según una muestra simulada de la tasa para cada período. Con el desvío estándar de esa simulación del valor se puede expresar un rango para el valor de la inversión.

El factor de actualización del importe de cada período se determina acumulando los factores que resultan de la simulación de la tasa en cada uno, ya que aunque la distribución de la tasa se estime igual en todos los períodos, la simulación implica una situación de tasas distintas en cada período. Puede ser práctico considerar que las tasas en cada período son estocásticamente independientes; de lo contrario, hay que reconocer una correlación serial²⁷.

Si los parámetros de la distribución de la tasa son un límite inferior y uno superior (como ocurre con las distribuciones uniforme o triangular), el rango para el valor se puede aproximar con el valor según esos parámetros de la tasa de actualización.

En una estimación con distribución uniforme 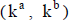, el valor está entre los extremos 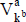y 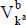. Si la distribución es triangular 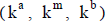, también se expresaría un "valor modal" del valor, 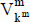, con el parámetro modal de la distribución.

Entonces, la variabilidad del valor es consecuencia de la incertidumbre acerca de la tasa de actualización que compensa la variabilidad estimada del flujo de fondos, pero no directamente de esta última.

Estas expresiones de valor en intervalos se reducen a una cifra única para realizar comparaciones de valor (cuando se requieren). Para esto se usa la cifra media del intervalo, o el valor con la estimación modal de la tasa.

5.2 Reconocimiento probabilístico de la imprecisión en la estimación del flujo de fondos

Algunas de las estimaciones que se usan en la valuación se pueden realizar a partir de un conjunto razonable de evidencia; en ese caso, la expresión probabilística de las variables tiene un sentido más cercano a la denominada incertidumbre aleatoria.

La estimación de muchas de las variables, sin embargo, se realiza a partir de información menos amplia; las distribuciones de probabilidad de algunas variables, y de los escenarios, suelen reflejar incertidumbre epistémica, originada en el conocimiento incompleto de aquello que se estima.

Es razonable pensar que la imprecisión es una característica general que tienen las estimaciones (tanto económicas como técnicas) que se usan para la valuación. En estos casos, considerar que se puede reflejar ese conocimiento en la estimación de una distribución de probabilidad para cada variable puede ser una condición poco realista.

En los últimos veinte años se han formulado varias teorías para representar estas situaciones de imprecisión²⁸. La expresión probabilística toma alguna forma de intervalo para las distribuciones de probabilidad, según la evidencia disponible o las creencias subjetivas o de consenso acerca de la situación²⁹.

El rango de imprecisión se puede aproximar mediante simulación. Una forma simplificada es obtener la estimación del flujo de fondos considerando dos conjuntos de distribuciones de probabilidad de las variables (se podría decir que se consideran dos "escenarios por imprecisión"), y usar el flujo de fondos esperado en cada caso como límites del intervalo de estimación.

También se puede aplicar la técnica de simulación con distribuciones cuyos parámetros se estiman en un intervalo (Kreinovich, Beck, Ferregut, Sanchez, Keller, Averill y Starks, 2004). Otra forma, más complicada operativamente, es realizar la simulación con distribuciones de probabilidad de los parámetros de las distribuciones de las variables (Hoffman y Hammonds, 1994; Hattis y Burmaster, 1994). Este tratamiento de la incertidumbre paramétrica se conoce como método de Montecarlo de segundo orden (Second-order Monte Carlo simulation, SOMCS), y consiste en simulaciones anidadas, aunque se puede expresar el conjunto como una simulación de primer orden.

En lugar de simulación, se puede considerar la incertidumbre de las variables con un intervalo de distribuciones (es decir, los parámetros se estiman en intervalos), y calcular los límites de probabilidad (probability bounds). Es el método denominado de las "cajas de probabilidad" (P-boxes), por la forma gráfica que tiene el resultado (figura 10). El tamaño de la "caja" (el intervalo del valor esperado) depende de la correlación entre las variables que se consideran³⁰.

Figura 10 Límites de probabilidad

Es claro que estas formas más elaboradas de operar con las estimaciones tienen sentido si el modelo para obtener el flujo de fondos se formula con varios niveles, y la imprecisión se relaciona con las variables más básicas (económicas o técnicas). En tales casos, la forma en que se propaga esa incertidumbre hasta los componentes del flujo de fondos puede ser importante.

Si, por el contrario, el modelo tiene pocos niveles, la medición probabilística más sofisticada proporciona únicamente una ilusión. Por ejemplo, cuando sólo se estiman los componentes del flujo de fondos del proyecto o el negocio (ventas, costos, impuestos, activos y pasivos), se obtienen cifras cuya calidad en poco difiere de una estimación directa de intervalos simples.

Con alguna de estas variantes se obtiene el rango de valor esperado del flujo de fondos, y se calcula un rango de valor del proyecto. Este rango es distinto al rango completo de la distribución de probabilidad del flujo de fondos (y debería ser significativamente menor).

El valor en ese rango se calcula con la tasa ajustada por riesgo. Para interpretar esto hay que considerar que la tasa compensa el riesgo que se manifiesta en la distribución del flujo de fondos, pero no la imprecisión en la medida del propio parámetro, el valor esperado del flujo de fondos. Al estimar un intervalo para los importes periódicos esperados, se puede pensar que se abre una brecha en la estimación, una indeterminación de origen epistémico que, en la valuación, no está compensada por la tasa de actualización que se emplea.

Si ese rango es muy amplio, significa que la información disponible no permite una estimación muy adecuada del valor. Como esa amplitud se origina en incertidumbre epistémica, es posible reducirla con más información o con mejores juicios expertos.

5.3 Tasa de actualización como número borroso e intervalo de valor de máxima posibilidad

Consideremos el caso en que la tasa de actualización se estima como un número borroso 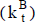³¹. Entonces, el valor que se calcula con el importe periódico desborrosificado, 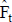, y esa tasa borrosa, es un número borroso.

En el ejemplo que se comenta en el apartado 4.2 (ver apéndice 3) se considera el proyecto EME, con estimaciones triangulares del flujo de fondos y de la tasa de actualización. Vamos a operar con el flujo de fondos desborrosificado, pero reconociendo en el valor la imprecisión con que se estima la tasa.

Si los importes periódicos se desborrosifican con el promedio, el valor actual neto se estima entre $ 349 y $ 420, con $ 379 como máxima posibilidad. La estimación se expresa como un número triangular porque la tasa de actualización está medida de ese modo.

Al considerar como importe periódico el de máxima posibilidad, el VAN es [329, 359, 398]. La diferencia con el cálculo anterior es atribuible a la pequeña asimetría hacia el extremo superior de los importes en algunos períodos.

El rango de la tasa de actualización expresa la imprecisión acerca de cuál es la tasa que compensa la incertidumbre del flujo de fondos. Por eso, es razonable operar explícitamente con la borrosidad de la tasa, pero no con la borrosidad del flujo de fondos.

En el ejemplo EME se considera que los importes son números borrosos triangulares, y por eso hay una sola cifra de máxima posibilidad. Esto ocurre si todas las variables primarias con las que se calculan los componentes del flujo de fondos son números triangulares.

Lo más frecuente es que algunas estimaciones sean rectangulares o trapeciales, además de triangulares (e incluso con otras formas, lineales o no lineales). En estos casos, los importes periódicos tienen una forma aproximada trapecial (según cómo se opere con los α-cortes, ver apéndice 2) y existe un intervalo de máxima posibilidad.

El valor que se calcula con ese intervalo, y una tasa estimada con forma triangular, es un número borroso trapecial.

En el ejemplo ENE (que se desarrolla en el apéndice 3) se expresa la estimación del flujo de fondos con números trapeciales. Operando con la tasa y el intervalo de máxima posibilidad de los importes periódicos se obtiene el valor actual neto como número borroso [223, 238, 286, 307]. El intervalo de máxima posibilidad del valor resulta del intervalo del flujo de fondos y la tasa de máxima posibilidad, y los extremos ($ 223 y $ 307) están influidos por los extremos de la tasa.

Figura 11 Valor borroso de dos proyectos

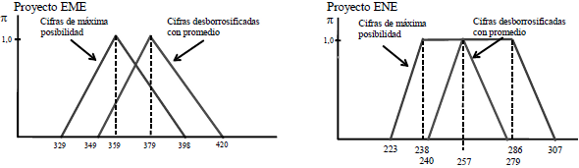
Ese intervalo del valor (entre $ 238 y $ 286) puede interpretarse de modo similar a lo que resulta de usar para el cálculo los límites de probabilidad comentados en el apartado anterior. Estos límites reflejan la imprecisión acerca de la distribución de probabilidad más representativa; como los límites se estiman con dos distribuciones posibles, el valor esperado de estas distribuciones sería equivalente a los extremos de máxima posibilidad de los números borrosos trapeciales.

La conclusión es que, en ambas formas de calcular el valor (con intervalos probabilísticos o de máxima posibilidad), la estimación expresa el grado de imprecisión de las cifras que se consideran más representativas del proyecto o negocio que se valúa.

Claramente no es toda la incertidumbre acerca de las cifras del negocio, sino lo que puede verse como una indeterminación acerca de las que serían las cifras más representativas; es expresar que hay una indeterminación irreductible en esa valuación, por la forma en que se realiza y/o por la información disponible.

El intervalo de valor que se calcula es lo más parecido a un valor auténticamente borroso. Auténtico en el sentido de que resulta de la brecha, o imprecisión central con que se representa la incertidumbre para la valuación. Es decir, es un número borroso que no es sólo consecuencia de realizar operaciones con las expresiones numéricas borrosas del flujo de fondos.

Las operaciones que se realizan con los números borrosos completos del flujo de fondos son inconsistentes con el uso de una tasa de actualización ajustada por riesgo. Esta inconsistencia existe tanto en la noción de valor probabilístico como en la noción que se suele proponer de un valor borroso.

6. El valor como valor esperado en un momento futuro

La valuación es la estimación del precio que tiene (o tendría si fuera transado) el flujo de fondos que se considera para un proyecto o negocio. Esa estimación se suele referir al precio en el momento presente. En las secciones anteriores se ha considerado el significado que tiene la estimación obtenida a partir de medidas probabilísticas o borrosas del flujo de fondos, con la forma de un estimado puntual o de un rango de valor.

Se ha enfatizado que, al calcularse con una tasa de actualización ajustada por riesgo, la medida puntual de valor no es un valor esperado (en el sentido probabilístico). Y que la medida de valor en un rango (o intervalo) resulta de la imprecisión que se reconoce en la estimación de la tasa de actualización o de la distribución de probabilidad de los importes periódicos. Pero ese rango no depende de la distribución completa de probabilidad de los importes periódicos, ya que el riesgo que muestran está compensado, en la valuación, con la tasa ajustada por riesgo.

En algunos tipos de análisis financiero se usan estimaciones del precio que tendría un proyecto o negocio en un momento futuro. Un caso es la estimación del precio, al final del período explícito de pronóstico, del flujo de fondos posterior al mismo (es el denominado valor de continuación o valor terminal).

Otro caso es la estimación del precio de un negocio al cabo de un determinado tiempo, en diferentes estados futuros. Esta medición se realiza para considerar el efecto de decisiones que podrán tomarse en un momento futuro, según la configuración de los estados y el valor en cada uno. Típicamente, la valuación en el momento presente se basa en alguna forma de reconocer las trayectorias y su probabilidad, hasta cada momento. Es, de modo genérico, la perspectiva de valor de las opciones reales, valor que se determina con árbol de decisiones, con programación dinámica, o con otros enfoques de valuación³².

El valor estimado en un momento futuro es claramente un valor esperado (con una distribución de probabilidad) o caracterizado como un número borroso. Ese valor se determina con los importes periódicos estimados para los períodos posteriores al momento al que se refiere el valor.

Digamos, para concretar la noción, que el período de estimación explícita que se considera es tres años y que el valor al fin de ese lapso se calcula con el flujo de fondos estimado a partir del año 4. Esa cifra se determina con la tasa ajustada por riesgo pertinente, que compensa la incertidumbre que afecta a esos importes periódicos. Pero el valor así calculado es, en el momento presente, un valor esperado: está influido por la incertidumbre entre este momento y el momento futuro de referencia (en el ejemplo, el fin del año 3).

El valor en un momento futuro es un valor esperado no por la incertidumbre posterior al momento de referencia (que está compensada con la tasa ajustada por riesgo que se usa) sino por la incertidumbre que existe entre el presente y el momento de referencia.

Tal valor (o precio futuro estimado) se considera en el cálculo de valor en el momento presente mediante alguna forma de actualización que reconoce el riesgo durante ese lapso. Por ejemplo, el valor de continuación se introduce en la valuación considerando la tasa ajustada por riesgo aplicable al lapso entre el momento presente y el momento de referencia. Como se ha explicado, es una estimación puntual del valor en el momento presente; o bien se expresa en un rango que reconoce la imprecisión de las estimaciones que se emplean.

En el caso de la valuación de opciones reales, el cálculo del valor en el momento presente se realiza con el valor en los momentos futuros y alguna forma de reconocer el riesgo en el lapso entre el presente y esos momentos (según sea el tipo de riesgos que se estimen, se considera un ajuste en la tasa de actualización o en el flujo de fondos). Por ejemplo, la posibilidad de realizar una inversión al cabo de dos años se evalúa considerando el valor en ese momento, en cada estado (ese valor es una estimación del precio en ese momento y ese estado, que puede hacerse con el flujo de fondos posterior y la tasa ajustada por riesgo pertinente). Con la probabilidad de estado (o escenario) se determina el valor esperado en el año 2; según el modelo que se considere, para esto pueden usarse probabilidades ajustadas (probabilidad neutral al riesgo, ver apéndice 1). En ese caso, el valor en el momento presente se calcula con la tasa sin riesgo como tasa de actualización.

Como conclusión, el valor en un momento futuro, como cualquier estimación con esa referencia temporal, es un valor esperado (en el sentido probabilístico) o un valor borroso (según la borrosidad de las variables que se consideran hasta ese momento futuro). Pero no lo es por las características de la estimación del flujo de fondos en que se basa ese valor (los importes posteriores al momento de referencia), sino por la incertidumbre hasta el momento en que comienza ese flujo de fondos estimado. El carácter de esperado del valor se origina en la incertidumbre acerca de los estados en el momento futuro de referencia, y no en la incertidumbre de lo que ocurrirá después (ya que eso está compensado con la tasa ajustada por riesgo).

7. El significado de un valor probabilístico y un valor borroso

7.1 El análisis basado en un valor probabilístico

a) Análisis de riesgo con una distribución de probabilidad del valor

Se suele denominar "análisis de riesgo de un proyecto de inversión" a la evaluación basada explícitamente en una distribución de probabilidad del valor, distribución que se determina a partir de una estimación probabilística del flujo de fondos. Con esa distribución se calcula, por ejemplo, la "probabilidad de pérdida" (valor actual neto negativo) (figura 12), y se puede comparar la variabilidad de la distribución del valor de dos o más proyectos (expresado gráficamente, según la forma de las distribuciones acumuladas y su posible cruzamiento)³³.

Figura 12 Distribución de valor: Uso incorrecto de las estimaciones probabilísticas

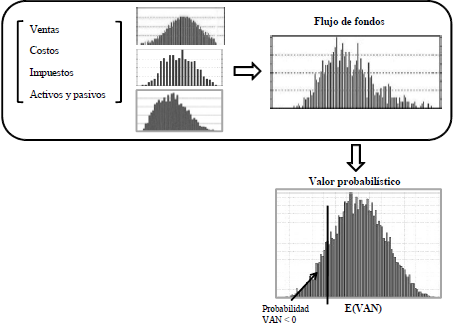
Por lo general, en ese tema no se comentan distinciones acerca de la tasa de actualización con la que se calcula el valor que tendría esa distribución y, también habitualmente, se usa una tasa ajustada por riesgo.

Sin embargo, cuando se usa una tasa de actualización ajustada por riesgo es incorrecto referirse a un valor esperado del valor de la inversión 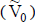y a la variabilidad de ese valor (el desvío estándar, 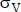), ambos determinados a partir de la distribución de probabilidad del flujo de fondos³⁴. Esta variabilidad del valor no se puede interpretar de modo claro, porque se ha determinado con una tasa de actualización que compensa la variabilidad del flujo de fondos. Por esto, considerar que esa variabilidad 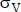es un elemento más en la interpretación del valor 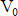que se calcula implicaría que se está teniendo en cuenta dos veces el riesgo (mediante la tasa ajustada por riesgo y al evaluar la inversión según la variabilidad del valor que se calcula con esa tasa).

A fin de que exista consistencia entre el riesgo medido como variabilidad del valor, y la cuantificación de éste, se plantea que la distribución del valor (con los parámetros 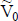y 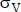) se calcule con la tasa sin riesgo. En este caso, el valor esperado en esa distribución 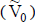no es una estimación del precio del flujo de fondos, sino que el valor realmente se obtiene después, con la evaluación del riesgo según la variabilidad 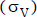³⁵. Esta es la característica del que se conoce como modelo de Hillier.

b) Origen y evolución de la medida de un valor probabilístico

La medida probabilística del valor se origina en el planteo que inicialmente realizó Frederick Hillier (Hillier, 1963), que se refería al cálculo del valor esperado y la variabilidad del valor reconociendo algunos tipos de dependencia serial de los importes periódicos.

En ese contexto, el valor como variable aleatoria (digamos, descripto con valor esperado y variabilidad, 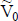y 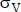) se obtendría usando una tasa de actualización que no contenga una compensación por el riesgo del flujo de fondos, es decir, una tasa sin riesgo, 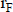(digamos, 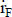si se expresa con una estimación puntual):

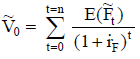Ecuación 5

Este valor esperado 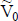se convierte en el valor estimado del flujo de fondos mediante un equivalente de certidumbre 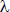, de modo que .

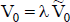El coeficiente 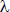refleja la preferencia por riesgo (según la variabilidad de la distribución del valor). Se denomina equivalente a certidumbre único (single certainty equivalent) para distinguirlo de los coeficientes de equivalencia a certidumbre de los importes periódicos con los que se puede expresar un flujo de fondos equivalente.

Estos coeficientes resultan de la estimación de la utilidad que se asigna a importes inciertos (específicamente, es el importe cierto que se considera equivalente a un importe sujeto a riesgo, como en una apuesta). Los coeficientes de equivalencia a certidumbre se usan para describir los resultados de las alternativas en la teoría formal de decisión.

Además, la relación entre la variabilidad del valor 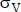(con tasa sin riesgo) y el coeficiente de equivalencia a certidumbre 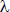que se usa para la valuación debería considerar el efecto de los riesgos diversificables. El desvío estándar del valor es un indicador de riesgo total (como lo es el desvío estándar de los importes periódicos), mientras que el valor que se busca calcular es un estimado del valor de mercado del flujo de fondos. Ese valor, entonces, reflejaría el rendimiento que compensa sólo el riesgo sistemático pertinente.

Este método de evaluación de proyectos basado en el valor probabilístico tuvo difusión académica durante los años 1960, y se podía encontrar mencionado también como enfoque de Hillier y Hertz, ya que podía aplicarse con las medidas de la distribución de probabilidad del valor formuladas inicialmente por Hillier, o bien con el cálculo de esa distribución mediante simulación aleatoria que planteó David Hertz (aunque él no lo aplicó a una distribución del valor actual, sino de la tasa interna de rentabilidad)³⁶.

El cálculo de un valor probabilístico de modo analítico (al estilo de Hillier, no con técnicas numéricas, como la simulación aleatoria) ha sido el objeto de varios modelos que procuran reflejar situaciones más complicadas de correlación entre los importes periódicos³⁷.

Estos modelos se plantean como base para el tipo de "análisis de riesgo de proyectos" que se comenta en el apartado a anterior, y no son claros en cuanto a la tasa de actualización que suponen (ya que se suele hacer una referencia genérica a la "tasa de actualización" o la "tasa de interés"). Puesto que no consideran el uso del factor de equivalencia 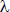, se infiere que el valor esperado que resulta es una estimación del precio, es decir, que se usaría una tasa ajustada por riesgo. Entonces, presentan el problema de interpretación de la variabilidad (que puede provocar, en la evaluación, una consideración duplicada de la exposición al riesgo).

7.2 La medida de un valor supuestamente borroso

La noción de un valor borroso, calculado a partir de las estimaciones borrosas del flujo de fondos y de la tasa de actualización, comparte con la noción de un valor probabilístico el problema de la interpretación.

Hay formulaciones de los números borrosos aplicados al cálculo de valor actual desde mediados de los años 1980. A partir de los años 1990 se presentan desarrollos generalizados, que se comentan en este apartado, para calcular un valor (más específicamente, un valor actual neto) borroso. Esos desarrollos analíticos parten de una estimación borrosa del flujo de fondos y de la tasa de actualización, y obtienen expresiones formales para calcular el valor borroso. En algunos casos, también se considera un estimado borroso de la inversión inicial³⁸ y de la vida económica de un proyecto.

a) Una formulación del denominado "valor borroso"

Chiu y Park (1994) realizan un planteo general para el cálculo del valor actual neto mediante la actualización de un flujo de fondos borroso. El resultado es un valor como un número borroso, con una función de pertenencia no lineal. Proponen un cálculo aproximado como una forma de simplificación operativa, suponiendo que el valor actual neto es un número borroso triangular.

De este modo, se calculan las cifras de valor para los intervalos de pertenencia extremos (α-corte 0, con el significado de esta noción que se explica en el apéndice 2), y el valor con las cifras de máxima posibilidad del flujo de fondos (α-corte 1). El valor se especifica como el número borroso:

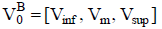Ecuación 6

Con la estimación de los componentes del flujo de fondos se obtienen los importes periódicos 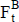como números borrosos. La tasa de actualización se estima como un número borroso 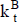. Se consideran los extremos de esos números borrosos (α = 0) y el importe de máxima posibilidad (α = 1).

En cada importe periódico, el intervalo de mínima posibilidad es 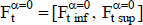, y el importe de máxima posibilidad es 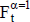. Se procede del mismo modo con la tasa de actualización: 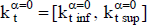y .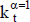

Se calcula el valor en los extremos y para la estimación de máxima posibilidad:

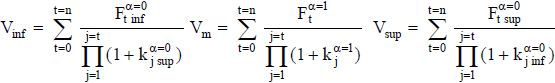Este cálculo es el que se comentó en el apartado 4.2, señalando que no es congruente con el uso de una tasa de actualización ajustada por riesgo. En el caso del proyecto EME (que se desarrolla en el apéndice 3) implica decir que el valor actual neto es un número borroso entre $ 224 negativo y $ 1.046 (figura 13).

Figura 13 Un ejemplo de VAN borroso correcto e incorrecto

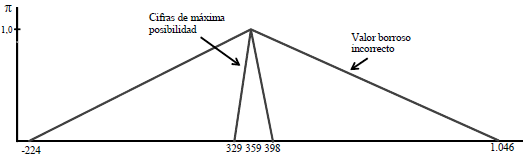
Al expresar la estimación de valor de ese modo no se tiene en cuenta que la imprecisión acerca del proyecto o el negocio (que se traduce en números borrosos con un rango mayor o menor) es parte de lo que se consideraría al estimar un adicional por riesgo en la tasa de actualización. Ese rango del flujo de fondos está compensado en la valuación, y no debe interpretarse como información acerca del riesgo del proyecto que se agrega a la compensación que está incluida en la tasa.

Por eso, en definitiva, los cálculos de valor con estimaciones borrosas del flujo de fondos se resumen en la cifra (o el intervalo) de máxima posibilidad. El resultado es similar a realizar la valuación con los importes desborrosificados, tal como se explicó en el apartado 4.2.

b) Estudios que se refieren a una medida de "valor borroso"

Los estudios de este tema son realizados, principalmente, por autores que provienen del ámbito de aplicación de las disciplinas matemáticas a las decisiones³⁹. Tal vez por esto no son suficientemente claros en la distinción del efecto que tiene, en la interpretación del valor calculado, el uso de una tasa de actualización ajustada por riesgo.

Algunos se refieren a la "tasa de actualización" (discount rate), y se podría llegar a inferir de las cifras en los ejemplos numéricos que están considerando una tasa ajustada por riesgo. En otros casos se menciona que la tasa es de costo de capital, por lo que parecen referirse a una tasa ajustada por riesgo. También se hace referencia a una "tasa de interés", y en un caso se dice: "tasa de interés borrosa para representar el costo de capital de la empresa".

La distinción, sin embargo, es fundamental para interpretar el valor que se calcula. Como se comentó para el valor probabilístico, la borrosidad del valor (originada en la borrosidad del flujo de fondos) es una medida relevante de incertidumbre sólo si los importes se actualizan con una tasa sin riesgo.

Con ese cálculo se obtiene un número borroso que representa una dimensión del valor, ya que no incluye explícitamente la compensación por el riesgo⁴⁰. El riesgo se expresaría con una medida del grado de "borrosidad" (análogo a la variabilidad de una distribución de probabilidad), y el valor del proyecto o el negocio se calcula considerando un corrector por borrosidad (análogo del coeficiente de equivalencia a certidumbre 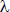que se comenta en el apartado 6.1 para la expresión probabilística).

Por el contrario, el cálculo produce directamente un estimado del valor cuando el riesgo (expresado con la borrosidad o la variabilidad del flujo de fondos) está compensado en la valuación mediante el adicional por riesgo en la tasa de actualización.

Similar aspecto debe considerarse en la versión borrosa del "análisis de riesgo". Kahraman y Kaya (2010) desarrollan el cálculo de la probabilidad borrosa de que el valor actual neto de un proyecto sea menor que cero.

Esta es una aplicación a la valuación de proyectos de inversión de la medida posibilística de la probabilidad (lo que se denomina "posibilidad de la probabilidad"). Se calculan probabilidades borrosas de determinadas características del proyecto a partir de estimaciones borrosas del flujo de fondos esperado y de su variabilidad (desvío estándar). Para esto, ellos usan una tasa de actualización ajustada por el riesgo del proyecto.

Sevastjanov, Dimova y Sevastianov (2006) consideran, entre los métodos para estimar el "riesgo financiero" de un proyecto, una evaluación de la borrosidad del valor borroso (fuzziness of the fuzzy value) según el rango de soporte del número (MNF, measure of non fuzziness).

Gutiérrez Betancur (2006) plantea una expresión del valor borroso mediante el cálculo de un intervalo en el nivel de máxima presunción (o posibilidad), y en los extremos inferior y superior. El número borroso del valor de máxima presunción puede entenderse como una medida desborrosificada del valor, ya que el intervalo en ese nivel refleja la borrosidad de los estimados del flujo de fondos y de la tasa de actualización de máxima presunción. Ese valor de máxima posibilidad puede interpretarse como un intervalo de valor con el sentido comentado en el apartado 5.3.

Como se ha insistido, un valor borroso con las características mencionadas (que reflejan la noción de que, como el flujo de fondos se estima con números borrosos, el valor es un número borroso) produce confusión en la interpretación.

Esta confusión en algunos casos es mayor al incorporar nociones probabilísticas en la borrosidad. Por ejemplo, Tsao (2005 y 2012) calcula un valor borroso con la "tasa de costo de capital" para cada escenario, y con esto determina un valor esperado borroso y una variabilidad borrosa (varianza y desvío estándar borrosos)⁴¹. Con ambos obtiene un coeficiente de variación, que a su vez desborrosifica con un método complicado (la media de las eliminaciones, mean of removals, método que reconoce mejor la amplitud de la borrosidad), y con este indicador se realiza la comparación de proyectos.

El asunto de la comparación entre alternativas tiene también sus variantes. La mayoría de los estudios comentados apuntan a calcular un valor actual neto como indicador para la selección de proyectos (podría decirse, un valor para la comparación de proyectos, y no una valuación). Dado que consideran expresiones borrosas de ese indicador, proponen formas de comparación que permitan el ordenamiento de los proyectos para las decisiones de inversión. Para ese ordenamiento se plantea: 1) alguna variante de desborrosificación del valor actual neto borroso, o 2) la aplicación de algún método para comparar y ordenar números borrosos⁴².

El primer caso, la desborrosificación del valor, puede verse como un camino más complicado para obtener, finalmente, un valor que tenderá a ser similar al que se calcula directamente con el flujo de fondos desborrosificado y la tasa ajustada por riesgo.

En el segundo caso hay que tener en cuenta que los métodos para comparar números borrosos son formalmente complicados, lo que dificulta la comunicación, y pueden dar diferentes ordenamientos⁴³. Además, con ellos no se obtiene una estimación del valor, sino sólo un orden de los valores borrosos. Es decir, un orden de los valores de las alternativas que, por lo comentado, están incorrectamente expresados como números borrosos.

8. Resumen: Imprecisión de las estimaciones, imprecisión de los conceptos

La incertidumbre se suele considerar en la valuación de proyectos o negocios mediante una tasa de actualización ajustada por riesgo. Esta tasa permite valuar con el flujo de fondos, y éste puede estimarse de modo puntual, explícitamente probabilístico o borroso.

La diferencia entre la estimación puntual y las otras dos es la cantidad de información que se transmite acerca del flujo de fondos. La diferencia entre la estimación probabilística y la estimación borrosa es el modo en que se expresan las medidas y, específicamente, el modo de interpretar la imprecisión de las estimaciones.

Por el tradicional desarrollo de la teoría de probabilidad, en las evaluaciones económicas la forma más difundida es la expresión de las estimaciones con distribuciones de probabilidad. Al expandirse la modalidad de descripciones borrosas (y la consiguiente teoría de posibilidad) se ha planteado que la expresión posibilística es más adecuada para el tratamiento de la imprecisión de las medidas.

La imprecisión, sin embargo, puede ser tratada también adecuadamente con el marco de la probabilidad imprecisa. Se argumenta que, para tratar la imprecisión, el marco de la posibilidad tiene ventajas sobre el marco de la probabilidad. Este argumento se basa en una asociación de la probabilidad con la incertidumbre aleatoria y de la posibilidad con la incertidumbre epistémica (que equivale a la distinción de riesgo e incertidumbre de Knight).

Pero esta asociación no es tan nítida como se plantea. Ambos campos se han desarrollado en los últimos años para una mejor descripción en las situaciones de incertidumbre (de diverso origen). Para usar una terminología que se ha difundido con la lógica borrosa (que se relaciona la teoría de posibilidad), habría que reconocer que esa distinción no es crisp sino fuzzy.

Probabilidad y posibilidad son marcos de descripción bastante próximos, por la noción de probabilidad subjetiva como grados de creencia. Los gráficos de creencia (en posibilidad) y las distribuciones subjetivas (en probabilidad) son expresiones de algún modo coincidentes: el uso práctico de las distribuciones de probabilidad las acerca a las funciones de posibilidad.

De igual manera, se puede considerar que el tratamiento probabilístico mediante simulación, cuando hay poca información observable para basar las estimaciones, no difiere mucho de la estimación con intervalos simples.

Posiblemente la expresión borrosa y posibilística es un lenguaje adecuado para muchas estimaciones técnicas y económicas, ya que evoca directamente la medida que se hace a partir de un conocimiento incompleto. En ese sentido, puede ser la base de las estimaciones para la valuación de proyectos.

Pero las diferencias no son tan significativas cuando se llega al nivel del modelo financiero del negocio en el que se basa la valuación. Tal vez por eso el lenguaje de la posibilidad y los números borrosos no se ha difundido tanto en el ámbito de valuación como ha ocurrido en otros, y sigue siendo un tema de alcance más bien académico.

A esto puede contribuir la orientación que se da al tema: se presenta el "valor borroso" como resultado de un cálculo diferente, con expresiones formales muy específicas (y a veces complicadas).

En este ensayo se ha presentado algo que es exactamente opuesto: para la valuación no existen diferencias en la formulación, sino sólo en la forma en que se llega a la estimación del flujo de fondos. Se ha insistido en que la noción de "valor borroso" (como la de "valor probabilístico") contiene una confusión básica, al no reconocer que la incertidumbre del flujo de fondos está compensada en la tasa de actualización ajustada por riesgo.

También se han considerado las características de un valor borroso auténtico, que puede determinarse con estimaciones probabilísticas o borrosas. Este valor transmite explícitamente, cuando se considera necesario, el grado de imprecisión de las estimaciones que se ve como irreductible en un análisis razonablemente informado.

Se puede decir, entonces, que tanto las estimaciones probabilísticas como las borrosas son modos adecuados de manejar la imprecisión de las estimaciones para la valuación. Y también que las nociones que se presentan de un "valor probabilístico" y un "valor borroso" son imprecisas de un modo muy distinto: no se refieren a la imprecisión de las estimaciones, sino que manifiestan imprecisión en los conceptos para la valuación.

Apéndice 1: La valuación y los títulos que son efectiva o potencialmente transables

El valor de un proyecto o un negocio que genera un flujo de fondos 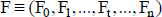, si el derecho a obtener estos importes puede transarse en el mercado financiero, es la suma 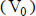del precio, en el momento de la valuación, de los títulos equivalentes.

Esta definición es ampliamente usada porque permite determinar las condiciones en que el valor es independiente de las preferencias por consumo del decididor. Es decir, es un valor común para todos los que compartan la expectativa acerca de F, y no está influido por los perfiles de consumo deseados por cada individuo.

El enunciado se conoce como el teorema de separación de Fisher⁴⁴, referido al valor de las inversiones en activos que es reconocido por inversores con diferentes preferencias temporales por consumo.

a) Si existe certeza acerca de los importes periódicos F que se consideran para el negocio, y en la fecha de valuación (digamos, hoy) se pueden transar promesas de pago para cada importe, el valor de ese flujo de fondos es la suma de los precios de esos títulos.

Consideremos que 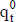es el precio hoy de un título sin riesgo que paga 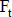al fin del período t, y nada antes o después; es lo que se conoce como un bono cupón cero con vencimiento en t. Este precio puede escribirse como un valor actual, con la tasa sin riesgo :

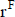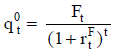En esta expresión, 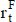es la tasa equivalente anual vigente en el momento de la valuación de un pago único dentro de t años.

El valor del negocio que genera el flujo de fondos F es la suma del valor que tienen esos títulos equivalentes:

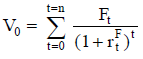Ecuación 1.1

La tasa de actualización puede considerarse como la equivalente anual de las tasas anuales acumuladas de los períodos anteriores a t, ya que reflejaría la estructura temporal de tasas que existe en el momento de la valuación:

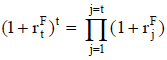b) En condiciones de incertidumbre los importes futuros F no se conocen. Consideremos que en tal situación se pueden enumerar los posibles estados que afectan al negocio.

"Estado" se refiere a la descripción completa de un escenario relevante para el negocio o la inversión: en el momento t sólo se materializa uno de los estados 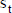. El importe periódico del flujo de fondos se estima para cada estado 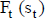de cada período t: es un flujo contingente a estados.

Si el mercado de títulos es completo, existe un precio para el título que paga un peso (una unidad monetaria) sólo si ocurre cada estado. Estos son títulos puros (o primitivos), cuyos precios son independientes entre sí⁴⁵. El valor hoy del título puro, 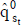, es el precio de un peso contingente al estado 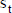. Es el valor actual de un peso con certidumbre en el período t, si y sólo si se materializa el estado .

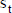Los importes del flujo de fondos condicionales a cada estado, 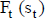, se valúan con los precios 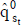en los 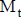estados 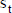en cada período:

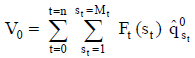Ecuación 1.2

El valor no depende de la preferencia temporal por consumo ni de la confianza que una persona tenga en la materialización de cada estado. Se pueden considerar, por ejemplo, dos personas con diferentes creencias acerca de la materialización de un escenario en cada período (digamos, una piensa que los escenarios serán los más favorables, y la otra piensa que los escenarios serán medios o desfavorables). Ambas coincidirán en que el valor del negocio es el mismo, . La condición de esto es que tengan similar expectativa acerca del importe F en cada escenario (que coincidan en cuáles son los títulos puros equivalentes) y que existan títulos puros para cada contingencia (que el mercado sea completo).

Esta forma de considerar el valor se denomina enfoque de preferencia tiempo-estado (time-state preference), y es una generalización del teorema de separación de Fisher para las situaciones con incertidumbre; por esto, esa proposición también suele denominarse separación de Fisher-Hirshleifer⁴⁶.

En estas condiciones, no es necesario considerar la posibilidad de cada estado (probabilidad de escenario), ya que está contenida en el precio de los títulos puros correspondientes. Sin embargo, para algunos fines se escribe la ecuación 1.2 con precios normalizados de estos títulos puros.

Para tal expresión se considera el valor unitario de un bono sin riesgo cupón cero con vencimiento en cada período. Estos bonos pagan un peso en el período t, con independencia del estado que se materialice; por tanto, su precio hoy debe ser igual a un conjunto de títulos puros para el período t:

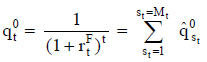Los precios hoy de los títulos puros se pueden expresar en el período t: 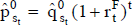. La magnitud 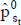es una normalización de esos precios, que se interpreta como una probabilidad neutral al riesgo: tiene la propiedad de una probabilidad (la suma para todos los estados de cada período es igual a 1), y refleja la probabilidad que se asigna a cada estado en condiciones de indiferencia frente al riesgo (ya que se relaciona con el título puro que corresponde a cada estado, en un mercado financiero en que se cubren todos los estados).

Sustituyendo en la ecuación 1.2 se obtiene una expresión del valor a partir del flujo de fondos esperado en cada período:

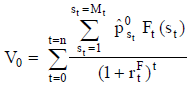Ecuación 1.3

El flujo de fondos esperado se calcula con la probabilidad neutral al riesgo de cada estado 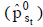; ésta refleja la variabilidad de los estados tal como es evaluada en el mercado.

El numerador en la ecuación 1.3 es una expresión del flujo de fondos equivalente a certidumbre, según la perspectiva reflejada en los precios de los títulos puros. No es un equivalente a certidumbre para un decididor (que puede ser distinto del importe equivalente a certidumbre para otro), sino que refleja la perspectiva intersubjetiva del mercado.

En los mercados no suelen transarse títulos puros como los mencionados, ya que lo más frecuente es que los títulos paguen importes en varios estados. Sin embargo, esto no implica que los mercados no puedan ser completos: es suficiente que los títulos puros puedan replicarse mediante carteras de títulos existentes⁴⁷.

c) Consideremos que no está disponible un título puro para cada estado en cada período, y que tampoco se puede replicar cada título puro con títulos existentes. Pero pensemos que sí se puede transar un título o cartera para el conjunto de resultados en cada período (los importes 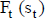que se generan en los estados del período t). Ese título tiene un precio 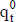, y entonces el valor es la suma de los precios de los títulos con los que puede transarse ahora los importes que se generarían en cada período.

En un contexto en el que las expectativas son homogéneas y los inversores son adversos al riesgo se verificaría la condición del modelo de valoración de títulos (capital asset pricing model, CAPM) sobre los rendimientos de esos títulos para los importes de cada período.

Si el importe esperado del período t está en función de los importes estimados para cada estado, y la tasa sin riesgo 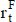y la tasa de rendimiento del mercado de títulos 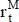se expresan como equivalentes anuales, el rendimiento esperado del título con precio 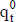es:

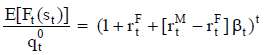En esta expresión, 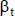es una medida estandarizada del riesgo sistemático de la cartera de títulos que equivale al conjunto de importes en el período t.

Por esto, el precio de esa réplica se puede expresar en función del importe esperado y la tasa que compensa el riesgo sistemático:

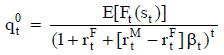El valor del negocio es la suma de los precios 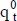de todos esos títulos o carteras:

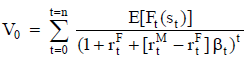Ecuación 1.4

Sin embargo, si hay títulos cuyo flujo de fondos es equivalente al del negocio, y sus precios son conocidos, no es necesario este cálculo, ya que basta con sumar esos precios para obtener el valor del negocio. La ecuación 1.4 es sólo una expresión formal que muestra el contenido analítico de esa suma.

La ecuación 1.4 puede expresarse en forma condensada con una tasa ajustada por riesgo 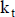, como tasa anual equivalente para el período t:

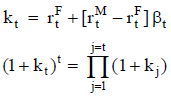Y entonces

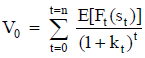Ecuación 1.5

Por el contrario, si no hay títulos que permitan esa réplica directa, es necesario estimar cuáles serían, hipotéticamente, los precios de esos títulos, si existieran. Esto se hace con la ecuación 1.4 (o 1.5), que está expresada con una tasa de actualización ajustada por riesgo según CAPM. O bien con la ecuación 1.3, que está expresada con un flujo de fondos equivalente a certidumbre según probabilidades de mercado (no la probabilidad real de cada estado), es decir, con un flujo de fondos ajustado por riesgo⁴⁸.

En tal situación, el teorema de separación de Fisher-Hirshleifer no es el fundamento del valor que se calcula: no puede considerarse que el valor es, necesariamente, independiente de las preferencias temporales por consumo y actitud frente al riesgo de cada decididor.

Esto significa que la valuación de un flujo de fondos (que se mide de modo que muestre razonablemente el posible desempeño del negocio) es una estimación del precio que podrían tener esos títulos equivalentes, si se transaran. Y sólo en este sentido se dice que la valuación no es, necesariamente, la determinación de una medida de valor que es válida para las decisiones de todos los inversores (aunque trata de aproximar un número que lo sea).

d) El ajuste por riesgo del flujo de fondos o de la tasa de actualización. La ecuación 1.3 es una expresión del ajuste por riesgo del flujo de fondos realizado con probabilidades de mercado.

La especificación del flujo de fondos ajustado por riesgo se origina en la noción de un importe equivalente a certidumbre, que se introduce en la economía y en la teoría formal de decisión en los años 1940. A principios de los años 1950, tanto Kenneth Arrow como Friedrich y Vera Lutz se refieren a los equivalentes a certidumbre para considerar las decisiones en condiciones de riesgo.

En ese contexto se considera que los importes equivalentes a certidumbre se miden según la función de utilidad, que refleja la actitud frente al riesgo del destinatario de la valuación. Se sustituye el flujo de fondos 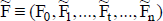por un flujo de importes equivalentes a certidumbre, 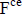, que se actualiza con la tasa sin riesgo.

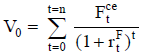Entonces, 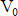es el valor para ese decididor, y no el precio de mercado del flujo de fondos.

El importe equivalente a certidumbre se suele expresar con un coeficiente de equivalencia a certidumbre, 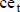, de modo que .

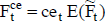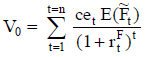Ecuación 1.6

La valuación en condiciones de mercado puede interpretarse que refleja una probabilidad ajustada de los estados o escenarios (Myers, 1968; Samuelson y Merton, 1969). Este "ajuste", cuando hay aversión al riesgo, implica un aumento de la probabilidad de los resultados desfavorables y una disminución de la probabilidad de los favorables, y esto es lo que después se conoce como valuación con probabilidades neutrales al riesgo.

Si el flujo de fondos esperado se actualiza con una tasa que representa el rendimiento de los títulos según los precios en condiciones de equilibrio del mercado de capital, el valor que se mide es también el precio de mercado del flujo de fondos incierto. Se dice que la valuación se realiza con una tasa ajustada por riesgo.

La precisión de esa estimación del precio depende de cómo se estimen los componentes CAPM: el adicional por riesgo del mercado y la covariabilidad de los importes periódicos con el rendimiento del mercado de títulos (coeficiente 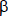con el mercado) (Myers y Turnbull, 1977).

La consistencia entre las formulaciones según las ecuaciones 1.5 (tasa ajustada por riesgo) y 1.6 (flujo de fondos ajustado por riesgo) requiere que el impacto de la incertidumbre que se considera en la valuación tenga una forma temporal específica. En una situación multiperiódica no pueden existir, simultáneamente, una tasa ajustada por riesgo constante, 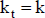, una tasa de interés sin riesgo constante, 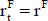, y un coeficiente de equivalencia constante, 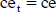(Robichek y Myers, 1965). Las magnitudes de mercado (sean probabilidades o rendimientos) deberían reflejar esa congruencia.

Apéndice 2: Números borrosos y operaciones aritméticas

a) Los números borrosos más usuales

Se define que un número borroso es un subconjunto de los números reales con una función de pertenencia (o membresía, membership function) que es una imagen (mapeo) continuo de la línea real en el intervalo [0,1]. Esa función se puede considerar una función de posibilidad: la máxima posibilidad es 1 (que no equivale a certidumbre, como es el caso en una expresión probabilística).

Un número borroso puede tener distintas formas, según las características de la imprecisión que refleja, y la función de pertenencia puede ser lineal o no lineal. Las funciones lineales triangular y trapecial son fáciles de interpretar, y por eso son las de uso más difundido en las estimaciones económicas y de negocios.

Un número borroso triangular (que se suele abreviar NBT, o TFN, triangular fuzzy number) se especifica como [a, m, b], donde a y b son los límites inferior y superior, y m es el valor de máxima posibilidad (o presunción). La función de pertenencia es cero para cualquier número fuera de los extremos a y b, y es creciente entre a y m y decreciente entre m y d. Es decir, a < m < b. Por ejemplo, la tasa de actualización se estima entre 9% y 11%, y la que se considera más posible es 10%.

Formalmente, la función de pertenencia de un número borroso triangular A es:

En la figura 2.1 se muestran números borrosos triangulares; el eje horizontal es la magnitud de la variable, y el eje vertical es la posibilidad o presunción (entre 0 y 1).

Figura 2.1 Números borrosos triangulares

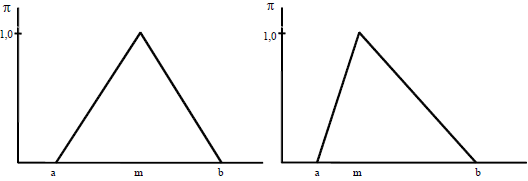
Un número borroso trapecial (que se suele abreviar NBTp, o TpFN) se especifica como [a, m, n, b], con a < m = n < b; a y b son los límites inferior y superior, y los valores de máxima posibilidad están en el intervalo m, n. La función de pertenencia de un número trapecial B se especifica como proporcional creciente entre a y m, y proporcional decreciente entre n y b:

La figura 2.2 muestra representaciones de números borrosos trapeciales.

Figura 2.2 Números borrosos trapeciales

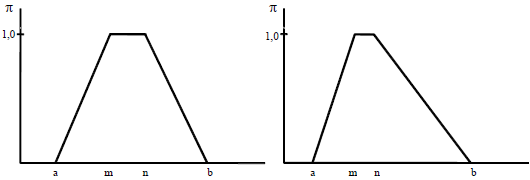
Un intervalo simple es [a, b] y un número preciso es [a]. Las estimaciones, entonces, se pueden expresar con un número preciso, un intervalo de confianza, una tripleta de confianza o un cuádruplo de confianza.

Hay formas lineales con cinco parámetros [a, c, m, d, b] que, si es el caso, permiten una mejor especificación de las variables. La figura 2.3 muestra dos configuraciones, y su comparación con un número borroso triangular.

Figura 2.3 Números borrosos con cinco parámetros

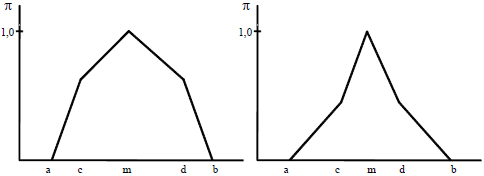
b) Los intervalos α-cortes

Un número borroso se describe mediante intervalos con los denominados α-cortes (α-cuts), que son intervalos simples con posibilidad de ocurrencia α. La posibilidad se expresa entre 0 y 1, y entonces el intervalo con posibilidad 0,5 será más amplio que el intervalo con posibilidad 0,75 y más estrecho que el intervalo con posibilidad 0,25.

Un α-corte de un número borroso A se designa como 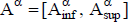. También se suele usar la notación 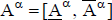. La figura 2.4 muestra α-cortes de un número triangular. Un número borroso, entonces, se puede ver como un conjunto de intervalos anidados.

Figura 2.4 Ejemplo de α-cortes de un número borroso triangular

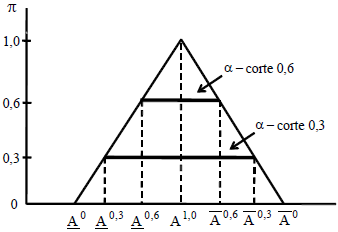
Si A es un número borroso triangular NBT [a, m, b], el intervalo se calcula:

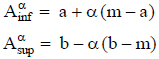Al comparar las formas de cinco parámetros con la forma triangular, se observa que las diferencias están en la "cintura" de cada función: de adentro hacia afuera, es algo parecido a la figura corporal a los 15 años, a los 25 años y a los 40 años.

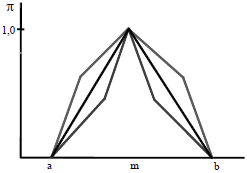Por ejemplo, el volumen de ventas se estima [300, 450, 550]. Los intervalos para los cortes de posibilidad son [300 + 150α, 550 - 100α]. Para α = 0,5, el intervalo es [375, 500].

Los extremos del intervalo del α-corte de un número borroso trapecial NBTp [a, m, n, b] se calculan considerando los valores m y n del intervalo de máxima posibilidad:

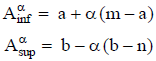Los α-cortes se pueden considerar como escalas semánticas con una determinada cantidad de niveles. Por ejemplo, de tres niveles (ternaria), de cinco niveles (pentaria), de once niveles (endecadaria), que se detallan en el cuadro 2.1.

Cuadro 2.1 Algunas escalas semánticas

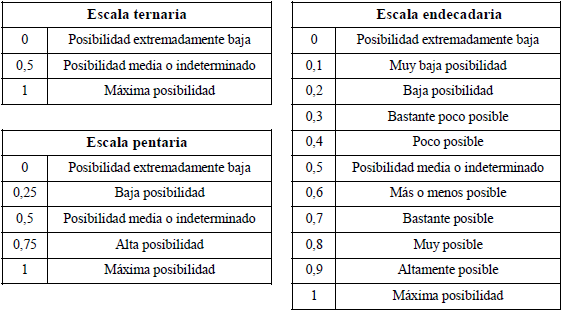
El extremo inferior (0) puede verse como imposible (en lógica, la proposición es falsa). Sin embargo, en las estimaciones de posibilidad representa la creencia de que es un valor "prácticamente imposible", aunque tiene algo de posibilidad (y por eso se lo considera): implica decir que es estrictamente imposible un valor menor que ése.

Lo mismo se considera con el extremo superior (1): es la máxima posibilidad (en lógica, la proposición es verdadera), pero no implica certidumbre sino máxima confianza de que ése es el valor que se observará. El punto medio, 0,5, es de indeterminación (en lógica, equivale a decir "ni verdadero ni falso").

Cuando se usan números borrosos triangulares o trapeciales, las escalas de tres o cinco niveles son suficientes para reflejar el comportamiento en los intervalos con α-cortes: por ejemplo, α = 0, α = 0,5, α = 1.

Si se estiman números borrosos con más parámetros, o no lineales, o bien el número borroso resultante de operaciones puede tener una figura que no es definidamente triangular o trapecial, es conveniente que la descripción con α-cortes se haga con una escala endecadaria. Por esto, una de las desventajas de la aritmética borrosa es que los α-cortes significativos puede que no sean los mismos en todas las variables.

c) Operaciones con α-cortes

Las operaciones con números borrosos (suma, sustracción, multiplicación, división, inversa y cambio de signo) se pueden realizar con α-cortes, aplicando la aritmética de intervalos. Es una forma sencilla de operar con números borrosos.

Si se tienen dos números borrosos positivos (el extremo inferior es mayor que cero), A y B, las operaciones con los α-cortes 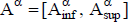y 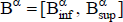son las que se detallan en el cuadro 2.2.

Cuadro 2.2 Operaciones con α-cortes

Una característica de las operaciones con intervalos es que la multiplicación y la división no son distributivas. Por esto, para obtener un resultado que es una función de varias variables estimadas debe formarse un modelo de cálculo en el que no se aplique esa propiedad (es decir, formular un modelo en el que cada variable intervenga sólo una vez). De lo contrario, la amplitud del intervalo aumenta, ya que se "agrega" incertidumbre cada vez que se considera la variable (por el supuesto de correlación completa que existe en el cálculo con intervalos).

Las operaciones se pueden realizar también con un calculador de intervalos con los α-cortes (como Interval Solver), y así se forman los números borrosos que sea de interés comunicar. Cuando hay varios posibles intervalos según sea el modo en que se especifica el modelo, el calculador considera que la mejor medición es el intervalo más pequeño; esto se denomina optimización de los cálculos con intervalos, y su uso es recomendable en los modelos complejos, con funciones que relacionan unas variables con otras.

d) Ejemplo de operaciones con intervalos

Consideremos un ejemplo de medición de la ganancia operativa. Las estimaciones para el primer año se muestran en el cuadro 2.3, panel A, expresadas como números borrosos triangulares (precio de venta, costo variable unitario, tasa efectiva de impuesto a las ganancias y tasa de inflación) y trapeciales (volumen de ventas y costos fijos). Las cifras monetarias se estiman en moneda corriente de ese año.

Cuadro 2.3 Estimaciones para la proyección de la ganancia borrosa

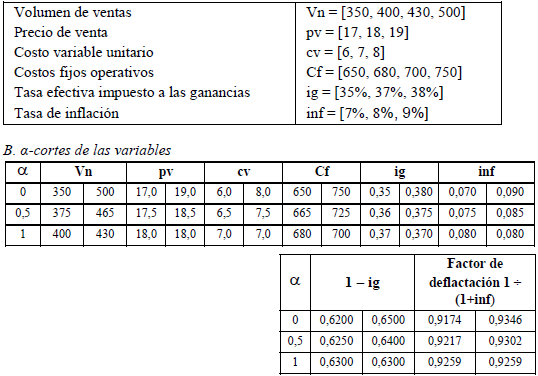
En el panel B se muestra el detalle de los intervalos de las variables para las operaciones (α-cortes en 0, 0,5 y 1).

Para calcular la ganancia en moneda inicial se aplica la siguiente ecuación:

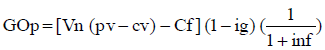El resultado se muestra en el cuadro 2.4 y la figura 2.5. La ganancia operativa estimada es un número borroso trapecial: GOp = [1.365, 2.158, 2.363, 3.554].

Cuadro 2.4 Estimación correcta de la ganancia borrosa

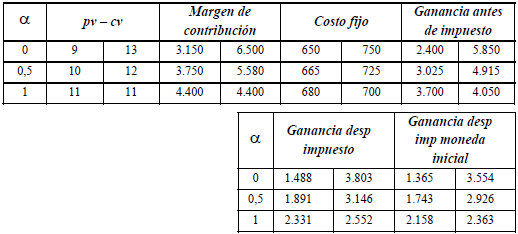
Figura 2.5 Ejemplo: Ganancia estimada

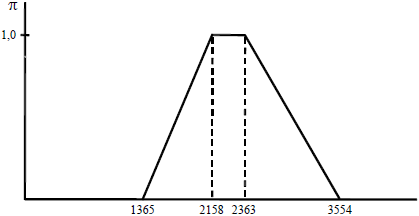
Con fines comparativos, en el cuadro 2.5 se muestra el resultado si la ganancia en moneda inicial se calcula con un modelo que distribuye una multiplicación:

Cuadro 2.5 Una estimación incorrecta de la ganancia borrosa

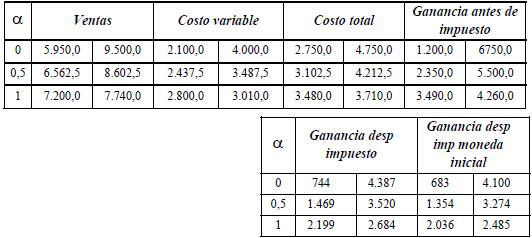
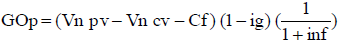El resultado es que la ganancia operativa en moneda inicial es un número borroso trapecial con un rango mucho mayor que el determinado antes: GOp = [683, 2.036, 2.485, 4.100]. Y también es más amplio el intervalo de máxima posibilidad: 2.036, 2.485, frente a 2.158, 2363.

Y se obtiene otro intervalo si la ganancia se calcula:

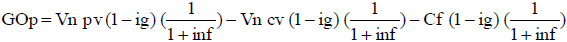Al realizar más distribuciones de la multiplicación, el intervalo es aún más amplio, GOp = [499, 2.036, 2.485, 4.207], como se observa en la figura 2.6.

Figura 2.6 Ejemplo: Ganancia estimada, medidas incorrectas

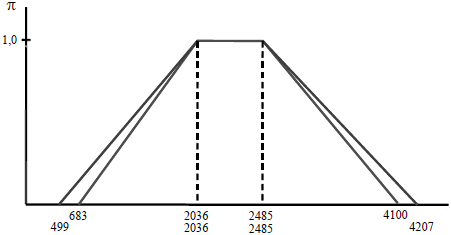
Estas son estimaciones incorrectas de la magnitud (en este caso, la ganancia) porque se realizan considerando varias veces el intervalo de una o más variables. En términos borrosos, tal forma de operar agrega borrosidad a la magnitud resultante: ésta se determina con una borrosidad mayor que la que surge de la borrosidad de las variables.

Apéndice 3: Ejemplos de cálculo de valor con números borrosos

Ejemplo EME

Se considera que las estimaciones de los componentes del flujo de fondos del proyecto EME finalmente se expresan como números borrosos triangulares [a, m, b] (cuadro 3.1).

Cuadro 3.1 Flujo de fondos

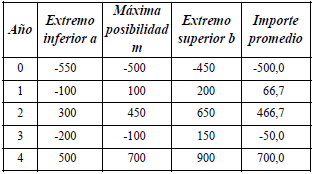
La tasa de actualización ajustada por riesgo de cada período se estima como números borrosos triangulares (cuadro 3.2).

Cuadro 3.2 Tasa de actualización

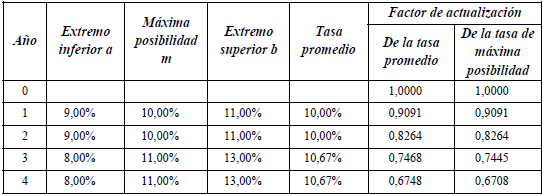
En la figura 3.1 se muestran gráficamente las estimaciones del flujo de fondos y la tasa de actualización.

Figura 3.1 Estimaciones Proyecto EME

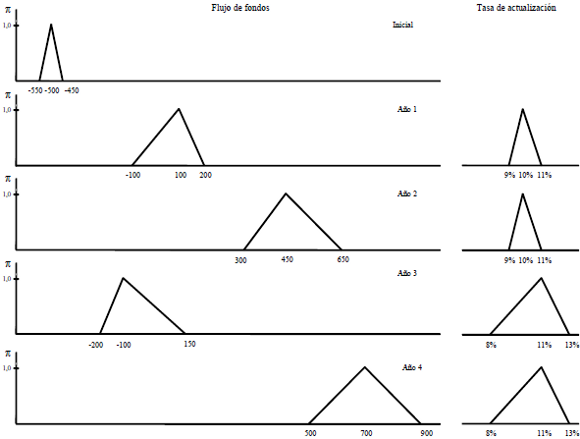
Se puede hacer una estimación puntual del valor actual neto de este proyecto:

1. Con el importe periódico desborrosificado según el promedio de los parámetros y la tasa de actualización también desborrosificada con el promedio:
2. Con la cifra de máxima posibilidad del importe periódico y la tasa de actualización de máxima posibilidad
3. En el cuadro 3.3 se muestran los resultados con las dos alternativas de desborrosificación.

Cuadro 3.3 Valor con flujo y tasa desborrosificados

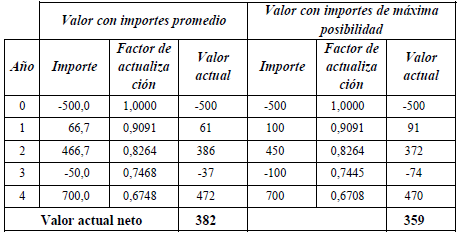
La diferencia que se observa entre las cifras de valor según una u otra forma de desborrosificación se origina en la asimetría de los números borrosos de los importes periódicos y de la tasa de actualización.

También se puede medir el valor en el rango determinado por la tasa de actualización, y el flujo de fondos desborrosificado:

1. Con el importe periódico promedio
2. Con el importe periódico de máxima posibilidad

Esta es una medida de valor auténticamente borroso, que se origina en la imprecisión en la estimación de la tasa de actualización.

El factor de actualización borroso, considerando los números borrosos de la tasa de actualización en cada período, se muestra en el cuadro 3.4.

Cuadro 3.4 Factor de actualización borroso

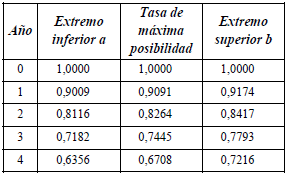
Cabe mencionar que la actualización es una división; como se explica en el apéndice 2, la división (o la inversa, que es el caso del factor de actualización) se hace cambiando los extremos del número. De este modo, los parámetros del número borroso resultante quedan ordenados en forma creciente.

En el cuadro 3.5 se muestra el valor determinado con las dos alternativas de desborrosificación del flujo de fondos que se consideran.

Cuadro 3.5 Valor borroso "auténtico"

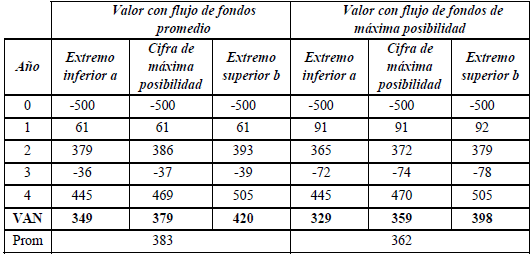
El cálculo se realiza con los extremos de la tasa de actualización (equivale a considerar corte con α = 0) y las cifras de máxima posibilidad con el corte α = 1 de la tasa (se obtiene la misma cifra que en el cálculo de un valor puntual).

Se puede decir que, con la estimación del flujo de fondos de máxima posibilidad, el valor actual neto está entre $ 329 y $ 398, y la cifra de máxima posibilidad es $ 359.

El valor es un número borroso triangular porque la tasa de actualización se estima de esa forma. El promedio de los parámetros de estos números borrosos se aproxima con el valor que se calcula con las cifras desborrosificadas de las tasas (con el promedio o la tasa de máxima posibilidad), según el cuadro 3.3: $ 383 frente a $ 382 con el promedio de los importes periódicos, y $ 362 frente a $ 359 con los importes de máxima posibilidad.

En una situación diferente, si la tasa se estimara en un intervalo simple (a, b), el valor sería también un intervalo simple (que se interpreta como el de máxima posibilidad).

En la figura 3.2 se muestran las dos estimaciones del valor actual neto borroso del proyecto EME.

Figura 3.2 Valor actual neto borroso Proyecto EME

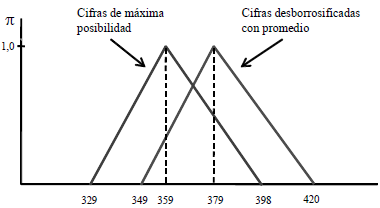
Finalmente, una aplicación incorrecta de la valuación con una tasa ajustada por riesgo con estimaciones borrosas informaría un rango de valor considerando toda la amplitud de la estimación de las cifras periódicas.

Con los números triangulares de los importes periódicos (cuadro 3.1) y de la tasa de actualización (cuadro 3.2) se calcula el valor actual neto como un número borroso con extremo inferior negativo en $ 224 y un extremo superior de $ 1.046 (cuadro 3.6). También en este caso, los parámetros de ese número borroso se obtienen calculando los extremos (α = 0) y el modo (α = 1).

Cuadro 3.6 Valor borroso incorrecto

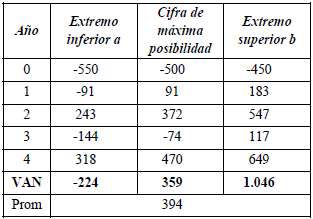
En estos resultados se observa plenamente el efecto del supuesto de correlación completa que tienen los cálculos con intervalos: los extremos se forman con las estimaciones "peores" y "mejores". En el extremo inferior, la mayor inversión y los menores importes positivos, y la tasa más alta; en el extremo superior, la menor inversión y los mayores importes positivos, y la tasa más baja.

Una observación operativa: dado que las cifras del flujo de fondos pueden ser positivas o negativas, en la estimación que se muestra en el cuadro 3.1 los parámetros están ordenados con su signo de modo estrictamente creciente. Así se opera como si fueran sumas (en el apéndice 2 se explica que la resta en los cálculos con intervalos se hace cambiando los extremos cuando el número que se resta está expresado con magnitudes positivas, ordenadas también de modo creciente).

En la figura 3.3 se muestran los valores borrosos calculados: las cifras correctamente borrosas (3.5) y las incorrectas (cuadro 3.6). Es claro que el rango de estimación del valor con el cálculo incorrecto tiene poco significado, teniendo en cuenta que la amplitud de los posibles resultados del proyecto en cada año se compensa, en la valuación, con el adicional por riesgo en la tasa de actualización.

Figura 3.3 Valor borroso correcto e incorrecto Proyecto EME

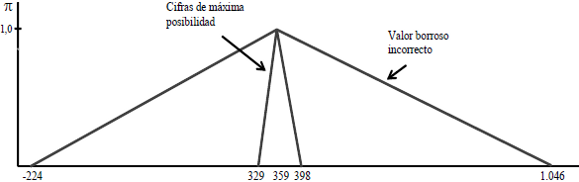
Ejemplo ENE

Se considera que las estimaciones de los componentes del flujo de fondos del proyecto ENE se expresan finalmente como números borrosos trapeciales [a, m, n, b] (cuadro 3.7).

Cuadro 3.7 Flujo de fondos

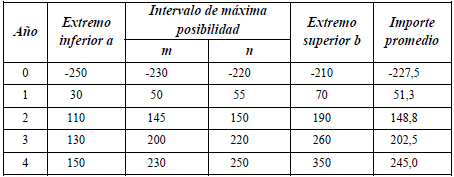
Se estima la tasa de actualización ajustada por riesgo de cada período igual que la planteada para el proyecto EME (cuadro 3.2).

El valor se calcula con importes desborrosificados, con las alternativas comentadas en el ejemplo EME. Los resultados se muestran en el cuadro 3.8.

Cuadro 3.8 Valor con flujo y tasa desborrosificados

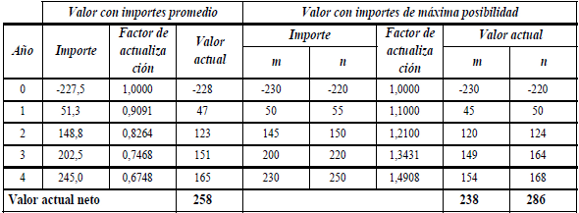
La medida con el importe promedio, $ 258, se interpreta de modo similar al cálculo con números triangulares. La medida con los importes del intervalo de máxima posibilidad de los números trapeciales es también un intervalo (el valor es entre $ 238 y $ 286). A menos que los números sean muy fuertemente asimétricos, este intervalo comprende al valor con importes promedio.

El valor se puede medir con el rango determinado por la tasa de actualización, considerando el flujo de fondos desborrosificado (con el importe periódico promedio), o bien con los importes de máxima posibilidad. Se usa el factor de actualización borroso que se muestra en el cuadro 3.4.

En el cuadro 3.9 se observa que el valor con el flujo de fondos promedio (cuadro 3.7, última columna) es un número borroso triangular ($ 240, $ 257, $ 279), ya que esta forma proviene de la tasa de actualización estimada con números triangulares.

Cuadro 3.9 Valor borroso "auténtico"

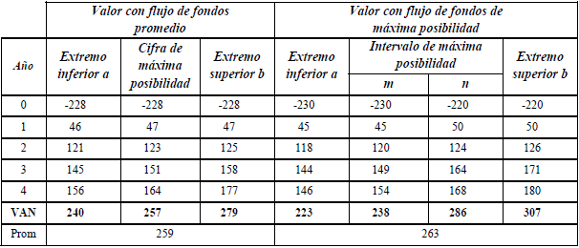
El valor con el intervalo de máxima posibilidad (m, n) de los importes periódicos (cuadro 3.7) es un número trapecial, que resulta de la forma triangular del factor de actualización.

El intervalo de máxima posibilidad del valor ($ 238, $ 286) se calcula con el intervalo de máxima posibilidad del flujo de fondos y la tasa de máxima posibilidad (equivale al corte α = 1). Los extremos ($ 223, $ 307) se calculan con el intervalo de máxima posibilidad de los importes y los extremos del factor de actualización (corte α = 0).

La figura 3.4 muestra las dos estimaciones del valor actual neto borroso del proyecto ENE.

Figura 3.4 Valor actual neto borroso Proyecto ENE

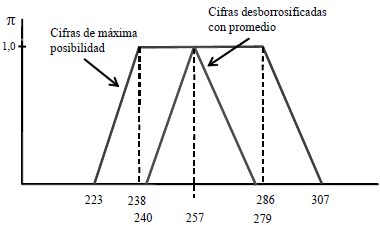
Con una finalidad puramente comparativa se puede hacer el cálculo incorrecto con los números borrosos completos del flujo de fondos (cuadro 3.7). Los resultados se muestran en el cuadro 3.10.

Cuadro 3.10 Valor borroso incorrecto

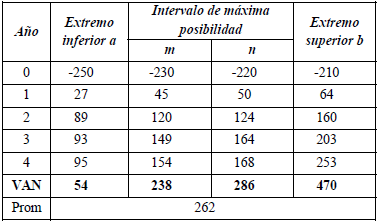
Es claro que el intervalo de máxima posibilidad es el mismo que en el cálculo anterior. Lo que cambia es la amplitud del rango de valor: implica decir que el valor puede estar entre $ 54 y $ 470, aclarando que éstos son extremos de baja posibilidad. El promedio, $ 262, es similar a los que se calculan con las variantes correctas (cuadro 3.9).

En la figura 3.5 se comparan los dos cálculos del valor actual neto borroso: la estimación correcta (cuadro 3.9) y la medida incorrecta (cuadro 3.10).

Figura 3.5 Valor borroso correcto e incorrecto Proyecto ENE

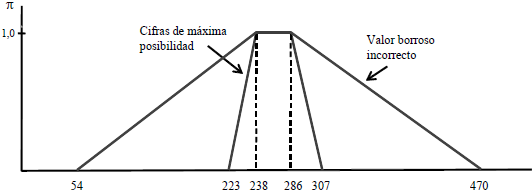
Notas
^• Presentado en las XXXII Jornadas Nacionales de Administración Financiera, SADAF, Valle Hermoso (Córdoba, Argentina), septiembre/2012.
¹ La posibilidad de replicar el proyecto o el negocio con títulos supone un mercado de capital completo, y por eso se dice que es el valor del negocio o el proyecto que tendría si estuviera representado en un título transado. Si bien es aplicable en muchas estimaciones, esta condición no se cumple cuando, como comentan Smith y Nau, "la introducción del proyecto en el mercado puede crear nuevas oportunidades de inversión financiera, y cambiar los precios de los títulos transados" (Smith y Nau, 1995: 805).
² En un proyecto existe, típicamente, un lapso de inversión (que se extiende en uno o más períodos del horizonte considerado) y un lapso de generación (la vida económica de la inversión).
³ Algunas características de las formas de estimación de la tasa de actualización con CAPM se resumen y comentan en Ekern (2007).
⁴ Terje Aven puntualiza: "El decididor sabe que esos juicios se basan en conocimiento y supuestos, y que son subjetivos en el sentido de que otros podrían llegar a conclusiones diferentes. Pero tales juicios se consideran valiosos si los analistas (y los expertos que intervienen en el análisis) tienen una sólida competencia en el campo relevante." (Aven, 2010a: 356).
⁵ En este contexto se suele usar la calificación de "aleatorio" en un sentido amplio, para referirse tanto a la incertidumbre originada en una variabilidad intrínseca (por ejemplo, la uniformidad de los productos que resultan del funcionamiento de una máquina) como a la incertidumbre de algo que no es suficientemente conocido (porque se refiere al futuro, o porque no se tiene conocimiento completo de algo presente). Esta última se suele denominar incertidumbre epistémica.
⁶ Hay varios programas para generar muestras aleatorias (como Crystal Ball, @Risk, Simul-ar, etc.). También se puede usar un programa para hacer el cálculo directamente con las distribuciones, sin requerir la simulación de un muestreo aleatorio.
⁷ Este aspecto es una diferencia con respecto a la estimación mediante números borrosos: esta metodología, en la forma en que se suele aplicar, equivale a la suposición probabilística de que las variables están totalmente correlacionadas. En caso de que la correlación sea menos que perfecta, la forma de la distribución puede ser más estrecha que la resultante de las estimaciones borrosas.
⁸ A partir del planteo de Bruno de Finetti (desarrollado en los años 1930), la probabilidad subjetiva se define operativamente como el precio de una apuesta de $ 1 sobre la magnitud de la variable. Esta interpretación de apuesta puede ser criticable cuando se considera un contexto en el que la estimación refleja el juicio de un analista, y no del decididor. Esto es así porque en esa interpretación se mezcla la información disponible con la actitud frente al dinero y la situación de apuesta, y se dice que la evaluación de riesgo debe separarse de cómo se valoran las consecuencias. Por eso, Terje Aven señala que sería necesario usar una palabra distinta a "subjetivo" para designar la evaluación probabilística del riesgo que está "basada en el conocimiento" disponible acerca de lo que se evalúa (Aven, 2010b).
⁹ La técnica de escenarios, como identificación de los "futuros posibles", se originó en los estudios de amplio alcance de Herman Kahn y después, desde los años 1960, fue usada en el planeamiento empresario en General Electric y Royal Dutch Shell. En este sentido, es diferente de la noción de "estados de la naturaleza", que se origina en la teoría formal de decisión para considerar la incertidumbre. En los dos ámbitos, cada uno por sus razones, existe la discusión acerca de si, y con qué alcance, puede hablarse de probabilidad de escenario (o de estado). Algunos comentarios pueden verse en Millett (2009) y Ha-Duong (2005).
¹⁰ Cuando, como ocurre generalmente, no se dispone del precio por peso del flujo de fondos para cada estado (según se comenta en el apéndice 1), la estimación de la distribución de probabilidad de los escenarios es una forma de estimar indirectamente esos precios para la valuación.
¹¹ Puede verse un resumen de estos métodos en van Leekwijck y Kerre (1999).
¹² El tratamiento de la correlación entre variables descriptas de modo borroso (con funciones de posibilidad), lo mismo que la correlación entre intervalos, ha sido planteado en fecha relativamente reciente. Puede verse Carlsson, Fullér y Majlender (2005).
¹³ La teoría de conjuntos borrosos planteada por Lotfi Zadeh desde 1965 (y la lógica borrosa como manifestación formal) se desarrolla para manipular formalmente de un modo más eficiente la imprecisión y la vaguedad del razonamiento humano que se expresa en lenguaje natural. Como señala Didier Dubois, "no es una teoría de la incertidumbre que desafía a la teoría de probabilidad; construir una teoría que reemplazara a ésta no estuvo nunca en la agenda de Zadeh."
¹⁴ "La lógica borrosa es la generalización de la lógica tradicional, y permite valores de verdad distintos que la verdad absoluta y la completa falsedad. Es apropiado decir que la lógica borrosa es comparable con la aritmética borrosa en el mismo sentido que la lógica es comparable con la aritmética; es decir, que no tienen mucho en común en términos de los tipos de problemas a los que pueden aplicarse." (Ferson, 2003)
¹⁵ La teoría de posibilidad (possibility theory) fue planteada por Lotfi Zadeh en 1978 (Zadeh, 1978) como una extensión de los conjuntos borrosos (fuzzy sets). Dubois y Prade (1988) desarrollaron una especificación compatible con un tratamiento cuantitativo en las decisiones, con medidas de posibilidad y de necesidad.
Posibilidad refleja la creencia de que ocurra un acontecimiento y necesidad se relaciona con la posibilidad de que no ocurra ese acontecimiento; la necesidad se define como el complemento a la unidad de la posibilidad de que no ocurra el acontecimiento. En general, la posibilidad de que ocurra un acontecimiento y la posibilidad de que no ocurra no necesariamente suman 1.
Posibilidad y necesidad, en un contexto de decisión, son medidas no aditivas que equivalen, respectivamente, a la plausibilidad y la credibilidad (belief) en la teoría de la evidencia (planteada por Arthur Dempster en 1967 y ampliada por Glenn Shafer), y a la probabilidad superior (upper probability) y la probabilidad inferior (lower probability) en la teoría de probabilidades imprecisas que formula Peter Walley en 1991.
La probabilidad inferior es el grado de confianza en que ocurrirá un acontecimiento, y la probabilidad superior es el grado en que preocupa que pueda ocurrir ese acontecimiento: la probabilidad superior de un acontecimiento está asociada con la probabilidad inferior de que no ocurra. En el lenguaje de la teoría de decisión y la interpreación como apuesta, la probabilidad (subjetiva) inferior sería un límite superior del precio que se considera para apostar a que ocurra el acontecimiento, y la probabilidad superior es el límite inferior del precio que se considera para apostar en contra de la ocurrencia del acontecimiento.
¹⁶ Estas dos categorías de incertidumbre tienen una extensa tradición en la teoría de probabilidad, ya que son las nociones de riesgo e incertidumbre extensamente consideradas por Frank Knight en 1921 (Knight, 1921). La probabilidad subjetiva es una forma de expresar la incertidumbre epistémica como grado de creencia (en condiciones de conocimiento incompleto).
Sin embargo, el conocimiento es parcial de muchas maneras: por falta de información relevante acerca del pasado, por el modelo con el que se interpreta la información para referirse al futuro, por la complejidad de la situación, por la imprecisión de las medidas de lo que se identifica. Puede verse un comentario de las consecuencias prácticas de las dimensiones de la incertidumbre en Rowe (1994).
¹⁷ Un resumen de estos aspectos puede verse en Dubois (2006).
¹⁸ Recientemente se ha suscitado un debate en torno a este tema, entre una perspectiva definidamente bayesiana para la evaluación de riesgo y las otras formas de operar con estimaciones que reflejan imprecisión. Puede verse Aven 2010a; Dubois (2010) y Huber (2010).
¹⁹ Por ejemplo, se han introducido distinciones para el tratamiento formal de las estimaciones realizadas mediante intervalos de confianza por uno o varios expertos. En el primer caso (un experto), se puede operar con esos intervalos mediante la aritmética borrosa, y en el segundo (varios expertos) debería operarse con la aritmética de intervalos aleatorios. Puede verse Baudrit y Dubois (2005).
También existen métodos para reunir, en la evaluación de riesgo, la información elaborada con forma probabilística y posibilística. Una explicación formal puede verse en Baudrit, Dubois y Guyonnet (2002).
²⁰ La estimación de la tasa de actualización con una distribución de probabilidad o un intervalo se considera en el punto 6, como base para una estimación congruente del valor en un rango o intervalo.
²¹ El valor que se calcula con los importes de máxima posibilidad del flujo de fondos borroso puede ser distinto al que se calcula con el valor esperado de distribuciones de probabilidad con forma similar, cuando los números borrosos y las distribuciones tienen una asimetría marcada. Pueden verse comentarios en Schjær-Jacobsen (2007).
²² Es necesario recordar que el cálculo de intervalos que se aplica para operar con números borrosos supone correlación perfecta; por tanto, para obtener resultados similares debe especificarse así en la simulación de Montecarlo. Como la correlación afecta relativamente poco a las medidas centrales (media, modo), el supuesto no tiene efectos muy grandes en el resultado. El grado de correlación influye en la amplitud de la distribución de probabilidad (o la amplitud del número borroso), y por eso puede afectar el juicio acerca del riesgo del flujo de fondos.
²³ La expresión de posibilidad, y no de probabilidad, de los escenarios que se consideran puede ser una forma adecuada para esta metodología de análisis aunque no se realicen estimaciones borrosas del flujo de fondos. Ha-Duong (2005) muestra la congruencia de esa expresión con el análisis de los "futuros posibles" de largo plazo, en comparación con las (formal aunque no semánticamente equivalentes) estimaciones de probabilidad.
²⁴ La amplitud del intervalo puede ser informativa, ya que tiene relación con la imprecisión de las estimaciones del flujo de fondos. Cabe mencionar que los resultados extremos ("peor" y "mejor") no son equivalentes a los escenarios extremos: en un caso se refieren a la amplitud de la estimación con una perspectiva de futuro, y en el otro a varias perspectivas de futuro. Por eso, en el caso de una perspectiva la valuación se realiza con el importe desborrosificado, y en el caso de escenarios con alguna forma de importe esperado (y no sólo con el escenario de máxima posibilidad).
²⁵ Los estudios acerca del efecto de la ambigüedad en la valoración de títulos se refieren a esa característica también como incertidumbre de modelo (model uncertainty) o incertidumbre knightiana (porque se considera una situación de desconocimiento de la distribución de probabilidad, tal como es la noción de incertidumbre que empleó Frank Knight en 1921).
El tema se ha planteado formalmente desde los años 1980, con diversos enfoques. Pueden verse comentarios en Kogan y Wang (2003); Epstein y Schneider (2008); Izhakian y Benninga (2011).
Un análisis del componente ambigüedad en el rendimiento del mercado en exceso de la tasa sin riesgo puede verse en Brenner y Izhakian (2011).
²⁶ Se puede explicitar la expresión analítica del valor esperado y la variabilidad del factor de actualización, a partir de los parámetros de la distribución de la tasa de actualización. Si bien la actualización con el valor esperado de la tasa, 1/E(k), no es igual a la actualización con el valor esperado del factor de actualización, E(1/k), para los niveles usuales de tasas la primera es una buena aproximación de la operación correcta. Puede verse Pérez Rodríguez (1997).
²⁷ Analíticamente, de un modo completo se puede trabajar considerando que la tasa es un proceso aleatorio. Sin embargo, tanto en condiciones de independencia como de correlación, es más práctico trabajar directamente con simulación, ya que el cálculo del valor de la inversión en forma analítica (con los dos primeros momentos de la distribución del valor, el valor esperado y el desvío estándar) es un poco complicado.
²⁸ Las probabilidades imprecisas se representan como límites de probabilidad (probability bounds, distribuciones superior e inferior denominadas P-boxes), intervalos de probabilidad, conjuntos aleatorios (random sets), nubes (clouds de Neumaier, que combina intervalos y distribuciones), o funciones de posibilidad.
Puede verse un resumen detallado en Dubois y Prade (2009), y un resumen más breve en Destercke, Dubois y Chojnacki (2007).
²⁹ Como se mencionó, la probabilidad subjetiva de un hecho se suele definir como el precio de una apuesta de $ 1 sobre la magnitud de la variable. Al considerar un intervalo de la probabilidad implica que hay un precio inferior (apostar a favor) y uno superior (apostar en contra) de esa magnitud, y dentro del intervalo hay indeterminación de la conducta (por imprecisión de la información). Esa definición de probabilidad subjetiva es, entonces, el caso de precio único (o precio "justo") de las apuestas a favor y en contra.
³⁰ Risk Calc es una herramienta que calcula analíticamente a partir de distribuciones únicas o con parámetros estimados en un rango, y permite considerar la correlación entre variables. Es una alternativa a la simulación aleatoria cuando no se dispone de datos en cantidad suficiente, o cuando deben reunirse estimaciones de expertos. Los detalles acerca del método pueden verse en Ferson, Kreinovich, Ginzburg, Myers y Sentz (2003). Puede verse una comparación de métodos en Ferson y Ginzburg (1996).
³¹ La estimación de la tasa como magnitud borrosa puede hacerse simplemente con estimaciones de los componentes CAPM con expresiones de intervalos o triangulares a partir de la información disponible.
Un modelo de estimación del rendimiento del mercado y del coeficiente beta a partir de estimaciones borrosas de expertos acerca de los rendimientos puede verse en Chrysafis (2012).
También puede operarse sobre la información de rendimientos de mercado con técnicas borrosas (por ejemplo, estimar un coeficiente beta borroso mediante regresión borrosa). Algunos comentarios del tema en Terceño, Barberà, Vigier y Laumann (2011).
³² Las pespectivas se analizan en Smith y Nau (1995) y Copeland y Antikarov (2001). Los enfoques para la valuación se resumen en Fornero (2004).
³³ Acerca de esto puede verse, por ejemplo, Götze, Northcott y Schuster (2008).
³⁴ Como se comenta en el punto 5, si la tasa se estima en un intervalo, o con una distribución de probabilidad, el valor que se calcula tiene una distribución (de probabilidad o de posibilidad). Los aspectos que se mencionan en este punto se refieren a la distribución del flujo de fondos en relación con el valor, y por eso son válidos para todas las formas de expresar la estimación de la tasa de actualización: puntual, probabilística, borrosa.
³⁵ Tal forma de valuar puede verse como una variante distorsionada de la aplicación a la valuación del enfoque media-varianza (o rendimiento-riesgo). En la evaluación de proyectos de inversión, este enfoque se basaría en la relación de rentabilidad y riesgo, considerando la tasa de rentabilidad de cada proyecto, y la estimación de valor resulta de una función de utilidad frente al riesgo. Sin embargo, la tasa interna de rentabilidad no es una rentabilidad de mercado, sino una rentabilidad sobre costo.
³⁶ Un comentario crítico del método de valor probabilístico y equivalente único se puede ver en Keeley y Westerfield (1972).
³⁷ Puede verse un resumen en Carmichael y Balatbat (2008). Cabe mencionar que el tratamiento analítico de la correlación (entre los componentes del flujo de fondos en cada período, y entre períodos) suele resultar en formulaciones bastante complicadas, aún realizando supuestos simplificadores. Los modelos formales se complicarían mucho más si se quiere obtener soluciones analíticas para las relaciones entre las variables primarias, que después se manifiestan en los componentes del flujo de fondos. Este ejercicio analítico-matemático puede evitarse con el uso de técnicas numéricas.
³⁸ Si bien en las formulaciones analíticas se refieren a la inversión inicial como el primer, y aparentemente único, importe negativo del flujo de fondos, la estimación borrosa que se plantea puede extenderse a un lapso mayor para los desembolsos de la inversión al comienzo del proyecto.
³⁹ Por ejemplo, hay estudios que consisten en determinar de modo analítico los equivalentes borrosos de los principales indicadores de una inversión (valor actual neto, tasa interna de rentabilidad, valor futuro neto, flujo anual equivalente, período de recuperación). Puede verse Kuchta (2000) y Kahraman, Ruan y Tolga (2002).
⁴⁰ Puede verse esta forma de cálculo en Durán y Milanesi (2009).
⁴¹ Para esto considera la probabilidad de cada escenario. Puede resultar curioso que, en un estudio que enfoca el tratamiento borroso de la estimación del flujo de fondos, se expresen los escenarios como una variable aleatoria. Tal como se comentó antes, este aspecto es el que parece quedar más adecuadamente descripto con una expresión de posibilidad más que de probabilidad. Sin embargo, una vez realizadas las estimaciones de posibilidad de escenarios, para realizar operaciones puede convertirse la distribución de posibilidad (no aditiva) en una distribución aditiva (que equivale a la expresión de una distribución de probabilidad).
⁴² Una evaluación de los resultados de diferentes métodos aplicables al ordenamiento de proyectos de inversión puede verse en Sorenson y Lavelle (2008).
⁴³ Chiu y Park (1994) proponen como base del ordenamiento de proyectos un indicador ponderado. Un valor como número borroso triangular (a, m, b) se resume con 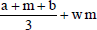, donde w es un coeficiente que se estima según la naturaleza y la magnitud del valor m de máxima posibilidad.
⁴⁴ Porque el razonamiento es presentado por Irving Fisher en The Theory of Interest (1930).
⁴⁵ Un título complejo es aquel que paga un importe distinto de cero al menos en dos estados; en este sentido, un título complejo (que es lo que habitualmente se valúa, bajo la forma de títulos en sí o negocios) es un conjunto de títulos puros.
Los títulos puros se denominan también títulos Arrow-Debreu, porque fueron planteados como encuadre general del reconocimiento del riesgo en las decisiones, en un contexto en el que los riesgos pueden transarse en los mercados financieros. Las referencias iniciales de este planteo son Arrow (1964) y Debreu (1959).
⁴⁶ El enfoque de preferencia tiempo-estado fue planteado por Jack Hirshleifer, sobre la base de los enunciados de Fisher y de las condiciones de Arrow y Debreu acerca de los mercados completos, como una teoría económica de la inversión en condiciones de incertidumbre. La extensión del enfoque se desarrolla en tres ensayos: Hirshleifer (1964, 1965, 1966).
Hirshleifer señala: "Al combinar el tratamiento de Fisher de las decisiones según las preferencias temporales en condiciones de certidumbre, con la concepción de Arrow de la elección en condiciones de incertidumbre, se tiene una teoría generalizada en la que los objetos de elección son oportunidades de consumo en fechas alternativas y en estados específicos del mundo (o, diremos, derechos alternativos tiempo-estado)." (Hirshleifer, 1964:80)
⁴⁷ Los primeros estudios en los que se plantea la estimación de los precios de los títulos puros a partir del precio de las opciones se publican en 1978: Breeden y Litzenberger (1978) y Banz y Miller (1978).
⁴⁸ Las nociones de riesgo con un precio en el mercado financiero y de riesgo privado, que no tiene un precio identificable en el mercado, se usa también para la valuación de la flexibilidad de los negocios. Puede verse una síntesis en Fornero (2004).

Bibliografía
1. Arrow, K. J. (1964). "The role of securities in the optimal allocation of risk-bearing", Review of Economic Studies, vol.31, n° 2, pp. 91-96 (versión en inglés del artículo presentado en International Colloquium on Econometrics, 1952, Le rôle des valeurs boursiéres pour la répartition la meilleure des risques)
2. Aven, T. (2010a). "On the need for restricting the probabilistic analysis in risk assessments to variability", Risk Analysis, vol. 30, n° 3, pp. 381-384.
3. Aven, T. (2010b). "Some reflections on uncertainty analysis and management", Reliability Engineering and System Safety, vol. 95, n° 3, pp. 195-201.
4. Banz, R. W. y Miller, M. H. (1978). "Prices for state-contingent claims: Some estimates and applications", Journal of Business, vol. 51, n° 4, pp. 653-672.
5. Baudrit, C. y Dubois, D. (2005). "Comparing methods for joint objective and subjective uncertainty propagation with an example in a risk assessment", 4^th International Symposium on Imprecise Probabilities and Their Applications.
6. Baudrit, C., Dubois, D. y Guyonnet, D. (2002). "Joint propagation and exploitation of probabilistic and possibilistic information in risk assessment", Journal of LATEX Class Files, vol. 1, n° 11, pp. 1-13.
7. Breeden, D. T. y Litzenberger, R.H. (1978). "Prices of state-contingent claims implicit in option prices", Journal of Business, vol. 34, n° 4, pp. 621-651.
8. Brenner, M. y Izhakian, Y. (2011). Asset prices and ambiguity, Working paper. Disponible en sitio web SSRN.
9. Carlsson, C., Fullér, R. y Majlender, P. (2005). "On possibilistic correlation", Fuzzy Sets and Systems, vol. 155, n° 3, pp. 425-445.
10. Carmichael, D.G. y Balatbat, M.(2008). "Probabilistic DCF analysis and capital budgeting and investment: A survey", The Engineering Economist, vol. 53, n°. 1, pp. 84-102.
11. Chiu, C-Y y Park, C.S. (1994). "Fuzzy cash flow analysis using present worth criterion", The Engineering Economist, vol. 39, n° 2, pp. 113-138.
12. Chrysafis, K. (2012). "Corporate investment appraisal with possibilistic CAPM", Mathematical and Computer Modelling, vol. 55, n° 3-4, pp. 1041-1050.
13.Copeland, T. y Antikarov, V. (2001). Real Options: A Practitioner's Guide, Texere.
14. Debreu, G. (1959). Theory of Value: An Axiomatic Analysis of Economic Equilibrium, Yale University Press.
15. Destercke, S., Dubois, D. y Chojnacki, E. (2007). "Relating practical representations of imprecise probabilities", 5^th International Symposium on Imprecise Probability: Theories and Applications, Prague, Czech Republic.
16. Dubois, D. (2006). "Possibility theory and statistical reasoning", Computational Statistics & Data Analysis, vol. 51, n° 1, pp. 47-69.
17. Dubois, D. (2010), "Representation, propagation, and decision issues in risk analysis under incomplete probabilistic information", Risk Analysis, vol. 30, n° 3, pp. 361-368.
18. Dubois, D. y Prade, H. (1988). Possibility Theory, Plenum Press, New York.
19. Dubois, D. y Prade, H. (2009). "Formal representations of uncertainty", en Bouyssou, D., Dubois, D., Pirlot, M. y Prade, H. (Ed), (2009). Decision-Making Process: Concepts and Methods, Wiley-ISTE. Disponible por separado en sitio web irit.fr/~Didier.Dubois.
20. Durán, R. y Milanesi, G. (2009). "Valuación de un activo biológico bajo la lógica fuzzy", International Association for Fuzzy Sets, XV SIGEF Congress: Economic and Financial Crisis: New Challenges and Perspectives, Lugo, Spain.
21. Ekern, S. (2007). "A dozen consistent CAPM-related valuation models: So why use an incorrect one?", Norwegian School of Economics and Business Administration (NHH) Working paper.
22. Epstein, L y Schneider, M. (2008). "Ambiguity, information quality, and asset pricing", Journal of Finance, vol. 63, n° 1, pp. 197-228.
23. Ferson, S. (2003). RAMAS Risc Calc 4.0. Disponible en www.ramas.com.
24. Ferson, S. y Ginzburg, L.R. (1996). "Different methods are needed to propágate ignorance and variability", Reliability Engineering and System Safety, vol. 54, n° 2, pp. 133-144.
25. Ferson, S., Kreinovich, V., Ginzburg, L., Myers, D.S. y Sentz, K. (2003). Constructing probability boxes and Dempster-Shafer structures, Technical report, Sandia National Laboratories. Disponible en sitio web personeel.ewi.tudelft.nl.
26. Fisher, I. (1930). The Theory of Interest: As determined by the impatience to spend income and opportunity to invest it, Macmillan, New York. Disponible en sitio web libertyfund.org.
27. Fornero, R.A. (2004). "Valor de las opciones reales, de los proyectos de inversión y de la empresa", Disertaciones XXIV Jornadas Nacionales de Administración Financiera, SADAF, Valle Hermoso, Córdoba, Argentina.
28. Götze, U., Northcott, D. y Schuster, P. (2008). Investment Appraisal, Springer.
29. Gutiérrez Betancur, J.C. (2006). "Aplicación de los conjuntos borrosos a las decisiones de inversión", Ad-minister Universidad EAFIT, n° 9, pp. 62-85.
30. Ha-Duong, M. (2005). "Scenarios, probability and possible futures", HAL-SHS (Hyper Article en Ligne-Sciences de l'Homme et de la Société). Disponible en sitio web halshs.archives-ouvertes.fr.
31. Hattis, D. y Burmaster, D. (1994). "Assessment of variability and uncertainty distributions for practical risk analyses", Risk Analysis, vol. 14, n° 5, pp. 713-730.
32. Hertz, D. (1964). Risk analysis in capital investment, Harvard Business Review, vol. 42, n° 1, pp. 95-106.
33. Hillier, F.S. (1963). "The derivation of probabilistic information for the evaluation of risky investments", Management Science, vol. 9, n° 3, pp. 443-457.
34. Hirshleifer, J. (1964). "Efficient allocation of capital in an uncertain world", American Economic Review, vol. 54, n° 3, pp. 77-85.
35. Hirshleifer, J. (1965). "Investment under uncertainty: Choice-theoretic approaches", Quarterly Journal of Economics, vol. 79, n° 4, pp. 509-536.
36. Hirshleifer, J. (1966). "Investment under uncertainty: Applications of the state-preference approach", Quarterly Journal of Economics, vol. 80, n° 2, pp. 252-277.
37. Hoffman, F.O. y Hammonds, J.S. (1994). "Propagation of uncertainty in risk assessments: The need to distinguish between uncertainty due to lack of knowledge and uncertainty due to variability", Risk Analysis, vol. 14, n° 5, pp. 707-712.
38. Huber, W. (2010). "Ignorance is not probability", Risk Analysis, vol. 30, n° 3, pp. 371-376.
39. Izhakian, Y. y Benninga, S. (2011). "The uncertainty premium in an ambiguous economy", Quarterly Journal of Finance, vol. 1, n° 2, pp. 323-354.
40. Kahraman, C., Ruan, D. y Tolga, E. (2002). "Capital budgeting techniques using discounted fuzzy versus probabilistic cash flows", Information Sciences, vol. 142, n° 1, pp. 57-76.
41. Kahraman, C. y Kaya, I. (2010). "Investment analyses using fuzzy probability concept", Technological and Economic Development of Economy, Baltic Journal of Sustainability, vol. 16, n° 1, pp. 43-57.
42. Keeley, R. y Westerfield, R. (1972). "A problem in probability distribution techniques for capital budgeting", Journal of Finance, vol. 27, n° 3, pp. 703-709.
43. Knight, F. (1921). Risk, Uncertainty and Profit, Houghton Mifflin, Boston. Disponible en sitio web econlib.org.
44. Kogan, L. y Wang, Tan (2003), "A simple theory of asset pricing under model uncertainty", Working paper. Disponible en sitio web haas.berkeley.edu.
45. Kreinovich, V., Beck, J., Ferregut, C.M., Sanchez, A., Keller, G.R., Averill, M.G. y Starks, S.A. (2004). "Monte-Carlo-type techniques for processing interval uncertainty, and their potential engineering applications", Proceedings of the Workshop on Reliable Engineering Computing. Disponible en sitio web savannah.gatech.edu. Publicado en Reliable Computing, vol. 13, n° 1, pp. 25-69, 2007.
46. Kuchta, D. (2000). "Fuzzy capital budgeting", Fuzzy Sets and Systems, vol. 111, n° 3, pp. 367-385.
47. Lin, S-C. y Lee, K-L. (2010). "Fuzzy investment decision based on economic and strategic factors: A case of air logistics service provider", African Journal of Business Management, vol. 4, pp. 2546-2553.
48. Millett, S.M. (2009). "Should probabilities be used with scenarios?", Journal of Futures Studies, vol. 13, n° 4, pp. 61-68.
49. Myers, S.C. (1968). "A time-state preference model of security valuation", Journal of Financial and Quantitative Analysis, vol. 3, n° 1, pp. 1-33.
50. Myers, S.C. y Turnbull, S. (1977). "Capital budgeting and the capital asset pricing model: Good news and bad news", Journal of Finance, vol. 32, n° 2, pp. 321-333.
51. Pérez Rodríguez, E. (1997). "Evaluación de proyectos cuando existe incertidumbre sobre los tipos de descuento", I Reunión Científica de Programación, Selección y Control de Proyectos, Almería, España.
52. Robichek, A.A. y Myers, S.C. (1965), "Conceptual problems in the use of risk adjusted discount rates", Journal of Finance, vol. 21, n° 4, pp. 727-730.
53. Rowe, W.D. (1994). "Understanding uncertainty", Risk Analysis, vol. 14, n° 5, pp. 743-750.
54. Samuelson, P.A. y Merton, R.C. (1969). "A complete model of warrant pricing that maximizes utility", Industrial Management Review, vol. 10, n° 2, pp. 17-46.
55. Schjær-Jacobsen, H. (2007), "Numerical modeling of economic uncertainty", Journal of Industrial Engineering International, vol.3, n° 5, pp. 9-18.
56. Sevastjanov, P., Dimova, L. y Sevastianov, D. (2006). "Fuzzy capital budgeting: Investment project evaluation and optimization", Studies in Fuzziness and Soft Computing, 201, pp. 205-228.
57. Smith, J.E. y Nau, R.F. (1995). "Valuing risky projects: Option pricing theory and decision analysis", Management Science, vol. 41, n° 5, pp. 795-816.
58. Sorenson, G.E. y Lavelle, J.P. (2008). "A comparison of fuzzy set and probabilistic paradigms for ranking vague economic investment information using a present worth criterion", The Engineering Economist, vol. 53, n° 1, pp. 42-67.
59. Terceño, A., Barberà, G., Vigier, H. y Laumann, Y. (2011). "Coeficiente beta en sectores del mercado español: Regresión borrosa vs regresión ordinaria", Cuadernos del CIMBAGE, n° 13, pp. 79-105.
60. Tsao, C-T. (2005). "Assessing the probabilistic fuzzy net present value for a capital investment choice using fuzzy arithmetic", Journal of the Chinese Institute of Industrial Engineers, vol. 22, n° 2, pp. 106-118.
61. Tsao, C-T. (2012). "Fuzzy net present values for capital investments in an uncertain environment", Computers & Operations Research, vol. 39, n° 8, pp. 1885-1892.
62. van Leekwijck, W. y Kerre, E.E. (1999). "Defuzzification: Criteria and classification", Fuzzy Sets and Systems, vol. 108, n° 2, 159-178.
63. Yao, J-S., Chen, M-S. y Lin, H-W. (2005). "Valuation by using a fuzzy discounted cash flow model", Expert Systems with Applications, vol. 28, n° 2, pp. 209-222.
64. Zadeh, L. (1978). "Fuzzy sets as a basis for a theory of possibility", Fuzzy Sets and Systems, vol.1, nª 1, pp. 3-28.