Services on Demand
Article
Estudios Económicos
On-line version ISSN 2525-1295
Estud. Econ. vol.32 no.65 Bahía Blanca July 2015
Let it float: new empirical evidence on de facto exchange rate regimes and growth in Latin America
Cecilia Bermúdez* - Carlos Dabús*
* CONICET e Instituto de Investigaciones Económicas y Sociales del Sur. E-mail: cdabus@criba.edu.ar, cbermudez@uns.edu.ar
enviado: julio 2015
aceptado: septiembre 2015
Resumen
El trabajo reconsidera la evidencia encontrada por Levy-Yeyati y Sturzenegger (LYS) (2003) sobre la relación entre regímenes cambiarios y crecimiento económico. Utilizamos su clasificación de facto así como su base de datos, a fin de ganar robustez y eficiencia en los resultados. Aplicamos el método System GMM. Además, el trabajo se realiza para una amplia muestra de países así como para el caso de Latinoamérica para el periodo 1974-2004. A diferencia de LYS, nuestra evidencia indica que los regímenes cambiarios no son significativos para explicar el crecimiento económico, tanto para una amplia muestra de países como para Latinoamérica en particular. Sin embargo, en esta región los regímenes flexibles parecen tener más ventajas en términos del rol de los determinantes del crecimiento económico en relación a los otros regímenes cambiarios.
Código JEL: O00, E00, F31.
Palabras clave: Regímenes Cambiarios; Crecimiento Económico; System GMM.
Abstract
This paper reassesses the evidence presented in Levy-Yeyati and Sturzenegger (LYS) (2003) on the relation between exchange rate regimes and economic growth. We use their de facto classification as well as their database, in order to gain robustness and efficiency in the results. We run System GMM estimations. Additionally, we focus on Latin American countries for the period 1974-2004. Differently to LYS, our evidence indicates that exchange rate regimes are not significant to explain economic growth, both in a worldwide sample of countries and particularly in Latin America. However, in this region flexible regimes appear to have more advantages in terms of the role of the determinants of economic growth in relation to the other exchange regimes.
JEL Code: E00, F 31, O00.
Keywords: Exchange Rate Regimes; Economic Growth; System GMM.
INTRODUCTION
The relation between exchange rate regimes and economic growth is a relevant and controversial issue in macroeconomics. Nevertheless, and despite a large literature on the subject, it is not clear which regime is more favorable to growth. Empirical evidence shows two main results. First, hard pegs have declined in its relevance; policymakers have made more emphasis on stabilizing the real economy. In second place, fix (flex) exchange rate regimes are associated to lower (higher) inflation and higher (lower) output variability1. Levy Yeyati and Sturzenegger (LYS) (2003) suggest that the combination of lack of exchange rate adjustments under a peg and nominal rigidities result in price distortions and higher output volatility in the event of real shocks. In turn, in presence of open capital markets an exchange-rate target results in the loss of independent monetary policy, and so in the inability to respond to shocks, which again promotes economic fluctuations.
On the other hand, fix regimes act as a nominal anchor that, by providing credibility to monetary policy ensures long run price stability and predictability both by restraining money growth and by enhancing money demand. As suggested by Bordo and Schwartz (1999), historical evidence shows that the convertible regime was one of fixed exchange rates and a stable nominal anchor. Stability, however, came at the expense of great exposure to foreign shocks. In presence of wage and price stickiness, these shocks again could produce volatile output and employment.
On the contrary, a flexible exchange rate regime is better suited for insulating the economy against such shocks, so that economic fluctuations should be (and in fact they are) a less serious problem. Mussa (1986), Baxter and Stockman (1989), Ghosh et al. (1997), Bordo and Schwartz (1999) and Broda (2001) present a large amount of evidence supporting this view. According to Bailliu et al. (2003), in presence of monetary rigidities in goods and labor markets, flexible regimes can easily absorb economic shocks because when the exchange rate is allowed to fluctuate, the real economy can escape from the shock consequences. Thus, more flexibility should contribute to lower output variability. In turn, a more flexible exchange rate regime is less likely to generate persistent misalignments in exchange markets, which result in economic crisis. In both cases one might expect lower economic fluctuations. However, empirical evidence shows that more flexible exchange rates are associated to higher inflation2. In such cases there is no nominal anchor, so that policymakers can use monetary and fiscal policy tools to avoid negative effects of external or internal shocks on the level of economic activity and employment.
In short, the advantages of less (more) flexible exchange rate arrangements are price (in) stability, while the costs are higher (lower) output variability. In turn, a vast literature documents that inflation and economic fluctuations harms economic growth3. Therefore, the natural question that arises is whether the benefits of a more flexible system outweigh their costs, so that this can be preferred to a fix one to foster economic growth.
This topic has become popular in the literature, particularly since the development of different de facto methodologies for classifying exchange rate regimes. The growing interest in assessing the impact of different exchange rates regimes on economic growth stems mainly from the fact that the empirical research based on the de jure classification (the exchange rate regime officially declared by central banks to the IMF) shows quite unsatisfactory results, as there is no consensus about whether exchange rates affects key real macroeconomic variables, or if it does, through which channels.
In particular, empirical evidence is not unambiguous about what regime is better to stimulate economic growth. Mundell (1995) compares the industrial economies for the previous and subsequent periods to the demise of Bretton Woods, and finds faster economic growth in the former. Mac Donald (2000) suggests that fixed exchange rate arrangements within the euro-zone area are likely to stimulate a good economic performance, since this system "...squeezes out the negative effects of exchange rate volatility on trade and investment" [Mac Donald (2000), p. 49]. Nonetheless, Ghosh et al. (1997), using the de jure IMF classification, do not find a clear relation between exchange rate regimes and growth, while Ghosh et al. (2000) show that currency boards are associated to higher economic growth.
Alternatively, other empirical studies suggest that flexible regimes favors economic growth. Rolnick and Weber (1997), using long-term data for 15 economies, present evidence that output and inflation grow faster under fiat than under commodity standards. In addition, recent empirical evidence suggests that the results differ for industrial and developing countries. Larrain and Velazco (2000) conclude that flexible regimes are recommended for developing countries, because the pressure brought by massive capital flow reversals and weakened domestic financial systems was too much to bear, even for countries that followed reasonably sound macro policies and had seemingly plentiful reserves. Indeed, they argue that there exists what some analysts have termed "the law of the excluded middle": there is apparently no intermediate exchange rate regime suitable for emerging markets, as large swings in capital flows would make them vulnerable to speculative currency attacks (Eichengreen, 1994; Fischer, 2001).
However, by using different de facto classifications, the literature has moved significantly forward in recent years, shedding light into the benefits of intermediate exchange rate regimes in developing countries. Ghosh et al. (1997) find that certain countries with regimes officially reported as pegs, often undergo frequent devaluations in order to maintain or enhance competitiveness. Conversely, Calvo and Reinhart (2002) focus on a group of countries with regimes classified as flexible under the de jure classification, and find that this economies exhibit what they have called 'fear of floating': in countries with a high degree of financial dollarization, the monetary authority has strong incentives to intervene in the exchange market to reduce exchange rate volatility.
Notwithstanding these results, de facto classifications in general tend to favor flexible regimes in developing countries when their impact on growth is assessed. In this sense, one pioneer and most salient of the empirical works on this issue is LYS (2003), who construct a de facto methodology for classifying exchange rate regimes and show that, for a sample of 154 countries over the post-Bretton Woods period (1974-1999), there is a positive and strong link between floating regimes and economic growth in non-industrial countries, but this relation is weak for industrial economies.
However, their results rely heavily on the econometric method chosen for estimating the relation between exchange rates and growth. Consequently, and taking into account the developments in the econometric field since LYS work, an interesting question that arises is whether their results hold when using, for instance, Arellano-Bond estimators. The intuition is that more efficient methods that rule out endogeneity could weaken the relationship between growth and exchange rate regimes.
In that sense, the purpose of this paper is twofold. A first goal consists of re-estimating two of LYS's models by using System GMM. We use their open-access database that has been recently updated to the year 2004, while the country dataset is kept the same. A second goal is to focus on Latin American countries. First, we run a System GMM introducing LYS dummies for the exchange rate regime. Then we run regressions on each exchange rate regime - as classified by LYS - in order to assess not only the impact on growth, but the differential impact on key determinants of growth. This could lead to interesting results, as the exchange rate might have an indirect effect on economic growth which is not captured when using dummies as regressors in a panel data model.
The next section presents the data and the estimation methodology. In section II we present and analyze the regression results, jointly with the usual post-estimation tests. Section III presents the evidence of the relation between exchange rate regimes and economic growth for the particular case of Latin America. Finally, we present the conclusions..
I. METHODOLOGY
LYS (2003) present three estimations of the relationship between de facto exchange rate regimes and economic growth: a panel based on five-year averages, a second one with annual observations for the whole sample period (1976-2000), and finally cross country growth á la Barro regressions. Although the authors have made a great contribution in the development and use of a new exchange rate regimes database, their work presents at least two problems: the first one is a methodological issue. The authors acknowledge that endogeneity may be a problem, and growth may in turn have an impact on the exchange rate regime choice. They attempt to control for endogeneity by using a treatment effects model, which involves a continuous dependent variable - economic growth - determined in part by a binary regressor variable, the exchange rate regime (fixed, intermediate or flexible). Since the dummy might be endogenous, the treatment effects method has two stages. In the first, the dummy is regressed on a set of instruments in a probit and logit regression. In the second, the fitted values from this first model are employed as instruments in the growth equation. Theoretically, this technique controls for the simultaneity of the exchange rate regime. However, Angrist and Krueger (2001) find that using a nonlinear first stage to generate fitted values for a second stage regression results in inconsistent estimates if the nonlinear model is not exactly right.
In order to overcome this first issue, we run estimates on both panels (annual and averaged observations) using System GMM approach developed by Arellano and Bover (1995) and Blundell and Bond (1998)4. This estimator combines the first-differenced GMM approach, which uses lagged independent variables as instruments in the levels equations to deal with possible endogeneity issues in the regressors, with the original equations in levels, thus increasing the efficiency of the estimators when the series are persistent. Therefore, their lagged levels are only weakly correlated with subsequent first-differences (Blundell and Bond, 1998). Finally, the estimation of growth models using the system-GMM estimator for linear panel data has now become standard in the literature (see Beck, 2008).
II. EMPIRICAL EVIDENCE
In this section we present the empirical evidence on the relation between exchange rate regimes and economic growth for both LYS (2003) and our estimations, which were carried out by means of System GMM and by using LYS database. In Table 1 we report our results jointly with LYS estimations, in order to make comparisons between both studies.
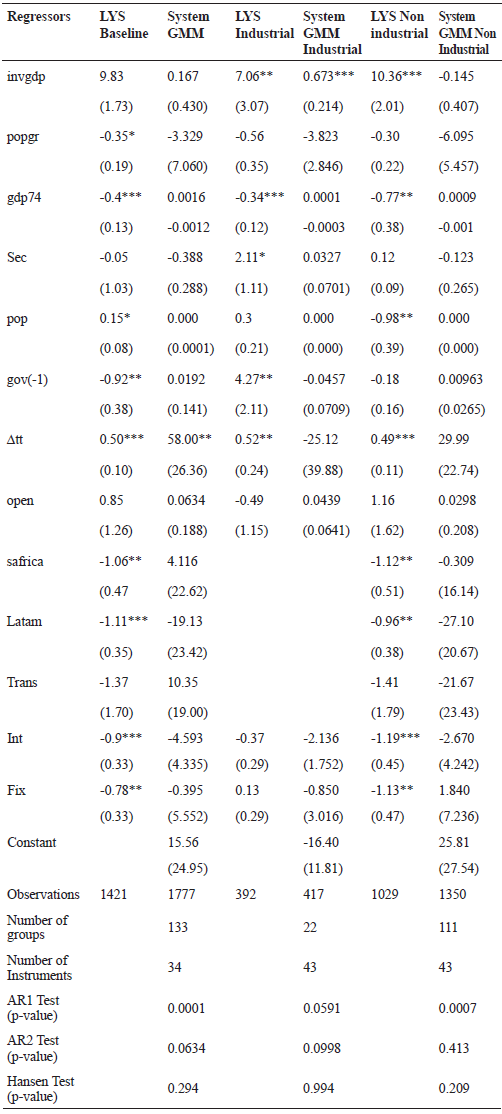
Table 1. Growth Regressions (Annual Data)
Standard errors in parentheses. *** p<0.01, ** p<0.05, * p<0.1
As it can be seen the control variables behave in different ways. There are only two variables that have a similar behavior: real per capita growth is positively correlated with the investment-to-GDP ratio (INVGDP), even though in our case we find that this relationship is significant only for industrial countries. The rate of change of the terms of trade (?TT) is also positively correlated with growth, and in both LYS all-country estimations and our results the coefficient is significant. However, we do not find differences between industrial and non industrial countries.
Contrary to LYS findings, in our estimations initial per capita GDP (GDP74), computed as the average over the period 1970-1973, does not indicate the presence of conditional convergence. Similarly, we do not found significant secondary enrollment (SEC), population growth (POPGR), openness (OPEN), the growth rate of government consumption (GOV(-1)) and the regional dummies (Sub-Saharan Africa (SAFRICA), Latin America (LATAM) and transition economies (TRANS)).
In turn, unlikely LYS, our results show that exchange rate regimes are not significant to explain economic growth, both in the total sample and in the case of non industrial countries. This important difference can be based in the fact that we carry out the regressions by using GMM methodology, which in fact is a more robust way to deal with endogeneity that the instrumental variables used by LYS.
On the other hand, the lack of significance of almost all the control variables may be related to the use of annual data. LYS argue that, since exchange rate regimes "change rapidly over time, longer-term classification may be less informative" than using the annual frequency [LYS (2003), p. 1181)]. However, this could cause some specifications problems: while the exchange rate index (which differentiates fix, float and intermediate regimes) is compiled annually, it is not at all usual to have regressions for long-term growth done with annual data. As the authors recognize, there is a large literature on the short-run effect of exchange rates on economic growth, which is why we are thus inclined to find the results of the five-years average regressions more reliable. In this model, the dependent variable is the average growth rate of per-capita GDP in five-year increments over the period 1974-2004. The regressors are the same as in the annual data panel, but here the authors add the variable LYSAVG. This is computed in base on the classification developed by LYS. If a country was classified as floating in a given year, the index equals zero. If the currency regime was intermediate, the value is one, and if exchange rates were fixed, the value is two. The average of the index for the five-year periods over the years available from 1974-2004 is then taken and used as the regressor for the currency regime. Both LYS and our estimation results, which were carried out with five-year average data, are presented in the following table.
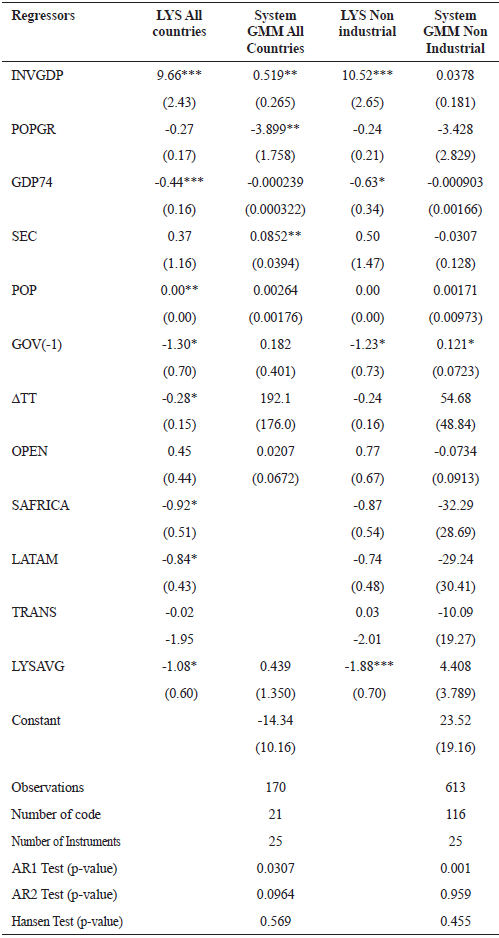
Table 2. Growth Regressions (Five Year Averages)
Standard errors in parentheses. *** p<0.01, ** p<0.05, * p<0.1
The interpretation of these results is not straightforward. As it can be seen, the results differ from those obtained when using annual data, and only the ratio of investment seems to be robust to both specifications. Also, Table 2 shows that, unlikely LYS, the variable LYSAVG is not significant in our regressions. This difference can have two explanations. First, this can be due to the fact that this variable is constructed as an average of index numbers that go from 1 to 3, as the regime approaches a hard peg. However, it should be taken into account that averaging the regimes implies that there is a linear relationship between them, and thus an "intermediate" regime is in the exact middle of the other extremes. This assumption, of course, affects the relationship between the variable LYSAVG and economic growth, and could be the reason why we cannot find it significant in our regressions.
On the other hand, the other problem with LYS results is associated with the meaning of the de facto fixed exchange rate. Every regime is associated with other economic policies, some of which are hard to observe. For instance, a de facto floating regime might be a result (and a condition) of an inflation targeting scheme, as movements in the interest rate are determined by the central bank. In turn, a de facto fixed regime might be a consequence of a heavily intervened exchange rate market, and not necessarily a stable hard peg. Thus, LYS estimations might not be able to determine whether an exchange rate regime truly exerts an independent effect on growth. In order to overcome this issue, the authors add other control variables, as inflation and some dummies for banking and currency crises, and find that, while the coefficients are slightly lower, fixed rates still exert a significant, negative impact on growth. In a similar line, Miles (2006) creates an interaction variable with LYSAVG and a black market premium index, and finds that LYSAVG is not significant, while the interaction term becomes negative and significant at 5% level.
III. THE CASE OF LATIN AMERICA
In this section we estimate the "exchange rate regimes-economic growth" for Latin America because of three reasons. First, we want to carry out a deeper analysis of the relationship in a developing economies region relatively homogeneous. Secondly, LYS find that the effect of the exchange rate regime is significant only in non-industrial countries, so that we want to explore if this result remains in this particular region. Finally, much of the literature on the de facto classifications of exchange rate regimes are mostly based on panel data estimations for Asian economies, while there are only a few cases of studies for Brazil and Mexico. Our proposal makes an attempt to fill this gap in the literature by analyzing the impact of de facto exchange rate regimes - as classified by LYS - in Latin America. Also here we propose a System GMM estimation of a parsimonious growth model following Bermúdez et al. (2012), where the explanatory variables include those found robust by Levine and Renelt (1992) -gross investment as a share of GDP and the exports plus imports ratio to GDP-, the GDP per capita growth rate lagged one period, and two instability measures: the inflation rate and the volatility of GDP growth rate. Both variables are unambiguously related to one or another exchange rate regime. As it was mentioned above, a floating regime should be able to absorb shocks, while it is associated with the risk of a higher inflation. Contrarily, a peg should help to maintain low levels of inflation, but could be severely affected by external shocks.
In Table 3 we report the results. The first column shows the results of a System GMM estimation for the entire dataset of Latin American countries, during the period 1974-2004, using LYS binary dummies to capture the exchange rate regime. The next three columns report GMM estimation results for each regime - using LYS classification - which allow us to have a better interpretation of the behavior of each regressor in each regime, and not only the impact on economic growth.
Table 3. Growth Regressions in Latin America
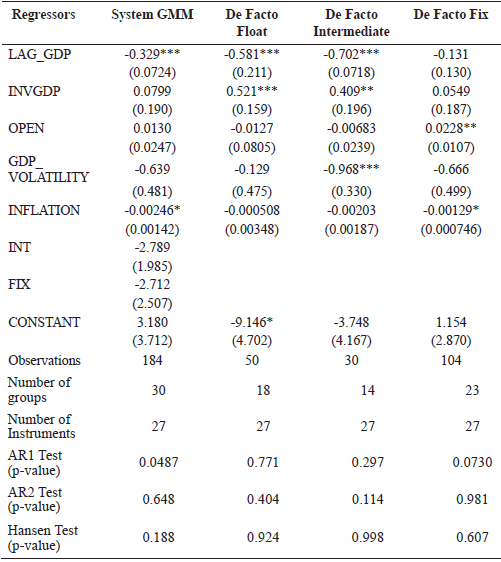
Standard errors in parentheses. *** p<0.01, ** p<0.05, * p<0.1
As it can be seen in Table 3, the inflation rate is significant for the whole sample, but the regime seems to have no effect on the economic performance of the region. However, when dividing the sample by regime, we find quite interesting results: the ratio of investment to GDP is positive and significant both in floating and intermediate regimes; in turn, the ratio of exports plus imports to GDP (OPEN) is positive and significant when there is an operating peg. Surprisingly, inflation affects negatively economic growth in fixed regimes, while it is not significant in floating and intermediate regimes. This result requires a careful interpretation. One explanation for this finding can be that, as fixed regimes have often followed periods of great inflation, the disinflation process is made under the fixed regime. In turn, contrarily to the intuition, GDP volatility does not impact negatively on growth under pegs. In fact, the economic performance is more affected by shocks when there is an intermediate exchange rate regime in operation. Besides, it is worth noting that under a floating regime the economic performance of the region is neither negatively affected by GDP volatility nor inflation. Moreover, the coefficient of the ratio of investment to GDP is significant and quite high, in relation to the intermediate regime.
While these results are not conclusive, they provide insightful information about a central topic in macroeconomics which is still controversial, and of particular importance to Latin American economies. Our estimations show that while the exchange rate regime might not have a straight impact on economic growth, this does not mean that the regime does not matter. On the contrary, we show that every regime has indeed a differential impact on key determinants of growth. In particular, a floating regime seems to have a better performance than the others in terms of its capacity to cope with instability, and its positive association with investment.
CONCLUSIONS
This paper re-estimated the LYS's model about the relationship between exchange rate regimes and economic growth by using System GMM. In first place, this used their open-access database that has been recently updated to the year 2004, while the country dataset was kept the same. Secondly, it focused in the particular case of Latin American countries. To do that, we run a System GMM introducing LYS dummies for the exchange rate regimes, and then we run regressions on each regimes - as classified by LYS - in order to assess not only their impact on growth, but also the differential impact of other key determinants of economic growth.
As in the case of the global sample as in the particular case of Latin America, in line with Miles (2006), our results differ with LYS evidence. In particular, in relation to the "exchange rate regimes-economic growth" relationship, our results show that exchange regimes, and in special the flexible arrangements, are not significant to explain economic growth in non industrial and Latin American countries. Therefore, the results are sensible because of two main reasons. First, when using annual data the cycle effect is present in the estimation results. Second, System GMM is a more robust methodology to deal with endogeneity, so that some significant effects of exchange rate regimes on economic growth disappear when this is applied. Besides, in the particular case of Latin America, in the case of regressions by regimes, the flexible exchange rate regime seems some advantages in relation to the other regimes. In particular, investment is positive and significant to explain economic growth, while instability variables are not significant, so that the growth explanatory variables seem to behave in the expected way in the case of flexible regimes.
Finally, a possible extension of this work can be to replicate the LYS model estimation with System GMM to other developing regions, in order to determine if the lack of robustness of the results found here is a general problem or a particular feature of Latin America in the case of the relation between exchange rate regimes and economic growth.
Notas
1 See Bordo and Scharwtz (1999) for an extensive treatment of the relation between exchange rate regimes and economic performance. They analyze international evidence in the framework of four regimes: the classical gold standard (1880-1914), the interwar period in which a short-lived restoration of the gold standard prevailed, the postwar Bretton Woods system (1946-1971), and the more recent managed float period (1971-1995). In these periods the evidence shows that high inflation is associated to flex exchange rate regimes, and output variability arise in gold standard and convertibility rule periods. Other studies that compares historical regimes performance are Meltzer (1986), Mills and Wood (1993), and Ghosh et al. (1996).
2 See Bordo and Schwartz (1999) and references there.
3 Evidence of the negative "inflation-economic growth" relation can be found in De Gregorio (1992), Barro (1997) and references there, while the negative effect of economic cycles and growth has been documented by Ramey and Ramey (1995).
4 We did not include the variable CIVIL, which stands for "civil rights", as the Freedom House website cited in LYS's work does not have enough information to run GMM estimations, as most of the countries in the sample have indexes only for the last decade. Also, we decided to include a constant term in order to help us check for omitted variables.
BIBLIOGRAPHY
1. Angrist, J., & Krueger, A. (2001). Instrumental variables and the search for identification: from supply and demand to natural experiments, Journal of Economic Perspectives, 15 (4), 69-85.
2. Arellano, M., & Bond, S. (1991). Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations, Review of Economic Studies, 58, 277-297.
3. Arellano, M., Bover, O. (1995). Another look at the instrumental variable estimation of error-components models, Journal of Econometrics, 68 (1), 29-51.
4. Bailliu, J., Lafrance, R., & Perrault, J. (2003). Does exchange rate policy matter for growth? International Finance, 6 (3), 381-414.
5. Barro, R., (1997). Determinants of economic growth: a cross-country empirical study, Cambridge, MA: MIT Press.
6. Baxter, M., & Stockman, A. (1989). Business cycles and the exchange-rate regime: some international evidence, Journal of Monetary Economics, 23, 377-400.
7. Beck, T. (2008). The econometrics of finance and growth, World Bank Policy Research, Working Paper Series No. 4608.
8. Bermúdez, C., Dabús, C., & González, G. (2012): Inestabilidad y crecimiento económico: evidencia de América Latina. En S. N. Keifman. Progresos en Crecimiento Económico (pp. 117-165), Ciudad Autónoma de Buenos Aires: Fondo Editorial Consejo.
9. Blundell, R., & Bond, S. (1998). Initial conditions and moment restrictions in dynamic panel-data models, Journal of Econometrics, 87 (1), 115-143
10. Bordo, M., & Schwartz, A. (1999). Monetary policy regimes and economic perfomance: the historical record. In Handbook of Macroeconomics Vol. 1A (pp. 149-234). Amsterdam: Elsevier.
11. Broda, C. (2001). Coping with terms-of-trade shocks: peg versus floats. American Economic Review, 91 (2), 376-380.
12. Calvo, G., & Reinhart, C. (2002). Fear of floating, Quarterly Journal of Economics, 117 (2), 379-408.
13. Cooper, R., Dornbusch, R., & Hall, R. (1982). The gold standard: historical facts and future prospects, Brooking Papers on Economic Activity, 1982, 1-56.
14. De Gregorio, José (1992): The effects of inflation on economic growth: Lessons from Latin America, European Economic Review, 36 (2-3), 417-425.
15. Eichengreen, B., Rose A., & Wyplosz, C. (1994). Speculative attacks on pegged exchange rate: an empirical exploration with special reference to the European Monetary System, NBER, Working Paper No. 4898.
16. Fischer, S. (2001). Exchange rate regimes: is the bipolar view correct?, Journal of Economic Perspectives, 15 (2), 3-24.
17. Ghosh, A., Gulde, A., Ostry, J. & Wolf, H. (1996). Does the exchange rate regime matter for inflation and economic growth?, Economic Issues, 2, Washington, D.C., International Monetary Fund.
18. Ghosh, A., Gulde, A., Ostry, J., & Wolf, H. (1997). Does the nominal exchange rate regime matter?. NBER, Working Paper Series No. 5874.
19. Ghosh, A., Gulde, A. & Wolf, H. (2000). Currency boards: more than a quick fix?, Economic Policy, 15 (31), 269-335.
20. Larraín, F. & Velasco., A. (2001). Exchange rate policy in emerging market economies: the case for floating. Princeton University, Essays in International Economics No. 224.
21. Levine, R., & Renelt, D., (1992). A sensitivity analysis of cross -country regressions, American Economic Review, 82 (4), 942-63.
22. Levy-Yeyati, E., & Sturzenegger, F. (2003). To float or to fix: evidence on the impact of exchange rate regimes on growth. American Economic Review, 93 (4), 1173-1193.
23. Mac Donald, R., (2000). The role of the exchange rate in economic growth: a Euro-zone perspective. National Bank of Belgium, Working Papers Research Series No. 9.
24. Meltzer (1986). Some evidence on the comparative uncertainty under different monetary regimes. In C.D. Campbell and W.R. Dougan (Eds.). Alternative Monetary Regimes. (pp. 122-153). Baltimore M.D.: John Hopkins University Press.
25. Miles, W. (2006). To float or not to float? Currency regimes and growth. Journal of Economic Development, 31 (2), 91-105.
26. Mills, T., & Wood G., (1993). Does the exchange rate regime affect the economy?. Federal Reserve Bank of St. Louis Review 75 (4), 3-20.
27. Mundell, R., (1995). Exchange rate systems and economic growth. In M. C. Marcuzzo, L. H. Officer, & A. Rosselli (Eds.). Monetary Standars and Exchange Rate. (pp. 13-38). London: Routledge.
28. Mussa, M., (1986). Nominal exchange rate regimes and the behavior of real exchange rates: evidence and implications. Carnegie-Rochester Conference Series on Public Policy, 25, 117-214.
29. Ramey, G., & Ramey, V., (1995). Cross-country evidence on the link between volatility and growth. American Economic Review, 85 (5), 1138-1151.
30. Rolnick, A., & Weber. W. (1997). Money, inflation, and output under fiat and commodity standards. Journal of Political Economy, 105 (6), 1308-1321.
© 2015 por los autores; licencia otorgada a la Revista Estudios Económicos. Este artículo es de acceso abierto y distribuido bajo los términos y condiciones de una licencia Atribución-No Comercial 3.0 Unported (CC BY-NC 3.0) de Creative Commons. Para ver una copia de esta licencia, visite http://creativecommons.org/licenses/by-nc/3.0/